以前、宇宙の「浮舟」のページで円制限三体問題を数値計算しましたが、その方法について解説しておきます。
三つの天体が互いに万有引力を及ぼしあいながら運動している系の振る舞い、いわゆる三体問題は解析的には解けず、数値計算で解くしかありません。三体問題のうち、第三の天体の質量μが、第一、第二の天体の質量Mおよびmに比べ、極めて小さい場合を制限三体問題と言います。制限三体問題では第一、第二の天体の運動は第三の天体の運動に影響を及ぼすが、第三の天体の運動が第一、第二の運動に影響することはないと仮定します。
例えば、地球と月と宇宙船からなる系では、宇宙船は、地球と月がつくる場の中を、両者から影響を受けながら、運動しますが、宇宙船は地球や月に比べ極めて軽いので、逆に宇宙船の運動が、地球や月の運動に影響を及ぼすことはないとします。
さらに、第一、第二の天体がその共通重心の周りに円運動をしているとき、円制限三体問題と言います。地球、月、宇宙船の例なら、地球と月の間の距離が一定であれば、円制限三体問題となります。円制限三体問題も、一般の三体問題と同じく解析的には解けないので、一般にはこの場合も数値計算で解くしかありません。
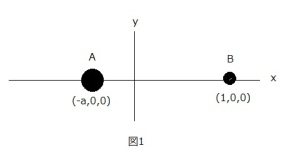
図1のように、互いに一定距離を保ちながら運動する二つの天体、つまり、質点A(質量M)と質点B(質量m)からなる系を考えましょう。質点AとBは系の重心を中心して、ともに同じ角速度で一定平面上を円運動していますので、座標系として、重心を原点として、AやBの公転の角速度と同じ角速度で回転する回転座標系に乗って見れば、AとBは静止していることになります。
長さの単位として、原点OからBまでの距離を選び、その長さを1としましょう。原点からAまでの距離をαとすると、原点が重心だから、
 となります。
となります。
ここで、Ω=1になるように、つまり、公転周期が2πになるように、時間の単位を選ぶと、(4)および(5)より、それぞれ、
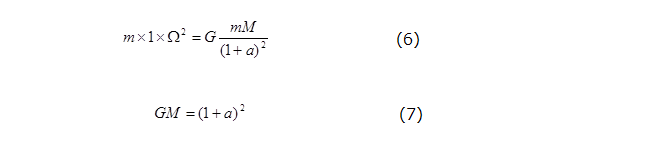
となり、当然、(6)、(7)は(2)を満たします。
次に、この回転座標系のなかでの、第三の天体である小質点の運動を考えてみましょう。但し、その質量μ は、A、Bの質量に比べ、極めて小さく、その存在は、A,Bの運動に影響を及ぼさないものとします。小質点は次のⅰ)~ⅳ)の4つの力を受けながら、回転座標系の上を運動することになります。
ⅰ)質点Aから受ける万有引力FA
ⅱ)質点Bから受ける万有引力FB
ⅲ)座標系が回転していることによる遠心力FO
ⅳ)コリオリの力FC
小質点の質量μは運動方程式のなかには入ってこないので、始めからμ=1とおいて構いません。力のx,y,z成分をそれぞれ、X,Y,Z とする。座標(x,y,z)にいる小質点にAが及ぼす力FAの成分XA、 YA 、YAはそれぞれ、
同様に、力FB の成分は
となります。
さらに、遠心力FO およびコリオリの力FC については
となるので、小質点の運動方程式は
と表わされます。
(20)~(22)は2次の連立微分方程式になっていますが、これに適当な初期条件を与えて数式ソフトを用いて計算すれば、小質点の軌跡が描かれます。
小質点に働く力のうち、コリオリの力以外はポテンシャルであらわすことができます。それぞれの力に対応するポテンシャルは
であり、全ポテンシャルUはU=UA+UB+UO です。小質点はこのポテンシャル場のなかをコリオリの力を受けて運動しますが、小質点が回転座標系から見て、その一点 に静止しているとき、小質点はコリオリの力は受けないので、小質点に働く力が釣り合うところは、ポテンシャルの勾配がゼロ、つまり、gradU=0 が成り立つ場所であります。力の釣り合い点はxy面上にしかないので、xy面上の等ポテンシャル線から力の働かない平衡点を探すことができます。
運動方程式(20)~(22)も、ポテンシャルの式(23)~(24)も、円制限三体問題では、系を特徴づけるパラメーターは第一と第二の質点の質量比αのみとなります。αの値を適当に選ぶことによって、第一および第二の天体を、太陽と木星に選んだ場合、太陽と地球に選んだ場合、あるいは地球と月に選んだ場合の小天体の運動が数値計算できます。
まず、ポテンシャルの式を用いると、ラグランジュポイントの位置が計算できます。次に運動方程式に、初期条件を入れると、パソコンが小天体の軌道を計算して図にえがいてくれます。初期条件を設定する際には、長さの単位として、原点から天体Bまでの長さを1に選んだことと、公転周期を2πに選んでいることを考慮して決めます。
宇宙の浮舟のページで紹介した計算結果はMATEMATICAという計算ソフトを使って計算したものです。プログラムは、マニュアルの例題を見ながら作れば簡単です。数式を書き下すのとほとんど同じなので、少々面倒ではありますが、高校の物理の知識があればできるでしょう。但しこのソフトは、購入するのに高価なのが難点です。
円制限三体問題
 未分類
未分類
コメント