成虫では冬を越せない蝶などの昆虫は卵の状態で冬を越すため、異なる世代が重なることはありません。ある年、n年のその昆虫の個体数をXnとすると、Xnはその前年の個体数Xn-1で決まると考えるのが妥当でしょう。つまり、XnはXn-1の関数として、
Xn=f(Xn-1) (1)
のように表されると考えられます。関数f(X)と基準の年、0年の個体数X0 が与えられれば、(1)式をn=1として、X0の値を右辺に代入すれば、X1 が決まり、X1が決まれば、同様に(1)式をn=2として、これから X2が決まるというように、次々に決まり、任意の整数nに対して Xnが求まることになります。
f(X)=aX(1-X)の場合を考えてみましょう。つまり、(1)式を次のようにしましょう。
Xn=aXn-1(1-Xn-1) (2)
nに関係なくXnが正の数であるためには、X0が0より大きく、1より小さくなければなりません。さらにX1も0より大きく、1より小さくなければなりませんので、パラメータaは0より大きくて4より小さくなければなりません。
(2)式を計算するには電卓でもできますが、エクセルを使えば、簡単に計算できる上に、その結果を一瞬にしてグラフに描いてくれます。
私もエクセルには不慣れですが、一緒に計算エクセルを開いて計算してみましょう。例えば、aの値が0.9、初期値が0.6の場合を計算してみます。セルA1をアクティブにして、そこに「=0.6」と書き込みます。次にセルA2をアクティブにして、そこに、「=0.9*A1*(1-A1)」と書き込み、Enterキーを押します。この状態ではセルA1には、「0.6」セルA2には「0.216」の数字が入っています。さらに、セルA2をアクティブにし、セルの右下の+を下に適当なところまでドラッグしますと、セルA3以下のセルに数字が入りますが、これは、例えば、A6では、「=0.9*A5*(1-A5)」を計算したことになっています。これを棒グラフにすると、図1のようなグラフが得られます。この場合、単調減少となりますが、初期値X0を変えてA1を0.2としてもグラフの変化の様子は単調減少であることに変わりありません。
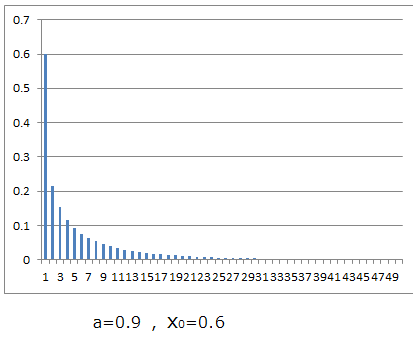
図1
次にこの数列を図形的に作図する方法について述べます。図1‘のように、xy座標系に、グラフy=x(これをグラフ①とします)とグラフy=0.9x(1-x) (これをグラフ②)を描きます。X0=0.6ですからx軸上の0.6からy軸に平行な直線を引き、これとグラフ②の交点のy座標の値がX1の値となりますので、その交点から、今度はx軸に平行に直線を引き、それが①と交わる交点のx座標がX1となります。X1が分かると同様な繰り返しをしてX2がわかり、図形的に次々と数列の項を求めることができま、この場合は0に収束する数列になることが直感的にわかります。
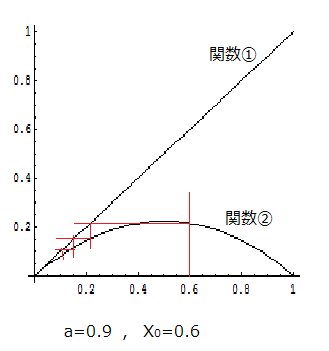
図1‘
次に(2)式を用いて、いろんなaの値に対して、同様な計算をしてみましょう。aを1.8として、セルA1に入れる初期値X0を0.2としてみましょう。今度は図2のように、単調増加しながら一定値に近づくことが分ります。その様子は初期値を変えても変わりません。
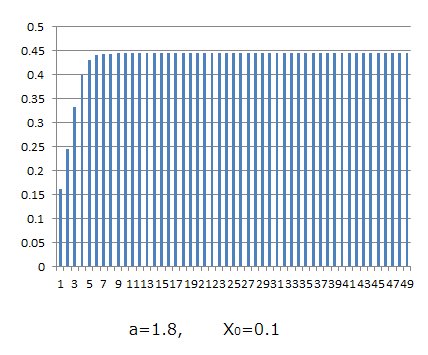
図2
この場合も図形的に求めると、図2‘のようになります。今度の場合、数列はグラフ①とグラフ②の交点に収束することが分かります。
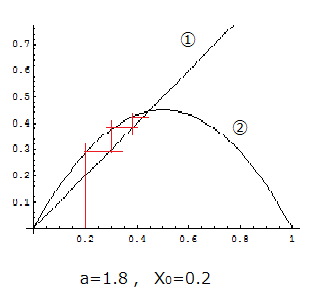
図2‘
さらに、a=3.3 ,X0=0.1 として計算すると、図3および図3‘
のように、一年ごとに、大小二つの値を交互にとることになります。つまり、最終的には、図3‘の赤い四角の太線に沿って巡ることになります。これは昆虫なら、多い年と少ない年とが、農産物なら豊作と凶作の年とが交互にやってくることに対応しているでしょう。
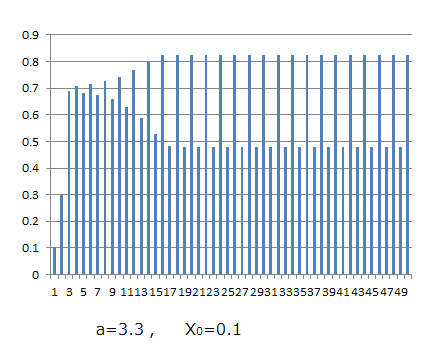
図3
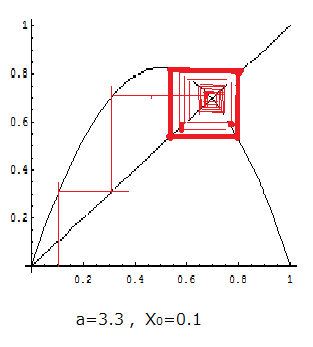
図3‘
今度はa=3.5としてしましょう。初期条件は適当にX0=0.2とでもしておきましょう。次のような結果が得られます。
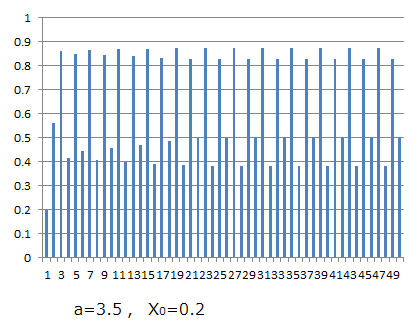
図4
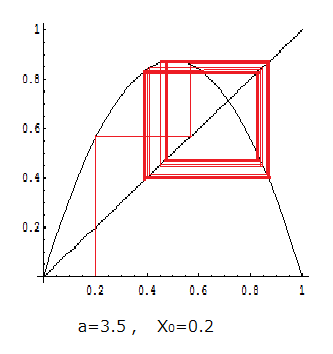
図4‘
図4または図4‘から、この場合には最終的には4年周期になることが分かります。
ここまでは数列は規則的な変化をしましたが、今度はa=3.8とし、初期値を0.6およびそれと僅か0.1%に異なる0.6006に選んでみましょう。この場合はXの変化は、これまでとは、一変し、それぞれ図5の上図および下図のようになります。
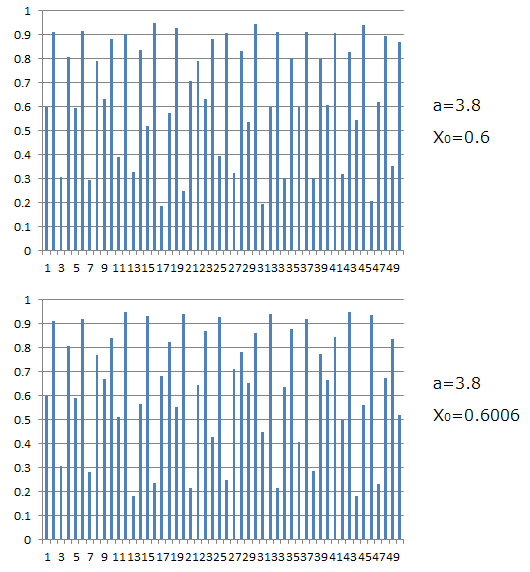
図5
一定の規則で計算したにも関わらず、この場合は不規則な変化をしています。図5の上下の両図はaの値が同じなので、まったく同じ規則で計算されていますが、初期値X0だけがほんのわずか0.1%だけ異なっています。上下両図のXnの値を比較すると、nが小さいうちは、ほぼ同じ値ですが、nが大きくなると、両者の違いが次第に大きくなります。つまり、両者の初期値の違いがnが大きくなるにつれ増幅され、やがて、両者は似ても似つかぬ変化をすることになります。このような現象をカオスと呼ばれています。
この計算では(2)式で表わされる規則を用いましたが、なぜ(2)なのかという疑問を持たれることでしょう。これは既に複雑系の数理1でお話ししたロデイステイック方程式を差文化したものが(2)式になるからです。ロデイステイック方程式そのものは特に変わったふるまうはしませんが、これを差文分化すると、その振る舞いは図5の場合のように、パラメータの値によってはカオスが現れることになります。
ここで、台所の水道の蛇口を使って、カオスの実験をしてみましょう。まず、蛇口をひねると、蛇口から水柱となって水が流れでますが、流れ出る水の量は時間に比例するでしょう。しかし、蛇口をだんだん絞っていくと水柱は細くなり、流れ出る水の量も少なくなります。しかし、さらに絞ると、水は水柱を作ることができず、水滴となって落ちてきます。このとき、水滴が落ちる時間間隔に注目して下さい。蛇口を絞りすぎると等間隔で落ちますが、適当に絞ると、「ポタリ、ポタ、ポタ、ポトリ」というように間隔が不規則になることがあります。その場合にも、水滴の落下は、重力と表面張力によって支配されているのですが、蛇口からの水の出を、連続から不連続にすることでカオスが現れたのです。
しかし、カオスは連続な変化にも現れます。例として、天気図を考えてみましょう。当然、天気図は連続的に変化しますが、今日のある時刻での天気図が分かると、それと似た過去の同じ季節、同じ時刻の天気図を探し出して比較すれば、1時間後も、また、明日や明後日の天気図がどうなるかは予測できるでしょう。1週間もなんとか予測できるでしょう。しかし、図5の上下の図で、nが増すにつれ、その違いが増大するように、1カ月後の天気の予測はできないでしょう。
今回、エクセルを用いて、(2)式の計算を行いましたが、いろいろなaの値について、計算すると、その解は、aの値の範囲によって、次のようなふるまいをすることが分かります。
0より大きく、1より小さいとき:単調減少し、0に収束する。
1より大きく、2より小さいとき:単調に増加しながら一定値に収束する
2より大きく、3より小さいとき:減衰振動しながら一定値に収束する
3より大きく、3.57より小さいとき:偶数周期の周期的変化
3.57より大きく、4より小さいとき:カオス
一定の規則によって変化するにも関わらず、予測できないもの、それがカオスです。
複雑系の数理3
 未分類
未分類
コメント