筆者が大学受験の頃、ある大学の過去問に、次のような数学Ⅲの面白い問題があった。まともに解こうとすれば、かなり面倒だが、これにカヴァリエリの定理が使えることに気づけば、実に簡単に解けるのである。センター試験も共通一次もなかった半世紀以上昔のことだが、その問題を紹介しておこう。
問題:変数と
が
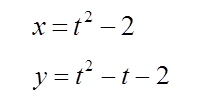
のようにパラメーター表示されている。と
の関係を表わすグラフと
軸とで囲まれる部分の面積を求めよ。
この問題にカヴァリエリの定理をどう使うのか、えっ!もう分かった?!それならあなたは天才かも知れない!しかし、まず、この問題を、よけいなことは考えず、決まり切った通常の方法で解いてみよう。
几帳面な人の解法
与えられた二つの式からtを消去し、と
の関係式を求めると、
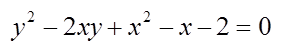
となる。変数をパラメータとする、
についての二次方程式とみなし、解の公式を用いて解くと、二つの解、y+(x)およびy–(x)が、xの関数として次のように与えられる。
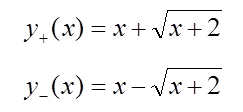
上の二つの関数を図示すれば、
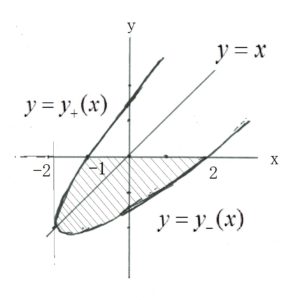
となり、斜線の部分の面積を求めればよいことが分かる。よつて求める面積Sは
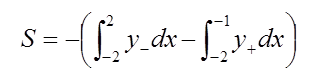
となる。あとは間違えないように計算して答をだせば完璧である。しかし、この問題を受験ということから離れて考えれば、無精者の筆者にとって、上記の解法には不満が残る。ルート記号が入った関数を積分するのは面倒だし、間違いやすい。さらに、欲を言えば、数学は美しく、そこには感動がなければならない。かく言う筆者は大学受験で1浪したので、受験生にはあまり勧められないが、上のグラフの図を見ていると別の解法が浮かんでくる。
カヴァリエリの定理
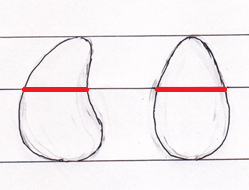
カヴァリエリの定理は、当時の数Ⅲの教科書の最後に付録として載っていた。下の図のように、二つの平面図形が、平行な二本の直線に挟まれているとき、その二本の直線に平行に引いた任意の直線の図形で切り取られる部分(赤色の部分)の長さが、二つの図形で等しいとき、二つの図形の面積は等しい。 この定理をさきほどの問題に適用してみよう。
無精もんの解法
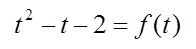
とすると、であり、
であるから、求めるグラフは
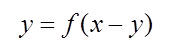
と表され、さらに

となる。これは二つグラフと
をx方向に加えたものである。後者のグラフは
であるから、問題の図形は、下図のように、簡単な二次式、
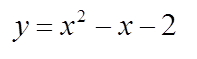
を表わす図形上の点(x,y)をx方向にyだけ平行移動して得られる図形である。
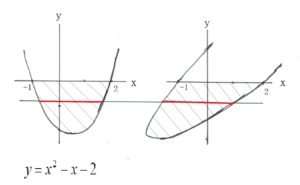
よつて、カヴァリエリの定理から、上の左右両図の斜線部の面積は等しい。求める面積は

となり、初歩的な積分の問題となる。これなら計算間違いすることもなかろう。

真っ直ぐ積んで 千円ならば
横にずれても 同じ千円!
Eureka!
それでは、もうひとつ問題を
閉曲線 の概形は?そして閉曲線で囲まれる面積はいくら?

コメント
[…] 参考 カバリエリの定理 […]