
(1)式で表わされる積分値Iを求めるには、次の(2)式で表わされる二重積分を考えます。
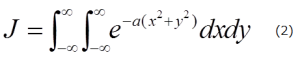
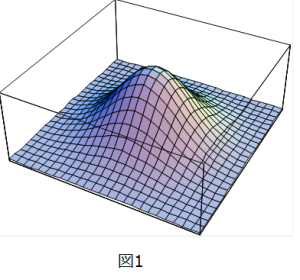
(2)式の被積分関数は、xおよびyの関数であり、その関数値をzとして、図示すると、図1のように、z軸のまわりに回転対称の「山」の形をした図形となります。これは計算ソフトのマテマチカを用いて描いたものです。無限に広がる裾野を持つこの「山」の体積が、Jの値になります。山の体積を二通りの方法で計算してみましょう。
〇第1の方法
図1の山を食パンに見立てて薄切りにしてみましょう。図2のように、食パンのy軸に垂直に包丁を入れると、切り口はxz面となりパンの断面のグラフは、y=一定として、式(3)で表され、これをxで積分すると、その断面積が(4)で表されます。
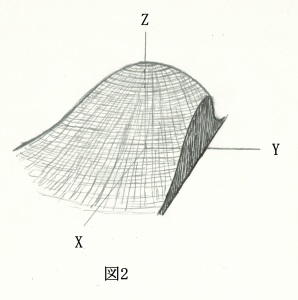
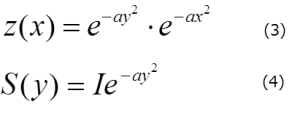
さらに、(4)式で表される断面積を厚さ方向yで積分すると、図1で表されるパンの体積Jが、
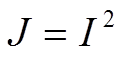
となります。
〇第2の方法
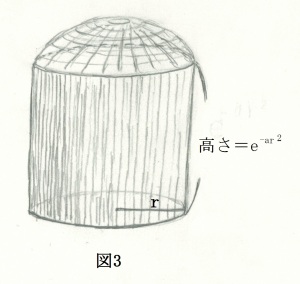 次に、食パンに、図3のように半径rの円筒形の包丁で切れ目をいれると、切り口の側面積は、円周の長さ×高さですから、次の(5)式のように表されます。
次に、食パンに、図3のように半径rの円筒形の包丁で切れ目をいれると、切り口の側面積は、円周の長さ×高さですから、次の(5)式のように表されます。
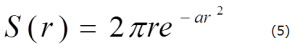
この側面積をrで0から∞まで積分してもJの値を求めることができ、
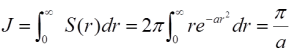
となります。
これと第一の方法での結果とから、
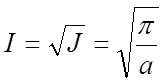
となります。つまり、ガウス積分は
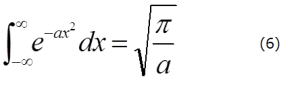
となります。
以上のようにしてガウス積分の値が求まりましたが、(6)式の両辺をaの関数とみなして、aで1回、2回と微分すると、
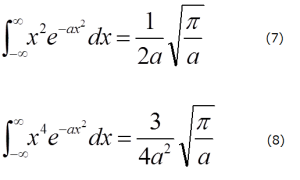
となります。
また、
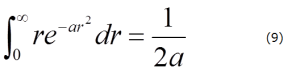
となりますから、これも、aで1回2回と微分すると、
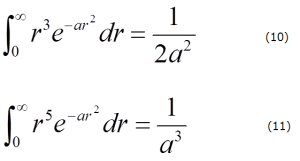
となります。
尚、(6)、(7)、(8)は被積分関数はxの偶関数で、積分範囲は-∞から∞までですが、(9)、(10)、(11)の被積分関数はrの機関数で積分範囲は0から∞であることに注意してください。
問題 図1の食パンの体積を計算するのに、第1の方法はy軸に垂直な平面で切り、第二の方法は円筒形の包丁で切りましたが、第3の方法として、z軸に垂直な平面で薄い円板に切り分けて積分すればどうなるでしょうか。
解答
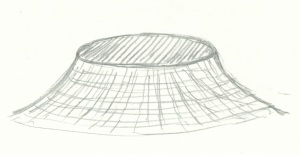
z軸に垂直な平面;z=一定(0<z<1)で切ると切り口の断面は円となり、その半径をrとすれば、exp[-ar2]=z 。よつて、切り口の断面積S(z)=πr2=-(π/a)logzとなり、これを積分すると、部分積分を用いると「食パン」の体積が次のように求まる。

ガウス関数の積分
 大学院入試過去問
大学院入試過去問
コメント