垂直に固定されている壁に向かって一定の速度-vで水平に進んできた球が弾性衝突し、衝突後向きを変え、速度vで離れ去った。球が壁に触れた瞬間、つまり衝突が始まった瞬間の時刻を、衝突が進行し、球の重心が一瞬静止した時刻を
、球が向きを変え、衝突が終了した瞬間の時刻を
とする、球と壁とが接触している間に、球が壁から受ける力をRとする。図1は弾性体の壁に剛体球が衝突した場合であり、図2は剛体の壁に弾性体球が衝突した場合の衝突途中の図である。
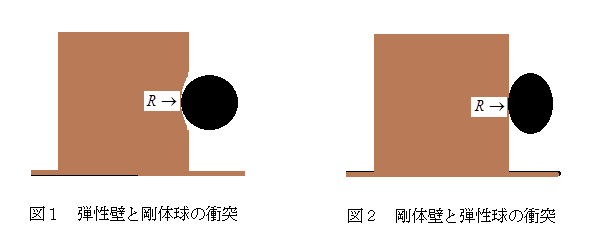 球の質量をMとし、右を正の向きとすると、図1と図2のどちらの場合も球は負の運動量-Mvとそれに相当する運動エネルギーを持って壁に近づくが、衝突が始まると、力Rの力積によって、負の運動量の球に正の運動量が加わりはじめ、時刻
球の質量をMとし、右を正の向きとすると、図1と図2のどちらの場合も球は負の運動量-Mvとそれに相当する運動エネルギーを持って壁に近づくが、衝突が始まると、力Rの力積によって、負の運動量の球に正の運動量が加わりはじめ、時刻で球の運動量は0となり、球は一瞬静止する。その後、球の運動量は正となり、時刻
まで増え続け、最終的にはMvとなる。図1と図2では、壁が変形するかしないかの違いだけであり、運動量については同じである。しかし、衝突が起きている間のエネルギーについては、壁が変形するかしないかで大きく異なる。
図1の場合、衝突の前半では球が壁に負の方向の力-Rを及ぼすことによって壁に仕事をし、壁は変形エネルギーを増し、球は運動エネルギーを失う。衝突後半では壁が球に正方向の力Rを及ぼし球に仕事をする。壁は前半でエネルギーを蓄え、後半で使用している。これに対して、図2の場合、壁は変形しないので、エネルギーを蓄えることができない。力Rは壁からの抗力となるが、正負同時一対の仕事なら、壁はエネルギーを蓄えることができなくても、抗力Rによつて球に仕事をすることができる。図2の衝突前半ではRは重心運動に負の仕事をすると同時に球の変形運動に正の仕事をし、衝突後半では、逆に重心運動に正の仕事をし、変形運動に負の仕事をしている。
壁と球との弾性衝突
 未分類
未分類
コメント