1.はじめに
日本物理教育学会の会誌の表紙に、なぜか高校数学で習う三角関数の和と積の公式が描かれている(図1)。三角関数の和積の公式と呼ばれる高校生にはお馴染みの式だが、それが物理教育とどう関係しているだろうか。
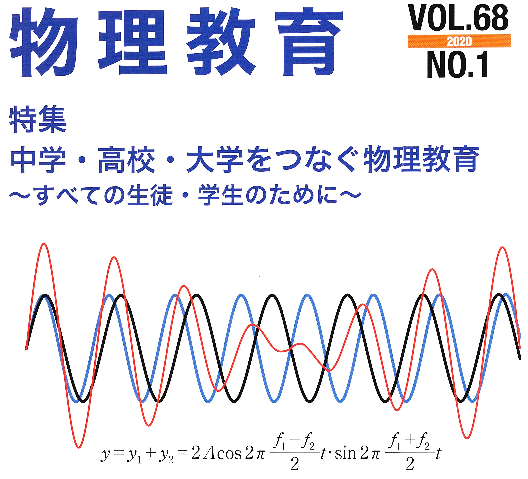
振幅が等しく振動数の僅かに異なる二つの波や振動を重ね合わせるとき、三角関数の和積の公式を図示すると、図1の赤い曲線で表される振幅変調された波が得られるが、これをよく見ると、振幅が0になった瞬間、位相が反転していることが分かる。位相の反転は振幅の符号の反転だから、それが振幅0のとき起きるのは当然のことだが、位相の反転は連成振動にとって重要であり、連成振動間のエネルギーの流れを反転させる。
2. バネと重りによる連成振動
いろいろな連成振動が考えられるが、まず、数学的な扱いが簡単な、バネ係数がKのバネ2個とバネ係数がkのバネ1個、質量がmの2個のおもりAとBを図2のように組み合わせた連成振動を考えてみよう。ただし、中央のバネのバネ係数kは左右のバネ係数Kに比べ小さく、おもりに働く摩擦はないとする。
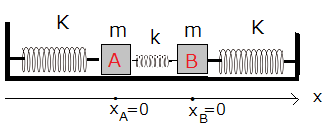
二つのおもりAおよびBの座標をそれぞれxAおよびxBとし、二つのおもりがつりあって静止している位置を、それぞれ、xA=0およびxB=0に選ぶ。さらに、つり合いの状態では、三つのバネはどれも伸び縮みのない自然長であるとする。AとBがつり合いのを位置から、それぞれ、xAおよびxBだけ変位したとき、三つのバネは自然長から、それぞれ、左のバネはxAだけ伸び、右バネはxBだけ縮み、中央のバネはxB–xAだけ伸びる。よつて、おもりAおよびBの運動方程式は次のように表せる。
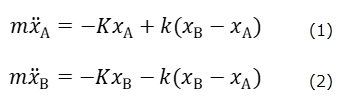
(1)と(2)は連立方程式であるが、ここで、変数変換をして、xB+xA=x+ 、xB–xA=xー とすると、(1)+(2)および(2)-(1)から、次の2式で表される単振動に分離できる。。
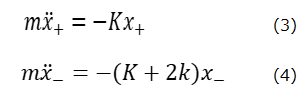
方程式(3)で表される振動は、おもりAとBとが一定の距離を保ったまま同位相で振動し、中央のバネは伸び縮みしない。一方、方程式(4)で表される単振動は、AとBとが逆位相、つまり、位相差180°で振動するので、AとBは左右対称の振動をする。(4)では、中央のバネも伸び縮みし、運動方程式はKとkの両方に依存する。(4)式の右辺のバネ定数が、K+2kになるのは、左右対称の振動だから、中央のバネの中心は固定されているのと同じであり、バネの長さが半分になると、バネ定数は2倍になることを示している。(3)と(4)式で表される単振動が系の固有振動である。振動数は前者より後者のほうがわずかに大きくなる。そこで簡単のため、(3)式の振動の角振動数をωーε、(4)式の振動の角振動数をω+εとする。
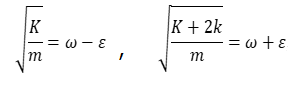
t=0で二つの固有振動の位相差が0であったとすると、二つの固有振動の式は次のように表される。
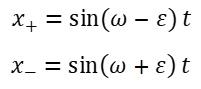
一般には、振動は、二つの固有振動x+とx-の重ね合わせで表すことができ、αx++βx-、または、αx+-βx-となる。α=β=1/2の場合を考えると、重ね合わされた二つの振動は、xA=(x+ーx-)/2 、xB=(x++xー)/2となり、前者は(1)式の解、後者は(2)式の解となる。さらに、三角関数の差および和の公式から、重りA及びBの変位、xAおよびxBは次の式ように振動する。
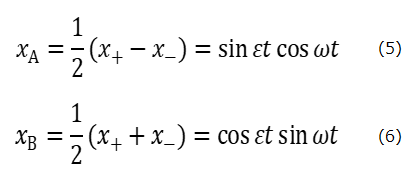
(5)式をsinεtで振幅変調された、角振動数ωの余弦振動、(6)式をcosεtで振幅変調された角振動数ωの正弦振動と見なすことができる。0<εt<90°では(5)の振幅は増加し、(6)の振幅は減少する。その間の(5)と(6)振動の位相は(6)式の位相が(5)の位相より、90°先行しているので、運動エネルギーが、重りBから重りAに移動するため、Aの振動が増幅し、Bの振動は減衰する。εt=90°になると、Aの振動の振幅が最大となり、Bの振動の振幅cosεtは正から負に反転する。それは振動sinωtの位相が180°変わることを意味しその結果、(6)式の振動の位相は(5)式の振動より90°遅れ、エネルギーの流れも逆転しAからBへとエネルギーの流れの向きが変化する。
3. 連成振り子
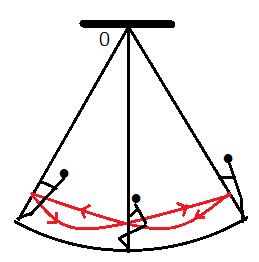
図3のように、長さが等しい二つの振り子AとBからなる連成振り子では、AとBとの間でエネルギーが交換される。振り子A、Bが鉛直となす角度を、それぞれ、θA、θBとして、振り子Bのおもりだけを手で支え、初期状態を、θA=0、θB=θ0とし、AとBがともに静止した状態から、振り子Bを初速度0で振らせると、AはBに位相が90°遅れて振れるので、エネルギーがBからAに向かって移動する。Aの振れは大きくなり、Bの振れは減衰する。やがて、Aの振幅が最大値θ0、Bの振幅が0となるとその瞬間、Bの位相が180°反転する。そのため、今度はAの位相がBの位相より90°だけ先行し、エネルギーの流れの向きがAからBに変化する。
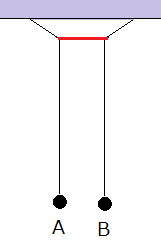
二つの振り子を同位相または逆位相で同じ振幅で振らせると、エネルギーの移動は起こらず、二つの振り子が一定の振幅を保ったまま振れ、そのときの二つの振動は固有振動である。振動数は、同位相の固有振動よりも逆位相の固有振動が僅かだけ大きくなる。位相差90°の振動は二つの固有振動を重ね合わせた振動であり、振動数が僅かにことなるため、振り子の振動にうなりが生じる。
図2のバネと重りからなる系では、おもりの間でのエネルギーのやり取りには二つのおもりを繋ぐ中央のバネがその役割を果たすが、図2の連成振り子ではAとBの振動を繋ぐ図中の赤い糸の張力が図1の中央のバネと同じ役割をしている。振り子の振れ角θの正弦が、sinθ≒θと近似できる範囲であれば、図3の運動は図2の運動に対応させることができる。二つの固有振動が混じった振動では、図2の真ん中のバネや図3の赤い糸の張力が二つのおもりの一方の振動に負の仕事をし、他方の運動に正の仕事をすることによってエネルギーを受け渡ししている。
4. 位相の反転の力学的および数学的意味
図2の振動も図3の振り子の振動も、二つの同じ振動子AとBが相互作用しながら連成振動をするとき、二つの振動子の振動は振幅変調された(5)式と(6)式で表され、両者の振動はどちらかが90°だけ先行している。先行していた振動がエネルギーを使い果たし、振動が静止した瞬間、その振動の位相が反転するため、今度は90°遅れることになる。つまり、振動子が静止し位相が反転するごとにエネルギーの移動の向きが逆転する。
5. バネ付き振り子

図5のように、糸とバネと五円硬貨の重りでバネ付き振り子を作製した。天井の定点から糸を吊るし、釣り合って静止している状態から、重りを下方に手で引っ張って放し、重りを上下に振動させると、重りは上下方向に一定の振幅で振動した。
次に、糸の長さを変化させながら同じ実験を行うと、ある適当な長さでは、重りの上下振動が減衰しながら、かわりに重りは振り子のように横揺れを始めた。その後、バネの伸縮振動と振り子の揺れ振動の二つの振動が交互に生じる。一方の振動が最大になり、他方の振動が止まると、止まった振動の位相が反転し、それにつれ最大になっていた振動が減衰を始める。図2や図3の連成振動では、相互作用により同じ二つの振動子の間でエネルギーが交互に行き来したが、今度はバネの伸縮振動と振り子の揺れ振動との間でエネルギーが交互に行き来する。
二つの振動子の間でエネルギーの移動が生じるためには、振動子間の相互作用が必要であるが、図1では、真ん中のバネがその役目をし、図2では二つの振り子を結ぶ横糸の張力がその役目をし、バネ付き振り子ではバネと重りを繋ぐ部分の張力、つまりはバネを吊るしている糸の張力が相互作用の役目をしている。バネ付き振り子を吊るした糸の張力は、バネの伸縮運動と振り子の揺れ振動の一方に負の仕事をし他方に正の仕事をする。
6.ブランコの原理
バネ付き振り子の連成振動を、ブランコの原理を説明するのに使えないだろうか。人がブランコに乗って横揺れがない状態から屈伸運動をして、その重心を上下に、ある一定の周期で振動させると、バネ付き振り子と同じく、図6のようにブランコに横揺れが生じ、それが増幅する。ただし、ブランコではバネ付き振り子と異なり、人がブランコの上で屈伸運動することによって、重心の上下運動にエネルギーを供給することができるが、人が屈伸運動を止めても、摩擦によるエネルギーの散逸がなければ、ブランコは振り子となって減衰することなく振れ続けることができる。
参考:ブランコとボタフメイロ

コメント