円の面積から球の体積へ、さらに高次元球へ

　半径 $a$ の円の円周の長さは2 $\pi a$ 、これは円周率の定義でもあるが、円を円の中心を頂点とする二等辺三角形に分割して考えれば、円の面積は、積分を用いなくても、円周×半径÷２として簡単に求めることができる。しかし、ここでは、微積分を学習する意味から、あえて積分して求めることにしよう。半径 $r$ の円の円周2 $\pi r$ を、半径 $r$ で0から $a$ まで積分することによって求められ、その値は $\pi {a }^{ 2 }$ となる。また、別の方法として円の面積は円の曲線の方程式から求めることもできる。半径 $a$ の円の方程式は、

　　　 ${ x }^{ 2 }+{ y }^{ 2 }={ a }^{ 2 }$ 　　　　　(1)

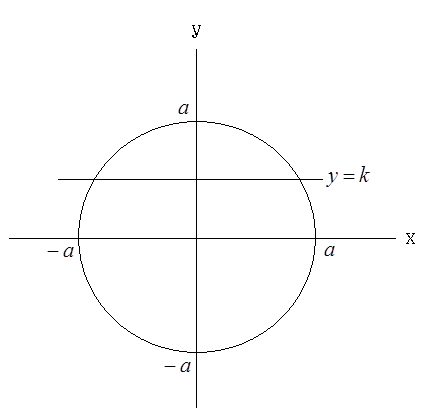
と表わすことができる。ここで、- $a$ < $k$ < $a$ として、 $x$ 軸に平行な直線 $y=k$ が曲線(1)によって切り取られる長さ、2 $\sqrt { { a }^{ 2 }-{ k }^{ 2 } }$ を $k$ で $-a$ から $a$ まで積分しても円の面積を求めることができる。この積分は少々難しいが、 $k$ = $a$ sinθと変数変換すればできよう。

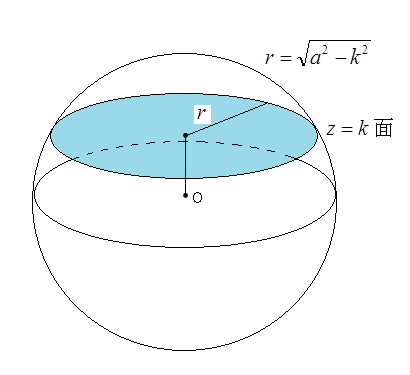
　円の面積を求める上記の方法を三次元に拡張すると、球の体積を求めることができる。原点0を中心とする半径 $a$ の球の球面の方程式は、

　　　 ${ x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }={ a }^{ 2 }$ 　　　　　(2)

と表される。この球をz軸に垂直な平面、 $z$ = $k$ 　(- $a$ < $k$ < $a$ )で切ったときの断面は、半径が $\sqrt { { a }^{ 2 }-{ k }^{ 2 } }$ の円となり、その円の面積は、 $\pi \left( { a }^{ 2 }-{ k }^{ 2 } \right)$ となる。それを $k$ で- $a$ から $a$ まで積分すると、球の体積は $\frac { 4 }{ 3 } \pi { a }^{ 3 }$ となる。

　これは球を薄い円盤に輪切りにしたあと、各円板の体積を求め、それを加えて球の体積を求めたことになるが、球を薄い球殻に分けて、球殻の体積を加え合わせても球の体積を求めることができる。つまり、半径 $r$ の球の表面積は球の体積を半径で微分することによって求めることができる。半径 $r$ の球の体積は $\frac { 4 }{ 3 } \pi {r}^{ 3 }$ であるから、表面積は $4\pi{ r }^{ 2 }$ となる。

　ここで、円を二次元の球と考えると、円の面積は二次元球の体積と考えることができる。二次元球の体積から、三次元球球の体積を求めたように、図２を四次元に拡張すると、三次元球の体積から、四次元球の体積を類推して求めることができる。

　4次元球の体積を求める場合、図２における断面円の面積は、半径が $\sqrt { { a }^{ 2 }-{ k }^{ 2 } }$ の三次元球の体積に相当する。その体積を変数 $k$ で、- $a$ から $a$ まで積分すると、4次元球の体積が求まる。結果は ${\pi}^{2}{a}^{4}$ /2となる。これを $a$ で微分すれば、4次元球の表面積が求まる。同様に、五次元球の体積と表面積、一般にはn次元球の体積と表面積を求めることができる。

　これとは別に、ガウス積分を用いる方法がある。今度は先に高次元球の表面積を求め、それを半径で積分して体積を求める。それも微積分の学習にとって、格好の教材であるので、大学生だけでなく、理系大学を目指す高校生にも、併せてその計算方法の習得も是非お勧めしたい。

大学の微積分：高次元球の体積と表面積

コメント