小学生が解く大学院入試問題

2020.10.27 
三辺の長さの和が一定の二等辺三角形のうち、
面積が最大になるものを求め、その理由を示せ

　これは、十数年前、Ｔ大学の大学院理学系研究科の入学試験に出題された数学の問題だが、与えられた条件を満たす二等辺三角形の面積を、１変数の関数として書き表すことができれば、それを微分することによって解ける。それでは、微分を知らない小学生や中学生には、この問題を解く術はないのだろうか。この問題の解法を様々な角度から考えてみよう。

1. 普通の解法

　微分を使わずに解くまえに、まずは微分を使った普通の方法で解いてみよう。

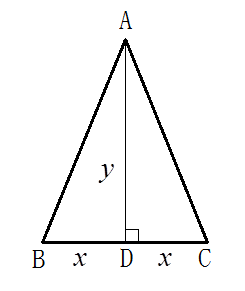
　二等辺三角形ＡＢＣの三辺の長さの和をL 、面積をS、底辺のながさを2x高さをyとすれば、

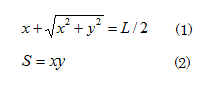
が成り立つ。Lが一定の条件のもとで、Sが最大になるための、xの条件を求めればよい。(1)と(2)からyを消去すると、

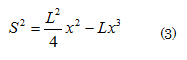
となり、あとは簡単である。(3)式の右辺は、x=0とx=L/4で0となるので、平均値の定理とやらで、0＜x＜L/4の間に極値が存在する。(3)式の微分が0を満たすxの値は、x=L/6、つまり、底辺の長さ2xがLの三分一に等しいとき面積が最大となる。式で書けば次の通りである。

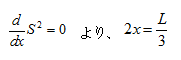
　Ｔ大の大学院で出題された問題では二等辺三角形に限定され、その分、問題が易しくなっているが、三角形一般に広げても面積が最大になるのは正三角形の場合であることに変わりはない。それを証明するにはどうすればよいだろうか。

2.　よりエレガントな解法

　一般に、三辺の長さが、a、b、cの三角形の面積Sは、s=(a+b+c)/2とすると、

　　　S=\sqrt { s(s-a)(s-b)(s-c) }　　　(4)

と表される。これをヘロンの公式という。これより、

　　　\sqrt [ 3 ]{ { S }^{ 2 }/s } =\sqrt [ 3 ]{ (s-a)(s-b)(s-c) }　　　(5)

となり、さらに幾何平均は平均される要素が全て等しいとき算術平均に等しいが一般にはそれ以下であるので、

　　　\sqrt [ 3 ]{ (s-a)(s-b)(s-c) } \le s/3　　　(6)

となる。等号が成り立つのは、三辺、a、b、cの３辺の長さが等しいときであるから、三辺の長さの和、２sが一定のもとで、三角形の面積が最大になるのは、正三角形の場合であり、その最大値は、(5)および(6)式より、{ s }^{ 2 }/\sqrt { 27 }となる。ヘロンの公式を用いた解法は微分を使わずに済む鮮やかな解法だが、小学生や中学生には無理だろう。　

3.　小中学生にお勧めの解法

　次に、微分を使わず、ヘロンの公式も使わず、数式に頼らず、極めて原始的で簡単な、中学生にも、いや、小学生にも理解できて、さらに三角形一般に対する夢のような解法を紹介しよう。

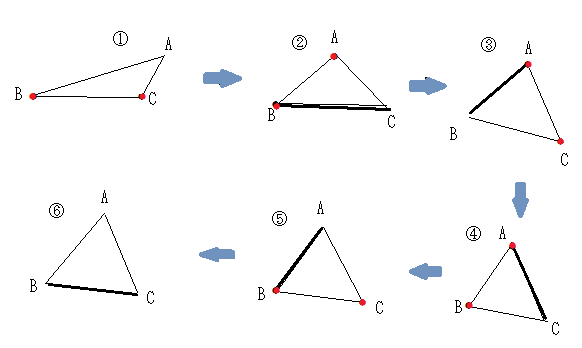
　上図①において、B点とC点をを固定し、三辺の長さの和Ｌを一定に保ちながら点Aを動かすと、A点は、BとCを焦点とする楕円上を動く。このとき、三角形の面積が最大になるのは、底辺BCに対する点Aの高さが最大のときだから、次の三角形②のように、辺ABと辺ACが等しい二等辺三角形である。二等辺三角形②において、今度はAとBとを固定し、C点を移動させたとき面積が最大になるのは、ACとBCが等しい次の二等辺三角形③になる。さらに③において、AとCを固定し、Bを動かすというように、同様な操作を次々と繰り返す。二等辺三角形の面積はだんだん大きくなるとともに、三辺の長さが等しくなっていき、二等辺三角形は正三角形に限りなく近づく。正三角形に対して、この操作を行っても面積は増えない。つまり、三辺の長さの和が一定の三角形でその面積が最大の三角形は正三角形である。二等辺三角形から次の二等辺三角形に移るごとに、面積は増え、長さの異なる二つの辺の長さが平均化されるだけだから、三辺の長さの和Ｌは一定に保たれる。

4.　熱力学的解法

　次に、小中学生には勧められないが、2.と3．の解法に熱力学の第二法則を組み合わせた解法を考えてみよう。ヘロンの公式において、長さに温度を対応させ、s-a={T}_{A}、s-b={T}_{B}、s-c={T}_{C}とすると、s　の定義から、{T}_{A}も {T}_{B} も {T}_{C}も、いずれも正の数であり、その平均はs/3となるが、{T}_{A}、 {T}_{B}、 {T}_{C}を理想気体の温度と考えてみよう。

　ある種の理想気体が等量ずつ、三つの容器、A、B、Cに入っていて、三つの容器で気体の温度は異なり、最初は、それぞれの温度が、{T}_{A}、 {T}_{B}、 {T}_{C}であったとする。ここで、まず、AとBとを熱的に接触させ、十分時間が経過すると、両者とも熱接触させるまえの温度の平均に等しくなる。つまりAとBの気体は熱平衡状態になる。このとき、熱は容器の気体の間で移動するだけで、外部に漏れないとする。また外部から入ってくることもないとする。

　熱平衡になったAとBとを離して熱接触を断ち、次にBとCとを熱接触させて熱平衡になったあと離し、さらにCとA、さらに再びAとB、BとC、・・・というように無限に繰り返していくと、A、B、Cの温度はいずれも、{T}_{A}と {T}_{B}と {T}_{C}の三つの温度の平均温度s/3に等しくなり、それ以上変化しない。

　上記、一連の操作により、容器Aの気体の温度は、始状態では{T}_{A}=s-aであったのが、終状態ではs/3となる。その過程は不可逆過程であるが、その間のエントロピーの変化は始状態と終状態を可逆過程で結ぶことによって計算できる。

　　　\Delta { S }_{ A }={ C }_{ V }\log { \frac { s }{ 3\left( s-a \right) } }

ここで、{ C }_{ V } は一つの容器Aのなかの気体の定積熱容量である。容器B、容器Cのエントロピー変化も同様にして計算できる。容器A,B,Cからなる系のエントロピーの変化量⊿{S}_{total}は、部分系、A、B、Cのエントロピーの変化量の和であるから、

　　　\Delta{ S}_{total}={ C }_{ V }\log { \frac { { s }^{ 3 } }{ 27\left( s-a \right) \left( s-b \right) \left( s-c \right) } }

となる。孤立系のエントロピーの増加は0または正であるから、そのためには、\left( s-a \right) \left( s-b \right) \left( s-c \right) \le { s }^{ 3 }/27でなければならない。ヘロンの公式から三辺の長さが、a、b、cの三角形の面積をSとすると、{ S }^{ 2 }\le \frac { { s }^{ 4 } }{ 27 }となる。よつて、三辺の長さの和が2sである三角形の面積の最小値は \frac { { s }^{ 2 } }{ 3\sqrt { 3 } } となり、当然のことだが、2.の結果と一致する。

５．おわりに

　冒頭の問題に対して４つの解法を紹介したが、大学院受験者には、前者の１．と２．の解法を勧める。後者の３．や４．は、出題者や採点者によっては、正解とは見做されない危険性があるからである。それでも、ここで敢えて、後者二つの解法を紹介したのは、実際の研究においては、奇抜な着想のなかに、問題解決の意外な糸口が隠されている場合が多いからである。

　　　難しいことを易しく
　　　易しいことを深く
　　　深いことを面白く
　　　　　―　井上ひさし　―

コメント

タイトルとURLをコピーしました