水中の物体は物体が押しのけた水の重さだけ軽くなる
筆者が、アルキメデスの原理とも呼ばれる浮力の法則を習ったのは中学の理科の時間であった。

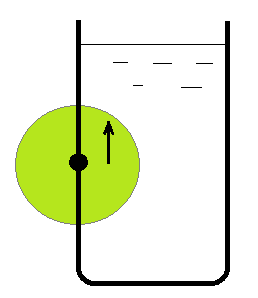
水中の物体に働く水圧は、図1のように、物体の表面に垂直に働き、深い所ほど大きくなるため、物体には周りの水から上向きの力、つまり、浮力を受ける。
浮力は、物体の表面に働く周囲からの水圧の和だから、物体の材質によらない。物体の形状が同じなら、重い物体でも軽い物体でも浮力は同じである。物体を周囲の水と同じ重さのもので置き換えても浮力は変わらない。それなら、いっそ水そのもので置き換えたらどうなるか。
物体の代わりに置き換えられた水は水の中で静止している。それなら置き換えられた水に働く浮力とその水に働く重力とは釣り合わなければならない。つまり、押しのけた水の重さだけ軽くなるというアルキメデスの原理が成り立つ。
中学の理科の先生はバネばかりと台秤を使って、実験をしながらして説明してくれたので、よく理解できた。さらに先生は、例の王冠の話をしてくれた。このとき、少年は 将来進むべき道を見つけた。
芸能界、スポーツ界、政治の世界はどれも無理。文筆家、芸術家、音楽家はもっと無理。 Eureka! そうだ、アルキメデスになろう、これしかないと。
大学の物理学科に入学後、再度アルキメデスの原理に出会ったのは教養部のときの物理学の授業であった。海に浮かぶ氷山や船のように、全部が水に浸かっていない場合にも浮力の原理は成り立つ。それなら、次の図2のように半分だけ水に浸かった円盤でも、水に浸かっている右半分だけに浮力が働き円盤は回転するだろうか。
円盤が回転するなら永久機関が作れることになるが、もちろん回転はしない。水槽と円盤の隙間から水が漏れず、両者の間の摩擦の小さい装置を作るのは難しいが、これは技術的なことを問題にしているのではない。装置を作ることができたとしても、この装置は原理的に回転しない。
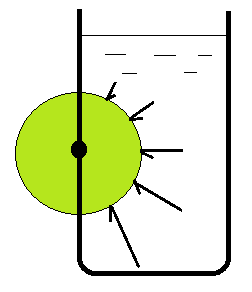
浮力の法則が導かれる過程を学ばず、その結果だけを鵜呑みにしていると、円盤は左まわりにまわるかのように錯覚するが、水に浸かっている円盤の右半分に働く浮力は垂直上向きではない。次の図3のように水圧は物体の表面に垂直に働くので、すべて回転中心に向かい、トルクをつくらないから回転しない。
その後、アルキメデスの定理に三たび関わることになったのは、教職に就き、今度は学生にベクトル解析を教えていたときである。
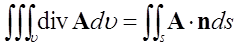
ガウスの定理の証明は他に譲るとして、領域内のベクトルの「発散」の総和は、領域を囲む閉曲面を内から外に貫くベクトル量の総和に等しいというガウスの定理は、3重積分が2重積分に、あるいは逆に2重積分が3重積分で表されることを示している。

上記のような高校で学ぶ定積分も、直線上の関数の「傾斜」の総和が、積分領域の二つの端点での関数の値で決まることを意味している。両者の類似を考えれば、ガウスの定理を理解するのは、さほど難しいことではなかろう。
ちなみに、ストークスの定理は、閉曲線を縁とする曲面上のベクトルの「回転」の総量が、閉曲線上の線積分に等しいことを意味する。「発散」も「回転」も「傾斜」も微分演算子である点ではどれも同じである。
ガウスの定理もストークスの定理も、電磁気学にとって極めて重要な定理であるが、ガウスの定理を、アルキメデスの原理の証明に使えないだろうか。
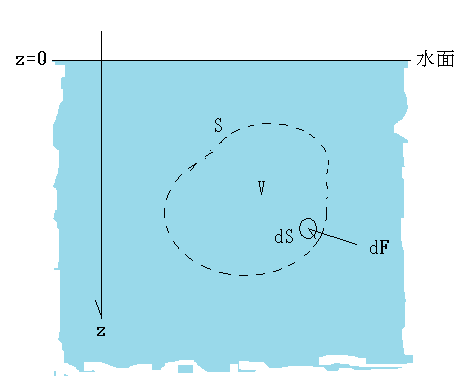
図4のように、座標軸のxy面を水面に選び、z軸を鉛直下向きに選ぶ。zは水深になる。x、y、z軸方向の単位ベクトルをそれぞれ、i ,j ,k とする。水中に閉曲面Sで囲まれた領域Vを考え、閉曲面上の微小面積dSに働く力をdFとし、曲面に垂直で外向きの単位ベクトルをnとし、水の密度をρ、重力加速度の大きさを とすると、
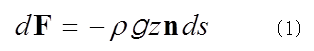
(1)式の総和が浮力Fとなる。

浮力Fの成分、Fx、Fy、Fz は、(2)式と、 i ,j ,k それぞれとのスカラー積をとることによって得られる。例えば、Fx は、

(3)式の右辺の面積積分にガウスの定理を用いて体積積分に変えると、
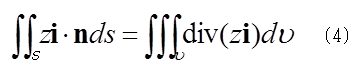
となるが、(4)式の右辺の被積分関数div(zi) は0であるから、Fxは0である。同様に、div(zj)も0であるからFyも0である。しかし、div(zk)=1であり、Fz=-ρv 、よって、F= -ρv
k となり、アルキメデスの定理が証明できる。
しかしながら少年の日の夢は破れ、一度も大通りを絶叫して走ることなく、定年退職となって早や10年、今、次世代科学者を目指す少年少女に、あの日の夢を託したい。

コメント