渇水期の皿洗い
給水車から貰ってきたバケツいっぱいの貴重な水で数枚の皿を洗うにはどうすればよいだろうか。全ての皿を一度にバケツの水に漬けて洗うのは賢明な方法ではない。水を三つぐらいの容器にわけ、皿を一枚ずつ、まず、容器Aの水で洗い、その皿をつぎに容器Bの水、最後に容器Cの水で洗って仕上げる。容器Aの水はすぐに汚くなり、容器Bの水もある程度は汚れるが、それほどでもなく、容器Cの水はかなりきれいなままであろう。
分割数を増やすほどよいが、水を複数の容器に分割することにより、少ない水である程度全ての皿がきれいに洗える。汚れている皿を始めからきれいな水で洗う必要はない。最初は汚れた水で洗い、ある程度きれいになった皿はある程度きれいな水で洗うのである。
麦茶の冷却
渇水時の皿洗いの手法を熱力学に応用できないだろうか。今、沸かしたての熱い麦茶を、それと等量の冷たい水で冷やすことを考えてみよう。熱は麦茶と水の間だけで交換され、それ以外に、外部への熱の流出も、外部からの熱の流入もないという条件のもとで、麦茶の温度をどこまで冷やせるだろうか。
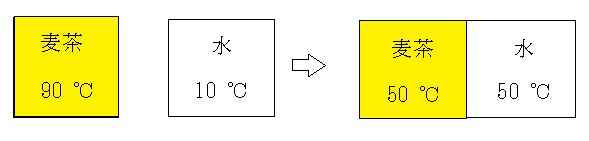
まず、90℃の沸かしたての麦茶とそれと等量の10℃の水があるとし、両者の比熱は等しいとしよう。両者を熱的に接触させると、麦茶から水に熱が移動し、麦茶の温度は下がり、水の温度は上がり、両者の温度差は狭まる。温度差がなくなり、両者の温度がともに50℃になると熱の移動はなくなり、麦茶と水は熱平衡状態となり、それ以上、麦茶も水の温度も変化しない。
可逆的熱交換
それでは、麦茶を50℃以下に冷やす方法はないだろうか。渇水時の皿洗いの方法を思い出してみよう。まず、麦茶と冷水をそれぞれ二つの容器に二等分しよう。麦茶を容器AおよびBに分割し、水を容器αおよびβに分割する。分割しただけだから、この段階でAとBの温度はともに、90℃、αとβは10℃のままである。これを下の図のように次々に熱的に接触させていこう。
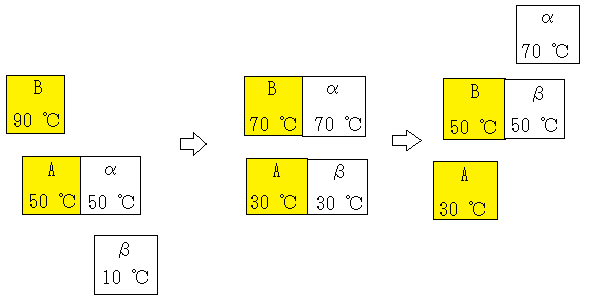
まず、第一の操作でAの麦茶とαの水を熱的に接触させると、熱平衡になったあとは、両者の温度はともに50℃となる(上図の左の状態)。次に第二の操作では組み合わせをずらして、50℃になった麦茶Aと10℃のままの水β、および、90℃の麦茶Bと50℃のαを熱接触させる。その結果は、Aが30℃、Bが70℃、αは70℃、βは30℃となる(上図の中央の状態)。さらに第三の操作で、70℃の麦茶Bと30℃の水βを接触させると、両者は50℃になる。結局、三つの操作を終了した段階(上図の右の状態)では、麦茶Aは30℃、麦茶Bは50℃となる。水のほうは、αが70℃、βが50℃となる。麦茶の平均温度は40℃となり、50℃以下に冷やされている。
次に麦茶と水をそれぞれ3等分して、同様にして次々に熱接触させて冷やせば、三等分した麦茶の温度はそれぞれ50℃、35℃、20℃となる。4等分では、50℃、37.5℃、25℃、15℃の麦茶が得られる。手計算では、5分割あたりが限度だが、エクセルの計算機能を用いて、分割数を増やしていけば、麦茶全体の平均温度は限りなく10℃に近づき、水の温度は90℃に近づく。つまり、分割の数が無限大の極限では、麦茶と水の温度を完全に入れ替えることができる。
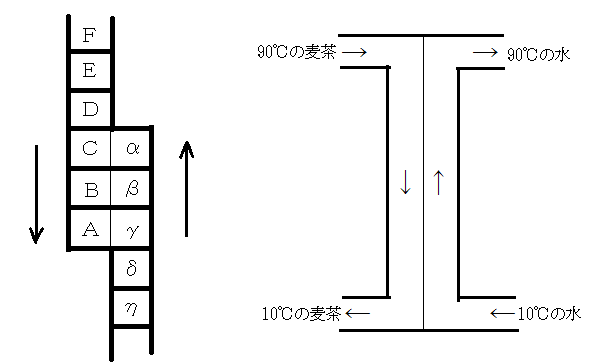
上記の考えを応用したのが熱交換器である。麦茶と水の流れを逆にすれば、麦茶は次々と異なる相手の水と熱交換を行う。しかし、麦茶と水を同方向に流すと、麦茶と水を分割しないで冷やす場合と同じであり、麦茶は50℃までしか冷えない。前者は可逆的熱交換であり、後者は不可逆的熱交換である。可逆的熱交換では、熱い麦茶は熱い水で冷やされ、冷たい麦茶は冷たい水で冷やされる。つまり、冷やされる麦茶と冷やす水との温度差が小さい。それに対し、不可逆的熱交換では、いきなり、熱い麦茶と冷たい水が出会うので、大きな温度差で熱が移動することになる。
食器を拭くのは布巾、テーブルを拭くには台拭き、床を拭くのが雑巾だが、布巾も使ううちに汚れてくるので、そうなれば、格下げして台拭きとして使い、さらにその後雑巾として使えばよい。しかし、新しい布巾をいきなり雑巾として使ってしまうと、そのあと、台拭きや布巾としては使えないことと同じことである。
リービッヒの冷却器
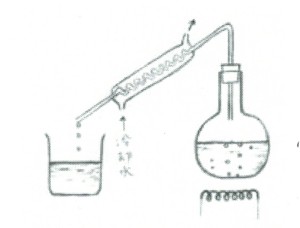
上図は中学の理科実験で蒸留水をつくるのに用いられるリービッヒの冷却器とよばれる熱交換器である。高温の水蒸気を上から下に向かって流し、冷却水は逆に下から上に向かって流す。冷却器の上部から出る水は熱湯になっていて、うっかり触れるものならやけどをするが、水蒸気は充分冷やされて蒸留水となり、ビーカーに落ちる。冷やされるものと冷やすものの流れを逆方向にし、次々と相手を変えて熱交換をすることが重要である。
麦茶の色の入れ替え
麦茶の冷却では、分割数を増やして、次々に相手を変えて熱接触させることによって、麦茶と水の温度が入れ替わったが、熱接触させるだけでなく、麦茶と水を混ぜ合わせたらどうなるだろうか。
分割しないで混ぜれば、温度だけでなく、色も香りも味も平均化される。つまり、希釈されて量が倍になり、温度が50℃の薄い麦茶ができるだけである。しかし、麦茶と水をそれぞれ多数の容器に分割して、麦茶の容器と水の容器とが出会うごとに、混ぜ合わせて次の操作に移れば、温度も色も香りも味も入れ替わる!つまり、無限に分割すれば、90℃の麦茶とそれと同量の10℃の水となり、もとのままである。
次々と混ぜ合わせて、平均操作をしたのに、全ての操作が終わったあと、90℃の麦茶と10℃の水になるだけであり、何も起きていないことと同じである!振り子に譬えれば振り子が揺れて1周期のあと、元の状態に戻るのと同様である。何か騙されたような気になるが、麦茶の冷却に用いた物理法則は、熱は高温から低温に向かって流れ、温度差がなくなれば、熱は流れないという中学の理科で習う知識だけである。また数学の知識としては、二つの数値を足してニで割れば、平均値になるという、数学と言うより算数の知識だけである。
参考文献
世戸憲治「浴槽の物理学」数理科学 No.172, OCTOBER 1977 p.73

コメント
はじめまして あつこさんのブログから来ました。
とても面白かったです。 また来ます。
知らない方からは初めてのコメントです。娘のホームページともども
よろしくお願いします。