1.仕事の定義
岩波書店発行の広辞苑(第四版)には、力がする仕事について次のように記述されている。
「力が働いて物体が移動した時に、物体が移動した向きの力と、
移動した距離との積を、力が物体になした仕事という。」
しかし、同じく岩波書店発行の、理化学辞典(第三版)では、仕事を次のように定義している。
「力学系に力F が作用し作用点がdr だけ変位するとき、
スカラー積F・dr を、その力が力学系になした仕事という。」
どちらも作用した力と動いた距離との積であるが、動いた距離が、広辞苑では物体が動いた距離、つまりの重心が動いた距離であるのに対し、理化学辞典では、力の作用点が動いた距離である。広辞苑および理化学辞典によって定義された仕事を、それぞれ、仕事Aおよび仕事Bと呼ぶことにしよう。物体が質点の場合には、仕事Aは仕事Bに含まれてしまう。しかし、仕事の対象が、変形や回転も可能な、一般の物体であれば、仕事Aは仕事Bとは異なる仕事になる。
高校の物理教科書での仕事は、広辞苑にならって仕事Aであるが、高校の物理でも、質点の運動のみを扱ってはいないので、仕事Aは仕事Bとは異なる仕事だと考えざるをえない。どちらも一般の物体を対象とした仕事である。
仕事A=力×重心の移動距離
仕事B=力×作用点の移動距離
2.抗力と仕事
仕事Aと仕事Bの違いが際立つてくるのは、物体あるいは系に働く外力が抗力を含む場合である。抗力は作用点が動かないので仕事Bには寄与しない。一方、物体の重心が動けば、仕事Bに寄与しない抗力も仕事Aに寄与することになる。
一般に、力学系の運動は、系の並進運動(重心の運動)と重心の周りの相対運動からなるが、そのうち系の並進運動に外力がなす仕事が仕事Aである。かたや仕事Bは系全体に対してする仕事である。
熱力学や材料力学では、系の並進運動を考えることはないので、仕事Bだけで事足りるが、ボールや人や車の運動など、日常扱う物体では、物体の並進運動が第一義的であるから、仕事Bだけでは不十分であり、仕事Aが必要である。仕事Aと仕事Bは、異なる仕事だが、どちらも正しい真の仕事であり、力学にとってどちらも必要な仕事である。
3.抗力のなす正負同時一対の仕事
抗力が仕事をすると言えば、奇異な感じを与えるかも知れないが、抗力が仕事をする場合は、正の仕事と負の仕事を同時に行っているので、エネルギー保存則には反しない。次に、抗力が仕事をする二つの例を紹介しよう。
3-1.内力が存在しない場合
図1のように、半径 、質量
、中心軸のまわりの慣性モーメント
の円柱を考え、円柱に巻きつけた糸を、右方向に引っ張り、円柱を水平な床の上で転がしてみよう。
 糸の張力を
糸の張力を 、円柱が床から右方向に受ける水平抗力(静止摩擦力)を
、円柱の重心
の座標を
、円柱の右回りの回転角をθとする。円柱の重心の並進運動および回転の運動方程式は、それぞれ、
![]()
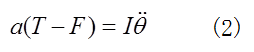
となる。ここで、円柱に働く水平抗力の向きが気になるが、円柱の慣性モーメントは、 であるから、(1)と(2)より、F=T/3 となる。 水平抗力は、張力 と同じく、図1のように、右向きに働くことが分かる。
力の作用点Pを微少距離 だけ右に変位させたとき、重心Gの変位を
、角度θ の変位をdθ とすれば、
、および、
が成り立つ。
(1)の両辺に をかければ、
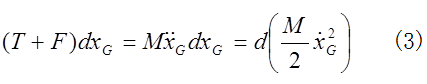 また、(2)の両辺に
また、(2)の両辺に をかければ、
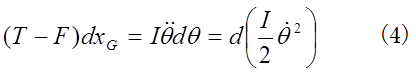 となる。
となる。
(3)式の右辺は円柱の並進運動のエネルギーの増し分であるから、左辺は力(T+F)が円柱の並進運動にした仕事であり、仕事Aの定義に一致する。また、(4)式の右辺は回転運動のエネルギーの増し分であるから、この式の左辺も力(T-F)と重心の移動距離との積であるが、右辺は円柱の回転の運動エネルギーの増分であるから、左辺は力(T-F)が円柱の回転運動にした仕事である。張力Tは並進運動と回転運動の両方にTdxGの仕事をするのに対し、水平抗力Fは重心運動にFdxG の仕事をし、回転運動に-FdxG の仕事をしている。つまり、抗力 は、並進運動と回転運動に、正と負一対の仕事を同時にしている。
円柱に働く外力(T+F) は円柱の並進運動に仕事をし、そのエネルギーを増すとともに、円柱に力積を及ぼし、円柱の並進運動の運動量を増している。つまり、並進運動のエネルギー増分も運動量の増分も、重心の運動方程式(1)式から導かれるので、並進運動に仕事をする力と力積を及ぼす力はどちらも(1)式の左辺の力T+Fである。もし、運動量に寄与する力と並進運動のエネルギーに寄与する力が異なると考えるのは、‘木に竹を接ぐ’ことになろう。
(3)と(4)を加えると、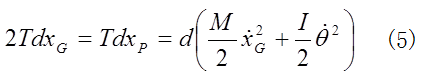
となり、これは仕事Bの定義に一致する。(3)式の仕事には、抗力も含めたすべての外力が寄与するが、円柱全体の運動にする仕事(5)式には、作用点が動かない水平抗力は現れない。
運動方程式(1)と(2)から、先に、まず、F を消去すれば、(3)と(4)式を経由せずに(5)式が直接導かれるが、(5)式だけでは、人の手の筋力がした仕事Tdxpが並進運動と回転運動にどのように配分されるかが分からない。
3-2.系内に動力源が存在する場合
自転車に乗って道路上で加速するとき、乗り手の筋力は駆動輪である後輪の回転運動に仕事をすることができる。後輪の運動に対しては、筋力は外力だからである。しかし、自転車と乗り手からなる系に対して、筋力は内力であるから、系の並進運動に直接には仕事をできない。 図のように、自転車が加速しながら、dxだけ進むとき、後輪に道路から前向きに働く水平抗力をF、前輪に後ろ向きに働く水平抗力をfとしよう。
図のように、自転車が加速しながら、dxだけ進むとき、後輪に道路から前向きに働く水平抗力をF、前輪に後ろ向きに働く水平抗力をfとしよう。
人と自転車を一つの系と考え、後輪と前輪を、どちらも系のなかの部分系と考えよう。力として、人の筋力、抗力F、および抗力fを考え、運動の形態として、系の並進運動、後輪の回転運動、前輪の回転運動を考えるとしよう。
まず、筋力は系に対しては内力であるから、系の並進運動に対しては、直接には、仕事をすることはできない。これは宇宙飛行士が宇宙空間で手足を動かしても外力がなければ前進できないのと同じである。しかし、筋力も部分系の後輪に対しては、外力であるから、ペダルとチェーンを通して仕事をすることができる。また、前輪に対しては仕事をすることはできない。
次に水平抗力Fは、系に対しても、部分系の後輪に対しても外力であるから、系の並進運動に対しても後輪の回転運動に対しても仕事をすることができる。前者にする仕事はFdxであり、後者にする仕事は-Fdxである。抗力Fは正負同時一対の仕事をすることによって、後輪の回転エネルギーの一部(大部分)を並進運動に変換させている。
最後に抗力fは系の並進運動と、前輪の回転運動に仕事をすることができる。前者の仕事は-fdxであり、後者の仕事はfdxである。抗力fも正負同時一対の仕事によって、並進運動に一部を前輪の回転運動に変換している。
上記のことを表にすると次のようになろう。 自転車の後輪を道路から浮き上がらせた状態で、ペダルを踏んでも、後輪を回転させることはできても、自転車を加速させることはできない。抗力が働かなければ、抗力のなす同時一対の仕事ができないからである。
自転車の後輪を道路から浮き上がらせた状態で、ペダルを踏んでも、後輪を回転させることはできても、自転車を加速させることはできない。抗力が働かなければ、抗力のなす同時一対の仕事ができないからである。
「抗力なす正負同時一対の仕事」がその威力を発揮するのはブランコの原理を説明する場合であろう。それについては当ホームページのブランコとボタフメイロを参照して頂きたい。
4.「偽の仕事」批判
力と作用点の移動距離の積が真の仕事(real work)であり、力と重心の移動距離の積は偽の仕事(pseudo work)とする論文1)があるが、その考えを、円柱の運動の例に適用すれば、(5)式の左辺のみが真の仕事であり、(3)式や(4)式の左辺は、偽の仕事ということになる。しかし、(3)と(4)の両式とも、右辺は真のエネルギーの、真の増し分である。また、(3)と(4)の左辺の「偽の仕事」どうしを加えると、(5)式の左辺の真の仕事になるというのも説明に窮しよう。
Pseudoworkは30年ほど前にアメリカで提唱された考えで、それ以前には、偽の仕事などはなかった。それでも、それまでの力学教育に不都合を来たすことはなかった。そして、それ以後の力学教育においてもpseudoworkが登場することは、ほとんどなかった。Pseudowork 以前から、既に、仕事Aが、物体の並進運動に対する真の仕事として定義されていたからである。
古典力学は既に完成した学問であり、仕事というその根幹に関わる部分に得体の知れないpseudoworkなどが迷い込む隙間はない。古典力学にとって、ニュートンの運動方程式が最優先であり、アメリカファーストではない。仕事の定義もニュートンの運動法則に則っていなければならない。「系の並進運動になす仕事」も「抗力のなす正負同時一対の仕事」も運動方程式から極めて自然に導かれる仕事である。
5.おわりに
芥川龍之介の「蜘蛛の糸」のパロデイを創るなかで、ふと思いついた仕事についての疑問、罪人のカンダタが蜘蛛の糸を登るとき、重力場のなかのカンダタに仕事をしたのはカンダタの筋力か、それとも蜘蛛の糸の張力か?この問題提起2)に端を発し、その後も、日本物理学会や物理教育のメーリングリストなど張力説を主張した結果、筋力説を主張する人々との間で激しい論争となり、「大学の物理教育」には、二度にわたり投稿するも「教育実践ではない、議論しても意味がない」という、理由で掲載を拒否された。
編集委員会も教育研究で多忙な中でのボランテイア活動であり、あまり粘るは気の毒である。まだ、まだ、‘地ならし’が足りないようだから、ここは、一旦ひいて、既に退職の身、京都見物がてらに、もう一度、次の学会で発表し、広く物理学会々員のご意見を求めることにした(2018年秋、日本物理学会物理教育分科会で発表の予定)。
筋力説も張力説も、エネルギーの出所は筋力であり、張力や抗力は、そのエネルギーを貰って仕事をするのだから、日常会話なら、筋力説でもよいだろう。しかし、力学では、カンダタの重心運動に仕事をするのは蜘蛛の糸の張力、自転車なら道路からの抗力だと考えなければ整合性がとれない。日常用語と物理用語が一致しないのは珍しいことではない。
仕事Aは、本来、物体の並進運動になす仕事として定義されていたのであるから、現行の辞典や教科書の仕事の定義を見直す必要はない。Pseudowork が登場する以前の、昔の解釈に戻るだけであり、物理教育に混乱が起こる恐れも一切ない。
今回、最初は、四面楚歌の圧倒的に不利な状況のもとでの論争となり、(疑惑その1:冤罪説)のなかの、お釈迦様の逆鱗に触れ、見捨てられたたカンダタや、蜘蛛の糸に絡まり八方ふさがりとなったカンダタ(疑惑その2:捏造説)の苦しみも体験したが、今では、抗力派も増え、幸運にも地獄からの脱出に成功した(疑惑その3:悪人正機説)気分である。
三つのパロディのなかの三者三様のカンダタを、二年余りに亘る論争の中で体験し、楽しむことができたが、相手だけでなく、返されると、仕掛けたほうも大変な痛みを伴うというプロレス技の「足4の字固め」のように、双方ともが、多大な心身の疲労を強いられた今回の論争に、労力を厭わず参加して頂いた方々に、筋力派、張力派(抗力派)を問わず深く感謝したい。
参考文献
1)Bruce Arne Sherwood: Pseudowork and real work, , Am.J. Phys.,Vol.51, 1983
2)後藤信行:「蜘蛛の糸」仕事をしたのはカンダタの筋力か? 日本物理学会誌 Vol. 71, No. 2, (2016)
二つの仕事
 力学
力学
コメント