うさぎが餅をつき、かぐや姫の住むという月。だが、アポロ宇宙飛行士が見た月は、水も空気もなく、ただ荒涼とした世界であった。しかし、科学は、地球に最も近い天体に古代から寄せられてきた人々の夢とロマンを壊しているだけではない。人間の知的好奇心と創造力は、科学的観測によって、天空を舞台とする胸躍る新たな物語を創り出している。
飛鳥の才女に恋して
熟田津に船乗りせむと 月待てば
潮もかなひぬ 今は漕ぎ出でな
恋人の許へ船出する夜の、馳せる思いを詠んだ恋歌であろうか。それとも未知の大海へ向かう若者の力強い旅立ちの歌だろうか。史実によれば、斉明天皇が新羅出兵のため、九州の娜の大津へと航海した661年、途中、現在の松山市の熟田津に立ち寄ったとき、一行が再び出航する際に、時の閨秀(けいしゅう)歌人、額田王(ぬかだのおおきみ)が天皇にかわって詠んだ歌という。
伊豫の海を照らす万葉の月も、今宵、稲佐山の空高く、メルヘンの世界へと誘う月も、月は天地創造の時以来、我々に絶えず同じ面を向けながら、一定の軌道上を巡り続けてきたのだろうか。そして、これからも未来永劫にわたって同じ運動をくりかえすのだろうか。
万物は流転する 。宇宙という、ほぼ完全な真空中を、何物とも触れ合うことなく運動する月は、摩擦とは一切無縁のように思える。しかし、潮汐による海水と海底との摩擦は地球の自転を遅らせるのみならず、地球から遥か38万㎞の彼方を運動する月に影響を及ぼし、僅かずつながら、その軌道を変えているのである。
月を愛で、花を眺めて歌を詠む、万葉歌人の風雅とともに、森羅万象の背後に潜む美しい自然の摂理に触れたとき、新たな感動と癒しがある。
ふるさとは遠きにありて
貧しい身なりの旅の僧が筑後川の渡しにさしかかり、渡し賃を持たず途方にくれていると、親切な渡しの船頭はただで向こう岸まで乗せてくれ、僧がそのお礼にと、筑後川の岸辺に生い茂る葦の葉を取って川に投げ込むと、葦の葉は魚になって筑後川を泳ぎ始めたという。
筑後川のほとりの町、城島に古くから伝わる伝説である。僧は弘法大師というとても偉いお坊さまであり、現在、筑後川に生息しているエツという珍味の魚は、そのとき、弘法大使が投げ込んだ葦の葉だという。
筑後平野を横切り、有明海に注ぐ筑後川。その流域に位置し、背振山系を遥かに望む、酒と瓦の町、これが筆者の生れたふるさと、城島町である。現在では市町村合併により、久留米市の一部となったが、昔、城島町の上流は久留米絣で知られる久留米市、下流は家具の街、大川市であった。
しかし、子供の頃は、どちらが上流か下流かをよく間違えていたものである。筑後川が流れ込む有明海は、潮の干満の差が日本で一番大きく、6~7m程にも達し、さらに筑後平野が平坦なため、満潮のときは城島の少し上流まで潮が溯るからである。
筑後川の流域では、住民の生活は昔から川の潮汐と深い関わりをもっていた。伝説の魚、エツはカタクチイワシの一種で、筑後川以外では、同じく有明海に注ぐ矢部川と中国の揚子江だけに生息するという珍しい魚である。さらに筑後川でもエツの生息している領域は城島より下流に限られている。これは筑後川の潮汐と関係しているらしく、潮目の辺りがエツの棲むのに適しているそうである。
筑後川の堤防の内側の河川敷は、現在では、ゴルフ場などになっているが、戦後間もない頃までは、筑後川やその支流の川岸には多くの瓦工場が立ち並んでいた。車が今ほど普及していなかった当時、製品の瓦や、その原料である土や、燃料の石炭などを荷車で運ぶのは大変な労力であった。しかし、川の流れを利用し、船で運べば楽である。潮の流れに乗って、船は少ない燃料で上流と下流の間を往復できるからである。
筑後川の潮の干満は城島の農業にも深く関わっていた。筑後川の支流からクリークに農業用水を引き込むのにも当時は川の潮汐を利用していたからである。川が満潮になる頃、水門を開いて、水をクリークに流し込み、潮が退き始める前に閉じるのである。まさにその潮時を逃さないように、農家では、月齢や、満潮の時刻をいつも気にかけていなければならなかったのである。
潮の干満から時刻を知っていた名残として、英語にもTime and tide wait for no man という諺がある。tideとは潮汐のことであり、timeはこのtideを語源としている。因みに、この諺の日本語訳として用いられる「歳月人を待たず」は晋時代の詩人、陶淵明の詩の一節である。
河川を潮汐が溯る現象としては銭塘江の海嘯やアマゾンのポロロッカが有名であるが、川の水に働く月の引力は地球の重力に逆らって直接川の水を上流に引き上げるほど強力ではない。川を水が溯るのは、川が流れ込む湾内に起きる潮汐によって河口の水位が高くなるためである。さらに湾内の潮汐は一種の共振現象であり、一般に湾内の潮汐は海洋の潮汐よりずっと大きくなる。カナダのファンディー湾での干満の差は世界最大で16メートルにも達するという。
水がいっぱい入った洗面器を水がこぼれないように持って歩くのは容易でない。洗面器が少し揺れると、中の水は大きく揺れるからである。洗面器の水と同様に、湖や湾内にも、その形状に依存した固有振動が存在している。この固有振動はフランス語でseicheと呼ばれているが、日本では静振と訳されている。
湾のなかの静振が湾の入り口での海洋の潮汐によって揺さぶられ、共振すると、有明海やファンディー湾のような大きな干満の差が生じることになる。湾内の潮汐は、海洋の潮汐によって引き起こされる共振現象であるので、埋め立てなどで湾の形が変わると、共振条件が変わるので、湾内の潮汐に影響を与えることがある。
海洋、湾、河川と、潮汐のしくみは少しずつ異なるが、直接的であれ間接的であれ、いずれの潮汐も、もとを辿れば月の引力に起因していることに変わりはない。月が昇り浜辺に潮が満ちてくるのを見て、また川を潮が遡るのを見て、古人は何を考えただろうか。
潮汐が月に関係していることは古代から知られていたにもかかわらず、潮汐と月を結びつけた民話や伝説は見当たらない。その日の生活に追われ、月と潮汐の因果関係などについて考える余裕などなかったのだろうか。それとも、海岸や川の流域の住民にとって潮汐があまりにも日常的なことで、別段、不思議なこととは考えられなかったのだろうか。
月と潮汐の間の因果関係が明確になったのは、ニュートンの万有引力の法則発見以後である。ニュートンは、りんごが木から落ちるのを見て、万有引力の法則を発見したと伝えられている。ニュートンとりんごの逸話は、その真偽はともかく、当たり前のことを当たり前とせず、こだわりを持ち続けることの大切さを我々に教えている。
「ニュートンは、筑後川の水が溯る満月の夜、エツ漁の船の上で、万有引力の法則を発見した。」?! もし、ニュートンが、我がふるさと城島に生れていたなら、そんな話がまことしやかに語り継がれていたに違いない。川は異なるが室生犀星の詩とともに故郷が想い浮かぶ。
うつくしき川は流れたり
そのほとりに我は住みぬ
春は春、なつはなつの
花つける堤に座りて
こまやけき本のなさけと愛とを知りぬ
いまもその川ながれ 美しき微風とともに 蒼き波たたへたり
潮の満引き
随分昔の話だが、昭和三十年代に、胸毛と濃い眉で人気を博した朝潮太郎という奄美徳之島出身の横綱がいた。「日本誕生」という映画にも出演し、原節子の天照大神が隠れた天の岩戸を引き開ける役をやったこともある彼は、もろい一面もあったが、強い時には、打ち寄せる南海の潮汐を彷彿させるような強烈なハズ押しで、相手を一気に土俵の外に押し出したものである。
彼は関脇に昇進すると、四股名をそれまでの朝潮から朝汐に変えたが、当時、筆者はそのことが妙に気になっていた。新弟子の取り組みは早朝だが、幕内の、それも三役、横綱ともなれば、夕方の取り組みになるから、潮を汐に変えたのだろうか。それなら朝汐という四股名は矛盾している、夕汐にすべきではないだろうか。そんなことを考えながら、学校帰りの電気店の店頭に並んだ白黒テレビで栃錦や初代若乃花らとの熱戦を観戦したものである。
潮と汐で潮汐だが、文字通り 潮汐(ちょうせき)は、通常一日に二回起こる。それは月が地球の海に及ぼす起潮力(潮汐力)によって、図1のように、月側の海と反対側の海とが満潮になるからである。月に面した側が満潮になるのは当然のように思えるが、反対側も満潮になるのは何故だろうか。

月は地球の周りを公転しているが、実際には、月と地球を一つの系と考えると、月だけでなく、地球の中心Oも系全体の重心Gの周りを同じ角速度で公転している。つまり、地球も月と一緒にGの周りを公転している。地球と月の質量が等しければ、系の重心は二つの天体を結ぶ線分の真ん中になるが、地球は月の約八十一倍の質量を持ち、地球と月の間の距離は地球半径の約60倍の長さであるので、系の重心Gは、図1のように、地球の中心から地球半径の3/4程度のところにある 。
月に面した側の海水は月に近いので月の引力によって盛り上がり、反対側の海水は、公転の中心Gから遠いので、公転の遠心力によって盛り上がる。尚、図1の海水の膨らみは分かり易いように誇張して描いている。
潮汐についてもう少し数学的な説明を付け加えておこう。しかし、面倒であれば、ベクトルを用いたこの部分は読み飛ばしていただいても構わない。

地球の自転の効果は後で考えることにして、まず、地球は自転していないとしよう。図2において、系の重心Gを起点とし、地球のの任意の点Pに引いた位置ベクトルをr、 Gから地球の中心Oに引いた位置ベクトルをr、さらに、Oから見たPの位置ベクトルをr
とすると、ベクトルの足し算から、r=r
+ r
となる。
Gのまわりに系が公転する角速度をωとすると、点Pに存在する質量mの物体に働く力は、①公転の遠心力=r、②月の引力、これをF
とする。そして③地球の重力=-
r
である。このうち、③は起潮力に寄与しない。①は、
r=
r
+
r
となるが、右辺第一項は、P点の質量を地球の重心Oに置いたときの月の引力と釣り合っているので、-F
に等しくなり、右辺第二項は起潮力に寄与しない。以上からp点における起潮力はF
-F
となる。それは、Pが地球の中心Oに一致したとき0である。つまり、起潮力(潮汐力)は、地球の各部に働く月の引力の、地球中心における引力からのずれによって起こる。
いずれにしても、図1のように海水に働く起潮力によって、月に面した海では月に引き寄せられ、反対側の海では月から遠ざけられる。地球の月に面した側と反対側が満潮になるが、地球は自転しているので、一日に約2回満潮が起こる。
地球の海には、月だけでなく、太陽からの起潮力も働く。天体が地球のある場所に及ぼす起潮力とは、天体の引力そのものでなく、その場所と地球中心とにおける天体の引力の差であるから、天体の引力を距離で微分した量に比例する。つまり、引力は天体までの距離の2乗に反比例するので、起潮力は、天体からの距離の3乗に反比例する。月と太陽と比べると、海水に働く太陽の引力は月の引力の180倍もあるが、太陽までの距離は月までの距離の390倍あるので、太陽の起潮力は月の半分以下となる。
月も太陽も、その起潮力は地球を前後に引き伸ばすように働くので、地球に対して、月と太陽が反対方向に位置する満月のときや、同方向に位置する新月の時は、両者の起潮力が強め合い大潮となる。一方、地球から見て太陽と月の方向が直角のとき、つまり半月のときは、月の起潮力が太陽の起潮力によって、弱められるので小潮となる。また、起潮力は海水だけでなく、地球の固体部分を変形させるように働く。そのため、新月や満月近くになると地震の起こる頻度が増す。
起潮力が一番強め合うのは、地球と月と太陽が一直線上に並んだときであるが、地球の公転軌道面に対して、地球の赤道面は23.5度傾き、月の軌道面は5.2度傾いているので、同じ大潮でも、潮の干満の差はその時々によって少々異なることになる。銭塘江やアマゾンの大逆流現象は、一年のなかで、特定の大潮のときに最も大きくなる。
七里ヶ浜の磯伝い
稲村ケ崎名将の
剣投うぜし古戦場
文部省唱歌にもなった「鎌倉」だが、新田義貞は鎌倉攻めの途中、海岸の道路が海水に遮られて通れなくなっていたとき、海中に一振りの黄金の剣を沈めると、潮が引いて干潟が現れ、鎌倉に攻め込むことができたという。義貞は事前に鎌倉に攻め込むルートの周辺の地形や、潮汐を調べさせ、それを利用して将兵の士気の高揚を図ったものと思われるが、そうだとすれば、まさに名将であろう。
聖書にも同様な現象についての記述があるが、韓国にも海割れという現象がある。韓国の海割れは、5月の大潮とその前後の日の干潮時に、珍島と、それから3キロメートル程離れた島とが陸続きになる現象であり、歌謡曲の「珍島物語」にも歌われている。また、干満の差は場所によっても大きく異なる。日本近海でも太平洋側は1メートルほどあるが、日本海側は十センチメートル程度でしかない。
潮汐摩擦
定量的な議論の場合には、太陽からの起潮力も無視できないが、地球や月の運動への潮汐摩擦の影響を定性的に考える場合には太陽からの起潮力は無視してもよいだろう。ひとまず、地球と月の間の相互作用のみを考えて、潮汐摩擦による運動の永年変化ついて、考えてみることにしよう。
地球の海は月に面している海とその反対側の海が満潮になるが、地球の自転は月の公転より角速度が大きいので、海底は海水より速く運動する。そのため盛り上がった海水は地球の自転に引きずられ、図3のように満潮の位置が自転方向にずれる。
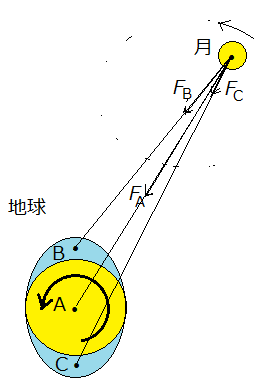
一方、地球の海底は海水を引きずることになるため、地球の自転にブレーキがかかることになる。地球の自転は僅かではあるがだんだんと遅くなる。即ち、一日の長さが伸びることになる。
潮汐摩擦は地球の自転を遅らせるとともに、月にもその反作用を及ぼす。上図のように地球を三つの部分A、B、Cの部分に分けて考えてみよう。
固体部分Aは月に地球の中心方向の力を及ぼすが、海水Bが及ぼす力は中心力からずれ、月の進行方向の成分を持つ。また海水Cは月の進行方向と逆向きの成分を持つ。BとCを比べるとBが地球の直径の分だけ、月に近いのでBの力がCより強い。
地球は月に中心力だけでなく、僅かに月の公転方向にも力を及ぼしていることになるが、公転方向のその成分が月の公転運動に仕事をするため、公転の運動エネルギーが増し、月は遠ざかるのである。
次に、月が遠ざかる理由を角運動量の立場から考えてみよう。地球の海水Bが月に及ぼす力FBは月の公転の角運動量を増やす向きの力のモーメントを作るが、月が海水Bに及ぼす力、つまりFBの反作用力、-FBは地球自転の角運動量を減らす向きに力のモーメントをつくる。二つの力のモーメントの大きさは等しいので、月と地球の系全体の角運動量は一定のままである。
同様なことはFCとその反作用力-FCの関係においても成り立つので、太陽などの他の星から受ける外力を無視すれば、潮汐摩擦が働いても系の角運動量は一定に保たれる。潮汐摩擦によって、地球の自転にブレーキがかかると、地球の角運動量が減少した分、月の公転の角運動量は増加しなければならないのである。
月の速度
潮汐摩擦によって公転方向に力を受けている月の速度は速くなっているだろうか。意外に思えるかも知れないが公転速度は遅くなっていることを注意しておこう。月の公転運動に、エネルギーが徐々に、εだけ補給されたとすると、月の運動エネルギーと位置エネルギーの和がεだけ増加する。
しかし、このときの内訳を見れば、前者はεだけ減少し、後者は2εだけ増加し、全体としてεだけ増加するのである。つまり、エネルギーが増加すると、月は遠ざかり、速度も角速度も減少する。
公転速度について、天体の運動方程式から見てみよう。万有引力の場のなかでの円軌道の場合、公転半径の3乗は公転周期の2乗に比例することが導かれる。これはケプラーの第三法則でもあるが、それから公転速度の2乗は半径に反比例することがわかる。これからも公転運動にエネルギーが徐々に供給され、公転半径が長くなれば速さは減少することが理解できよう。
潮汐摩擦によってエネルギーをもらう月とは逆に、地球を回る人工衛星は、地球の上層大気との摩擦により、僅かに後ろ向きの摩擦力を受け、そのままでは徐々にエネルギーを失い、公転半径は短くなり、公転速度は速くなる。
アポロ計画
アメリカの三十五代大統領、ケネディは、1961年に行った演説のなかで、I believe that this nation should commit itself to achieving the goal, before this decade is out, of landing a man on the moon and returning him safely to the earth.と宣言したが、そのとおりに60年代の最後の年、アポロ十一号のアームストロング船長が人類として初めて月面に立ったのである。
その様子は世界にテレビ中継されたが、月面に立った船長の第一声That’s one small step for man, one giant leap for mankind.という言葉がまだ耳に残る。しかし、アポロ計画において、地球からの距離を測るための反射鏡が月面に置かれてきたことはあまり知られていない。
地球から月までの距離は38万km、往復で76万km、光の速さは秒速30万kmであるから、光は2秒半程度で地球から月までを往復することになる。アメリカはアポロ以後、月面に置いた鏡にレーザー光を当て、光の往復時間を、アポロ以後20年の長期にわたって精密に測り続けた。その結果、月は一年間に3.8㎝ずつ地球から遠ざかっていることを確かめたのである。

アメリカが月面に置いてきた鏡はコーナーキューブリフレクター(逆反射鏡)と呼ばれる反射鏡である。この反射鏡は三枚の平面鏡を互いに直角に張り合わせたもので、光が入射すると、平面鏡で三回反射され、反射光は常に入射光と平行になる。
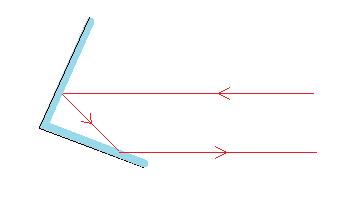
月が秤動と呼ばれる首ふり運動しているにもかかわらず、逆反射鏡を用いれば入射光と反射光は常に平行となり、反射光は地球に戻ってくることができるのである。逆反射鏡は我々の身近なところにも使われている。
自転車のペダルなどについている反射鏡をよく見ると蜂の巣状になっているのが分る。蜂の巣状に並んだ最小単位の一つ一つが小さなコーナーキューブリフレクターになっていて、車のヘッドライトが当たると、どのような角度で当たっても、その光を車の方に反射するので、運転手は自転車の存在を知ることができる。
月までの距離の測定は原理としては簡単であるが、ミリメートルの精度で計るその技術はたいしたものである。もし、これを読んでいる読者の部屋の横窓から月の光が差し込んでいるなら、読者から月まで距離は左右の目で既に数センチ異なっている。
地上の測定点から月の鏡までの距離は、月の軌道が楕円であることと、地球が自転していることによって時々刻々変化している。また、観測地点を乗せた大陸自体が年間数センチメートル移動している。
さらに、レーザーと逆反射鏡を用いても、発射された一回の光パルスのうち、月までの距離を往復して観測点に戻ってくる光の量は、極めて微弱なものであり、それを感知する高感度の検出器も必要となる。
永年加速
系の角運動量は保存するから、月の遠ざかる割合が分ると、地球の自転周期が伸びる割合が計算出来る。
地球の自転速度を基準にした地球時間は、潮汐摩擦のため、少しずつ遅れていることになる。日常生活には殆んど影響しない地球時間の遅れも、長期間の天体観測では無視できなくなる。前世紀の日月食のデータをもとにして、最近の日月食の起こる時刻を計算すると、実際に日月食の起きる時間は、昔のデータから計算した時刻より、早く起きることが知られている。これを永年加速という。
月が遠ざかり、その公転周期が長くなっているなら、日月食は月の公転周期が変化しないとして計算した時間よりも遅れて起こるはずである。それなのに、長期間における日月食の観測からは月の公転周期は逆にだんだん短くなっているようにみえるのである。この矛盾は時間の測定に地球時計を用いていたためである。月は遠ざかるため、その公転も遅くなっているにも拘わらず、測定に用いた地球時計がそれ以上の割合で遅れていくので、月の公転が見かけ上、逆に速まっているように観測されるのである。
現在では時間の計測に原子時計が用いられているので、地球の自転を基準にした世界時は原子時計で測った国際原子時から遅れることになる。そのまま放置しておくと、二つの時間の食い違いが累積されて大きくなり、日の出の時刻が遅れ、そのうち、極端に言えば、正午近くになって、寝ぼけた太陽が昇るようなことにもなりかねない。
この食い違いを補正するためには原子時計を時々遅らせて世界時に合わせる必要がある。そこで国際原子時に「うるう秒」を挿入した協定世界時が設けられている。うるう秒は一月一日か七月一日にとり入れるように決められている。うるう秒がとり入れられると、協定世界時でのその日の長さは二十四時間と一秒になる 。(うるう秒の導入についての定量的な説明は地球の自転と月の公転の項参照)
億万年の恋物語
地球と月の運動の変化はどこまで続くのだろうか。まず、太陽などの他の天体からの引力の影響はないものとして考えてみよう。運動の変化は潮汐摩擦によって引き起こされているのだから、潮汐摩擦がなくなれば運動は一定となるだろう。現在、地球の自転も月の公転もその周期はともに長くなっているが、長くなる割合は地球の自転のほうが大きい。
やがて、地球の自転周期が月の公転周期に一致すると、潮汐摩擦は無くなる。その状態では、月は静止衛星となり、地球の同じ場所の上空に照り、また月へ行って、そこから地球を見ると、地球はつねに片面だけしか見えないことになる。そうなると、鶴の求愛の舞のように、地球と月は互いに同じ面を向け合いながら、系の重心のまわりを運動することになる。天空に織りなす億万年の愛の進化である。月と地球の運動の‘進化’のように、愛もまた情熱という熱い血潮によって進化するのだろうか。

現在、月のほうは既に地球に同じ面を向けて運動している。地球で進行している、潮汐摩擦による自転の遅れは、すでに月では完了していることを示している。しかし、このことは、必ずしも、過去の月に水が存在していたことを示すものではない。地球が月に及ぼす起潮力は、月が固体であっても作用し、月を変形させるからである。
もし月が地球に同じ面を向けていなければ、月は、地球の起潮力のため、絶えず変形を繰返すことになり、内部摩擦によってエネルギーが消費され、月の自転も公転も変わることになる。もし、過去に月がぶよぶよとした液体状であったなら、内部摩擦によるエネルギーの消費は急速に進み、すでに遠い過去に、月は同じ面を地球に向けたのであろう。現在、月はその長軸を常に地球の方向に向けながら公転している。
他の天体からの力を無視すれば、地球と月の系の角運動量は保存しているので、地球と月が同じ面を向けて自転するようになると、月までの距離は一定に保たれるものと考えられる。しかし、太陽の存在まで考えると、地球は太陽からの起潮力も受けているので、その潮汐摩擦は地球の自転速度をさらに減少させ、地球と月は向かい合ったまま運動しながら、今度はその距離を減少させると考えられる。潮汐摩擦はエネルギーを散逸させているだけでなく、地球の自転、月の公転、太陽のまわりの公転、これらの運動の間にエネルギーと角運動量の受け渡しをおこなっているのである。
月の成因
潮汐摩擦のため地球と月の運動が変化していることを予言したのは、チャールズ・ダーウィンの息子のジョージ・ダーウィンである。さらに、彼は、月の成因について考え、月が遠ざかっているなら、過去へ時間を遡れば、地球と月が一体となっていた時代があったのではないだろうか。月は遠い過去に地球から生れたという説を唱えたのである。
地球が熔けてまだ液体状であったころ、太陽の潮汐作用によって地球の一部が引きちぎられ、月となって、地球の周りを回りはじめ、さらに月と地球は互に起潮力を及ぼし、潮汐摩擦によって月と地球の運動状態が変っていくと考えたのである。父親は生物における進化論を唱え、その息子は宇宙における進化論を唱えたのである。
月の成因説としては、かつて火星程度の惑星が地球に衝突し、その衝撃で地球から飛び出した物質から月が形成されたとするジャイアント・インパクト説が現在では有力であるが、大昔の月は今より地球に近かったのは確かである。その証拠は月の形状にも残されている。
現在の月の形状は僅かにラグビーボール状であるが、その変形の大きさを考えると、月が固まるまえの液体状の頃は、現在よりももっと大きな起潮力が働いていたと推測される。つまり、昔は地球に近かったために、当時の地球からの起潮力の大きさがその形状に残されたまま月は固まったのである。
軌道半径が短いと、公転周期、即ち、1ケ月の長さも短いことになる。さらに海の生物の成長は潮汐の影響を受けるので、サンゴなど海の古生物の化石を調べた結果、確かに数億年前の地球の自転は今よりずっと速かったことが知られている。
月の二分性
1959年、旧ソ連の無人月探査機ルナ3号は月の裏側の写真を送ってきた。人類が月の裏側を初めて見たときであるが、それは地球から直接見える表側の様子とはかなり異なったものであった。表側が比較的滑らか海が多いのに対して、月の裏側はクレーターの多い、でこぼことした表面であった。
月のクレーターの原因としては火山説と隕石説があるが、後者のほうが有力のようである。それなら、隕石は表より裏側に多く衝突したのだろうか。そうなら、その理由はなぜだろうか。
その後の月探査によって、さらに、月の地殻の厚さは表より裏のほうが厚く、その岩石の成分も表と裏では異なることがわかっている。もし、隕石の衝突頻度が表と裏で同じなら、表側の隕石痕のみが内部から流れ出た溶岩によって消されたのだろうか。
月をめぐる謎はつきないが、このような月の表と裏の違いを月の二分性と呼び、その原因はまだ明確には分かってはいない。月の成因やその進化の過程を解く鍵として、最近打ち上げられた日本の月探査機「かぐや」からの今後の観測データが、期待されている。
月と生命と文化
あらゆる生命は太陽の恩恵を受けて生きている。太陽なしでは地球上の生命は生まれることも生き長らえることもできなかったであろう。生命に対して果たしている役割では、月は太陽に到底及ばないが、月も、とくに海の生き物に対しては潮汐を通して、産卵や脱皮などに少なからぬ影響を及ぼしているようである。
さらに、月は、太古の昔、生命の起源にも大きな役割を果たしたと考えられる。生命が地球に初めて現れた三十八億年前、月は地球に近く、地球の自転は速く、太古の海は激しい潮汐で荒れていたに違いない。最近では、地球の最初の生命は、海岸に打ち寄せる波がつくる水の泡の、その膜のなかで生まれたという説が有力視されている。
月の起潮力は地球の自転軸の歳差運動にも作用を及ぼすので、月の存在は地球気候の長期的な変動の原因ともなっている。自転軸の向きが変わることによって、日射量の分布が変わるからである。もし、月がなかったなら、生命の進化も、現在の地球の気候もずいぶん変わっていたと思われる。太陽が生命の誕生や存続に文字通り陽の役割をしているのに対して、月は陰の役割をしているようである。
月はまた我々の文化にも多くの影響を与えている。童謡、童話、神話、宗教、伝説、詩、小説、絵画などの人間の精神文化に果たした役割では、むしろ、月のほうが太陽よりも大きいのではないだろうか。
逆行衛星
通常、惑星の自転の向きとその衛星の公転の向きは同じであるが、海王星の衛星であるトリトンの公転の向きは海王星の自転の向きとは逆向きである。トリトンのような逆行衛星では、潮汐摩擦のため、衛星の進行方向と逆向きの力が働き、軌道運動は力学的エネルギーを失い、軌道半径が徐々に小さくなると考えられる。
トリトンが海王星に近づくと益々起潮力が大きくなり、エネルギーの散逸も増すので、トリトンの公転軌道は極めて不安定である。このような不安定な逆行衛星が太陽系の形成時から、海王星のまわりを回っていたとは考えにくい。これがトリトンはあとで海王星の引力に捉えられて、その衛星になったと考えられる所以である。 トリトンが外部から海王星の引力圏に迷い込んだのであれば、その公転軌道は離心率の大きな楕円と考えられる。実際、太陽系の外縁部に存在するオルトの雲と呼ばれる彗星の巣から、太陽の引力圏に落ち込んでくる彗星の軌道は双曲線か放物線か離心率の大きな楕円である。しかし、トリトンの公転軌道はほぼ完全な円である。
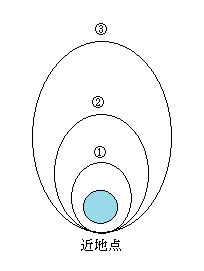
その理由を考えるために、図6のように、初め楕円軌道①を回る人工衛星が近地点で進行方向に撃力を加えると、地球を一周した衛星は近地点に戻るが、軌道は別の楕円②や③となる。逆に楕円軌道③を運動している衛星に近地点で進行方向と逆向きに撃力を加えると、衛星はエネルギーを失うが、近地点は変わらず衛星の軌道は円に近づく。
楕円軌道に打ち上げられる探査衛星は、ごく薄いながらも上空の大気との摩擦によって、主に近地点でエネルギーを失うため、軌道の形は円に近づき、摩擦がさらに増し、短期間に落下する。
トリトンの軌道もおそらく最初は大きな離心率を持つ楕円であったろう。たまたま、海王星の自転と逆向きに公転することになったトリトンは潮汐摩擦により後ろ向きの力を受けエネルギーを失うことになるが、それは近地点で大きいため、トリトンの軌道は完全な円となったのであろう。
トリトンの軌道の離心率が0であるのに対して、地球の衛星である月の軌道の離心率は0.055で、同程度の質量を持つ他の衛星と比べると、大きな離心率である。月の場合も潮汐摩擦による力は近地点で大きく、その向きは月の進行方向なので、月の軌道の離心率は、トリトンの場合とは逆に、大きくなっていると考えられる。
今後、トリトンは、円軌道を保ったまま、その軌道半径を小さくしていくが、海王星に落下する前に、今度は海王星がトリトンに引き起こす起潮力のため、引き千切られ、海王星のまわりを海王星の自転と逆向きに公転するリングになるかも知れない。
惑星リングは太陽系の惑星では、木星、土星、天王星、海王星に存在するが、現在まで、惑星の自転と逆向きにまわるリングは発見されていない。惑星に近すぎたため、惑星の起潮力が大きく、衛星になれなかった小物体が衝突と摩擦を繰り返し長い時間をかけて形成されたものが惑星リングであろう。惑星リングは摩擦や衝突によるエネルギーの散逸によって出来上がった安定な究極の構造であろう。
尽数関係
太陽系の一番内側の惑星は水星である。水星の軌道運動には僅かな近日点移動が観測されている。かつて、水星の内側にもう1つ、未発見の惑星があり、その作用で水星の近日点移動がおこると考えられたこともあった。その後、アインシュタインの一般相対性理論によって、水星の近日点移動は説明され、水星より内側の惑星の存在も現在では否定されている。
一般相対性理論の検証に重要な役割を果した水星の軌道運動であるが、一方、自転運動のほうは、強い太陽光線のためにその周期の測定は困難であった。太陽からの強い起潮力と、そのためにおこる潮汐摩擦のため、水星も太陽に同じ面を向けて公転しているものと考えられていた。しかし、最近では、水星の自転周期も測定され、図7のように水星は1回公転する間に1回半自転することが分っている。
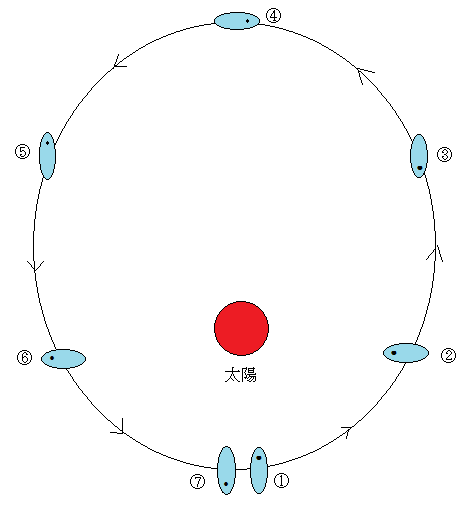
水星から見た日の出、日の入りを考えてみると面白い。太陽からの起潮力が大きい近日点①では、水星は長軸を太陽方向に向け、このとき太陽に面している側は、水星が太陽の周りを公転し、再び近日点⑦に戻ってくると、太陽と反対側にきて深夜となる。つまり水星は太陽のまわりを二周して、もとの位置に来たとき南中時を迎える。水星では、一日の長さと二年の長さが等しいという奇妙な結果となる。
月や水星の場合のように、天体の公転周期や自転周期の間の比が簡単な整数比をとることを尽数関係という。水星の場合の自転周期と公転周期の尽数関係が1:1でなく、2:3であるのは、水星の軌道が0.21と大きな離心率を持つ楕円軌道だからである。
厳密には自転の角速度も、太陽からの起潮力のため、わずか脈動してはいるものの、ほぼ、一定であるのに対し、公転の角速度は、楕円軌道のため、一定の値をとれず、近日点では大きく、遠日点では小さくなる。そのため、水星は同じ面を常に太陽の方向に向けていることが出来ないのである。
水星は、起潮力が一番大きくなる近日点では、その長軸を太陽方向に向けているが、1回公転するごとに、表と裏を交互に太陽に向けることになる。
尽数関係は天体運動における一種の共鳴現象であり、地球と月の系、太陽と水星の系、以外にも、惑星どうしの系や、惑星リングと衛星からなる系など、天体のいろんな系で、潮汐摩擦によってつくられた現象であるが、複雑で不思議に思える現象も分かってしまえば、その仕組みは極めて理にかなったものである。
潮汐理論との出会い
月の裏側はなぜ見えないのだろうか?この魅惑的な問題に初めて出会ったのは小学校の6年生のとき、理科の授業のときであった。月の自転と公転の周期がぴったり一致しているからだと、先生は教卓のまわりをぐるりと一回りし、実演して教えてくれたことを記憶しているが、それは月の裏側が見えないことを単に言い換えたに過ぎない。つまり、月の裏側がなぜ見えないかではなく、なぜ、見えなくなったのか、その理由を知りたかったのだが、当時の筆者には考えてもその答の見当さえつかなかった。
しばらく忘れていたその疑問に答を見つけたのは、大学に入学した直後、学生運動をしていた友人から勧められて買ったエンゲルスの「自然弁証法」という文庫本 を何気なくめくっていたときのことであった。
当時、定価150円のその本のなかに、潮汐摩擦という4文字を見つけた瞬間、目から鱗が落ちる思いであったが、それと同時に、筑後川のほとりに生まれながら、毎日、潮の干満を見て育ちながら、さらに、物理を志しながら、小学、中学、高校と、潮汐摩擦に考えが及びつかないまま過ごした自分の愚鈍さに気づき、衝撃を覚えたものである。

コメント