仕事のパラドックス？

　ペダルを踏み自転車を加速するとき、仕事をするのは人の筋力か？それとも自転車の後輪が道路から受ける水平抗力か？
　芥川龍之介の短編小説「蜘蛛の糸」に端を発した仕事の問題も1）、30数年前にアメリカで発表された論文2）によって、既に‘不可逆的に’解決済みだとして、筋力説を主張する常識派に対し、執拗に抗力説を主張し論争を挑むのは、常識や先入観に囚われず、自ら考え行動せよという先人の教えを守り、些か常識の欠落した人生を歩んできたという脱常識派。
　戦前の予想は、脱常識派にとって圧倒的に不利。だが、明るいニュースもある。助けた蜘蛛に頼んで占ってもらったところ、脱常識派の勝利と出た。いよいよ雌雄を決する時はきた。両軍サポーターが固唾を飲むなか、キックオフの笛がピッチに響き、論戦の火蓋は切られた。脱常識派：前輪に働く後ろ向きの水平抗力は小さいので、これを無視すれば、人と自転車からなる系に働く外力は、後輪が道路から進行方向に受ける水平抗力（静止摩擦力）のみである。系の並進運動に仕事をするのも水平抗力しかない。
常識派：水平抗力は作用点が動かないので、仕事をするはずはない。これは力学の常識。仕事をするのは自転車に乗っている人間の筋力。これは世間一般の常識。抗力説はどちらの常識にも反する。
脱常識派：人と自転車の系にとって筋力は内力だから、系の並進運動に仕事をしない。宇宙飛行士が無重力空間で、いくら手足を動かしても、外力なしでは、前に進むことはできない。
常識派：道路から受ける水平抗力が仕事をしてくれるなら、人は疲れず楽だが、それは日常の経験に反する。
脱常識派：筋力は一切仕事しないというのではない。並進運動に仕事をすることはできないが、自転車の後輪にとって、筋力は外力であるから、ペダルとチェーンを介して後輪の回転運動に仕事をすることができる。一方、水平抗力は、並進運動にとっても、後輪の回転運動にとっても、外力であるから、両方の運動に仕事をする。ただし、水平抗力は、並進運動に正の仕事をしているが、後輪の回転運動には負の仕事をしている(下の表参照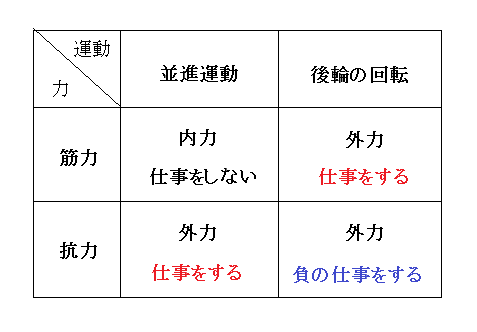）。　水平抗力のなす正負同時一対の仕事によって、後輪の回転エネルギーが、系の並進運動のエネルギーに転換される。結果として系全体の運動にエネルギーを供給したのは筋力だから、当然、自転車のペダルを踏めば、我々、脱常識派も、常識派の人間と同じく疲労する。
常識派；それなら、並進運動に仕事をしたのも筋力ということになるではないか。
脱常識派：推進力である水平抗力を生みだすのは筋力だが、筋力が直接並進運動に仕事をするのではない。系の運動は、並進運動とそれ以外の運動に分けて考えることができる。並進運動のみに仕事をしたのは水平抗力である。
　エネルギーの起源を遡れば、並進運動のエネルギーも、筋力のエネルギーに違いないが、エネルギーを供給しても、それを仕事をしたとは言わない。筋力のエネルギーも、起源は体外から取り入れた食物のエネルギーであり、さらにその起源も太陽エネルギーである。究極まで遡れば、宇宙のビッグバンということになるが、137億年前のビッグバンが仕事をして自転車や車が走っているとは言わない。筋力からエネルギーの後方支援を受けて水平抗力が並進運動に仕事をしたのである。但し、筋力のエネルギーが一旦道路に蓄えられるのではない。水平抗力が、並進運動と回転運動に正負同時一対の仕事をすることによって、筋力のエネルギーを、後輪の回転運動を経由して並進運動に供給している。水平抗力自身はエネルギーを創り出さないが、並進運動に仕事をしたのは水平抗力である。
常識派：岩波書店の理化学辞典には、仕事を次のように定義している。「力学系に力F が作用し、作用点がdr だけ変位するとき、スカラー積F・dr を、その力が力学系になした仕事という。」これは、作用点の動かない抗力が仕事をすることを禁じている。
脱常識派：仕事は理化学辞典の定義だけではない。同じ岩波書店の広辞苑では次のように定義されてしている。「力が働いて物体が移動した時に、物体が移動した向きの力と、移動した距離との積を、力が物体になした仕事という。」簡単のため、今後、広辞苑で定義されている仕事を仕事A、理化学辞典の仕事を仕事Bと呼ぶことにしよう。仕事には仕事Aと仕事Bとがある。
常識派：仕事には仕事Bしかない。仕事Aは物体が質点のとき、あるいは質点と見なせるときの仕事であるから、仕事Bに含まれる。
脱常識派：高校の物理教科書も仕事の定義は広辞苑と同じく仕事Aである。仕事Aが、質点に対する仕事なら、高校物理で扱う物体は質点のみに限られることになるが、高校で習うのは質点の力学だけではない。仕事Aは一般の物体の並進運動に外力がなす仕事と考えるべきである。
常識派：30数年前にアメリカで発表された論文2）では、仕事Bだけが真の仕事（real work)だとしている。力と物体の重心の移動距離との積はpseudoworkであり、これは仕事に似ているが、本物の仕事ではない。水平抗力が一見仕事をしているかのように思えるが、それは偽物の仕事であり、真の仕事をするのは筋力である。
脱常識派：その論文においてpseudoworkと呼んでいる仕事は、本当は並進運動になす真の仕事、仕事Aである。系内に動力源が存在しない場合（参考資料）にも、仕事Aと、抗力のなす正負同時一対の仕事とが必要なのは明らかである。
常識派：自転車を加速できるのは水平抗力が仕事をするからではなく、水平抗力が自転車に力積として働き、人と自転車からなる系の運動量が増加するからである。仕事をして系の運動エネルギーを増加させるのは筋力であり、系に並進運動を引き起こすのは、抗力による仕事ではなく、抗力の力積である。
脱常識派：系に作用する力積も、系の並進運動にする仕事も、どちらも並進運動に対する運動方程式から導かれるので、力積に寄与する力と、仕事に寄与する力とは同じでなければならない。両者の力が異なると、木に竹を継ぐことになる。仕事Aも仕事Bも真の仕事でなければ、整合性は保てない。
　系全体の運動に仕事をするのが仕事Bであり、そのうち系の並進運動にする仕事が仕事Aであるが、物体の並進運動を扱うことのない熱力学や材料力学では仕事Aは必要ではない。しかし、自転車や人が走る場合のように、内部運動が存在していても、並進運動を第一義的に扱う場合は仕事Aが重要になる。
　仕事の定義も運動方程式に則ったものでなければならない。古典力学は既に完成した学問であり、そこにパラドックスは存在しない。不可解な偽物の仕事などが迷い込む隙もない。古典力学ではニュートンの三つの運動法則が最優先であり、アメリカ　ファーストではない。
常識派：それでは、筋力が仕事をして自転車は走ると言ってはいけないのか。
脱常識派：日常会話ならそれで差し支えはなかろう。しかし、力学では、筋力が仕事をすることができるのは、並進運動ではなく、後輪の回転運動に対してである。筋力の仕事だけでは、並進運動にエネルギーを伝えることはできない。仕事Aと抗力のする正負同時一対の仕事が必要になる。日常用語としての仕事と物理用語としての仕事は一般には異なる。物理用語を無理に日常用語に合わせようとすると、整合性がとれなくなる。抗力は一切仕事をしないとして、仕事Aを真の仕事から排除したために生じた矛盾をとり繕おうとして不用意に導入したpseudoworkが、さらなる混乱を招いたようである。
常識派：抗力が仕事をすると考えると、力学教育が混乱しないか。
脱常識派：Pseudoworkが登場する前の正常な状態に戻るだけだから、むしろ混乱はなくなる。現行の教科書や辞典の、仕事についての記述も昔のままであるから、‘可逆的に’戻ることに何の障害もない。
参考文献
1）後藤信行：「蜘蛛の糸」仕事をしたのはカンダタの筋力か？　日本物理学会誌　Vol. 71, No. 2, （2016）　
2）Bruce Arne Sherwood： Pseudowork and real work, , Am.J. Phys.,Vol.51, 1983
[参考資料]
抗力のする正負同時一対の仕事

　図のように、半径 ${ a }$ 、質量 ${ M }$ 、中心軸のまわりの慣性モーメント ${ I }$ の円柱を考え、円柱に巻きつけた糸を、右方向に引っ張り、円柱を水平な床の上で転がしてみよう。
　糸の張力を ${ T }$ 、円柱が床から右方向に受ける水平抗力（静止摩擦力）を ${ F }$ 、円柱の重心 ${ G }$ の座標を ${ x }_{ G }$ 、円柱の右回りの回転角をθとする。円柱の重心の並進運動および回転の運動方程式は、それぞれ、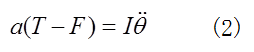となる。ここで、円柱に働く水平抗力の向きが気になるが、円柱の慣性モーメントは、 $M{ a }^{ 2 }/2$ であるから、(１)と(２)より、F=T/3 となる。水平抗力は、張力と同じく、図のように、右向きに働くことが分かる。
　力の作用点Ｐを微少距離 $d{ x }_{ P }$ だけ右に変位させたとき、重心Ｇの変位を $d{ x }_{ G }$ 、角度θ の変位をdθ とすれば、 $d{ x }_{ P }=2d{ x }_{ G }$ 、および、 $d{ x }_{ G }=ad\theta$ が成り立つ。
（1）の両辺に $d{ x }_{ G }$ をか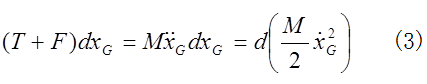ければ、　また、（2）の両辺に $d{ x }_{ G }$ をかければ、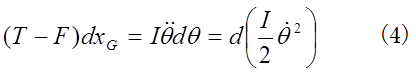となる。
　（3）式の右辺は円柱の並進運動のエネルギーの増し分であるから、左辺は力（Ｔ＋Ｆ）が円柱の並進運動にした仕事であり、広辞苑の定義に一致する。また、（4）式の右辺は回転運動のエネルギーの増し分であるから、この式の左辺は力（T-F)が円柱の回転運動にした仕事である。張力Ｔは並進運動と回転運動の両方にTdx_Gの仕事をするのに対し、水平抗力Ｆは重心運動にＦdx_G の仕事をし、回転運動に-Ｆdx_G の仕事をしている。つまり、抗力は、並進運動と回転運動に、正と負一対の仕事を同時にしている。
　円柱に働く外力(T+F) は円柱の並進運動に仕事をし、そのエネルギーを増すとともに、円柱に力積を及ぼし、円柱の並進運動の運動量を増している。つまり、並進運動のエネルギー増分も運動量の増分も、重心の運動方程式（１）式から導かれるので、並進運動に仕事をする力と力積に寄与する力はどちらも（1）式の左辺の力T+Fである。
　（3）と（4）を加えると、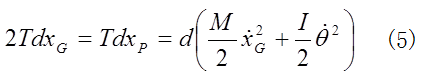
となり、これは理化学辞典の定義に一致する。（3）式の仕事には、抗力も含めたすべての外力が寄与するが、円柱全体の運動にする仕事（5）式には、作用点が動かない水平抗力は現れない。
　運動方程式(１)と(２)から、先に、F を消去すれば、(３)と(４)式を経由せずに(５)式が直接導かれるが、抗力F のなす正負同時一対の仕事が隠れてしまい、抗力Fの役割も分からない。