黄金分割とフィボナッチ数列

最も美しい長方形
　
　図のように長方形ABCDから長方形の短辺ABを辺とする正方形ABFEを切り取ったとき、残りの部分の長方形DEFCがもとの長方形ABCDと相似になるとき、長方形ABCDの長辺ADと短辺ABの比を黄金比と呼ぶ。黄金比の長方形は古代から最も美しい長方形とされている。

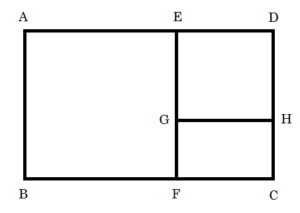
　左図の黄金比長方形ABCDにおいて、ABの長さを1、BC=xとすれば、長方形ABCDと、長方形DEFCとが相似だから、1:x=(x-1):1である。これから二次方程式；
　　x²-x-1=0　　　(1)
が導かれ、これを解けば、
x=(1±√5)/2
となる。正の解をφとすれば、
φ＝(1+√5)/2＝1.6180339887…となる。φが黄金比である。


　　　　　　　　　　　　　　　　　　　　　　＝・・・・・・
のように連分数で表わされる。
フィボナッチ数列
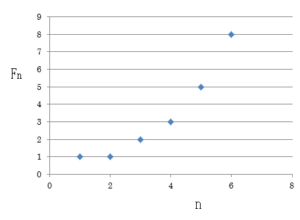
　数列；　1,　1,　2,　3,　5,　8,　13,　21,　34,　55,　89,　144,　233,　・・・をフィボナッチ数列という。
　n番目の数をF_nとすれば、フィボナッチ数列は次の規則で作られている。、
　　　　　　　　　　　　
　　　　　　　　　　　　F₁＝F₁＝1　　　　　　　　　（2）
　　　　　　　　　　　　F_n+1＝F_n+F_n-1　　　　　　　（3）
　フィボナッチ数列の各項を奇数と偶数の配列として考えると、
　　　　　　　　　　　
　　　　　　　　　　　　奇奇偶奇奇偶奇奇偶奇奇偶奇・・・
となる。つまり、奇奇偶の繰り返しであるが、これはフィボナッチ数列の規則（2）と（3）をから明らかであろう。

　（3）式の両辺をF_nで割ると、
　　　　　 F_n+1/F_n＝1+F_n-1/F_n 　　　　　　　(4)
nが十分大きいとき、F_n+1/F_n→ｘとすると、（4）式は、
　　　　　　　　　x=1+1/x　　　　　　（5）
となるが、これは方程式（1）と同じである。即ち、nが十分大きくなると、フィボナッチ数列は黄金比φを公比とする等比数列に近づく。