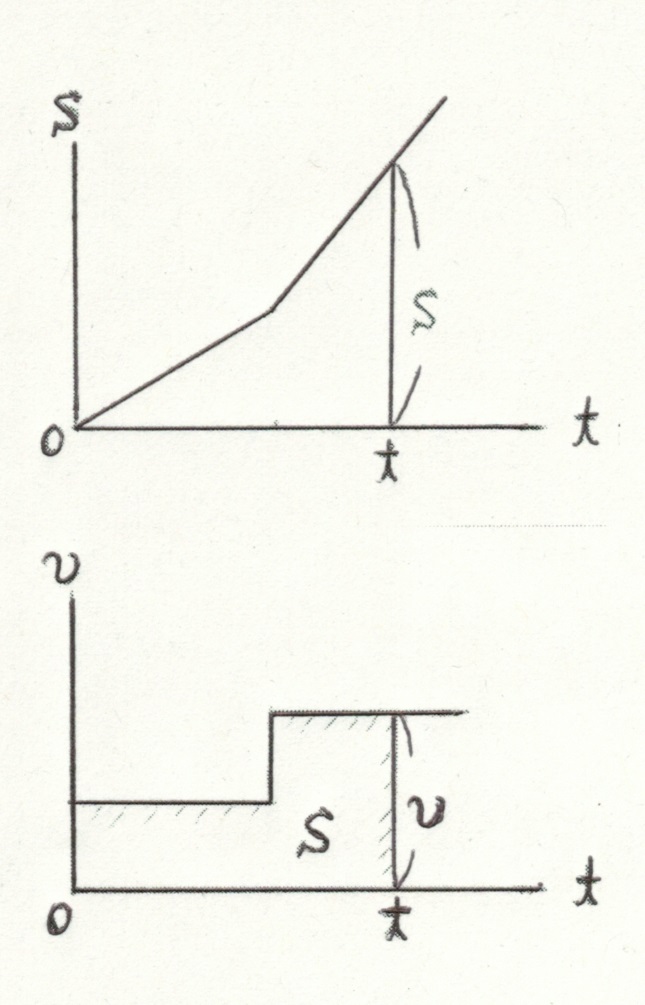
 健康機器のルームウォーカーには、開始してからの経過時間と速度と距離が計器上に表示される。速度は使用途中でも手動ボタンを用いて変更できる。最初、ある速度に設定し、しばらく時間が経過したあと、速度を上げたとすると、距離Sの時間tに対するグラフ、S-tグラフを描けば折れ線グラフとなろう。折れ線の折れ目の時刻が速度を切り替えた時刻であり、折れ線の傾きのそれぞれが切り替えた前後での速度Vになる。
健康機器のルームウォーカーには、開始してからの経過時間と速度と距離が計器上に表示される。速度は使用途中でも手動ボタンを用いて変更できる。最初、ある速度に設定し、しばらく時間が経過したあと、速度を上げたとすると、距離Sの時間tに対するグラフ、S-tグラフを描けば折れ線グラフとなろう。折れ線の折れ目の時刻が速度を切り替えた時刻であり、折れ線の傾きのそれぞれが切り替えた前後での速度Vになる。
次に、この場合の速度計の変化のグラフ、V-tグラフは明らかであるが、ある時刻tにおける距離計の示す数値Sは、このV-tグラフにも、斜線で示された部分の面積として現れる。つまり、S-tグラフの傾きからV-tグラフが得られ、逆にV-tグラフにおける高さVが、その時刻までに掃く面積からS-t グラフが得られる。
S-tグラフからV-tグラフを求めることを微分、逆にV-tグラフからS-tグラフを求めることを積分という。つまり、距離Sを時間tで微分すれば、速度Vとなり、逆に、速度Vを時間tで積分すれば距離Sになる。
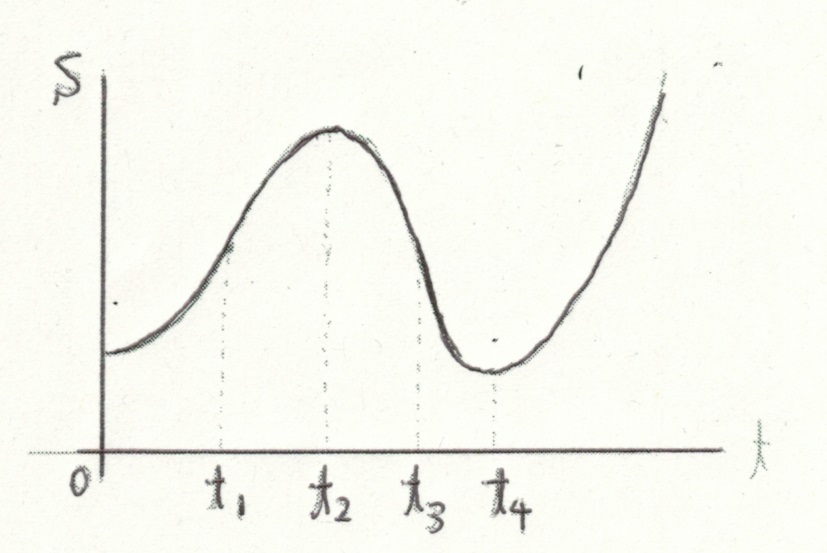 これはルームウォーカーの速度を小刻みに、かつ、こまめに変えたときにも言える。その場合には、二つのグラフはともに連続で滑らかな曲線に近づくだろう。S-tグラフが滑らかで連続な曲線の場合、ある時刻における速度は、その時刻における グラフの接線の傾きとなる。
これはルームウォーカーの速度を小刻みに、かつ、こまめに変えたときにも言える。その場合には、二つのグラフはともに連続で滑らかな曲線に近づくだろう。S-tグラフが滑らかで連続な曲線の場合、ある時刻における速度は、その時刻における グラフの接線の傾きとなる。
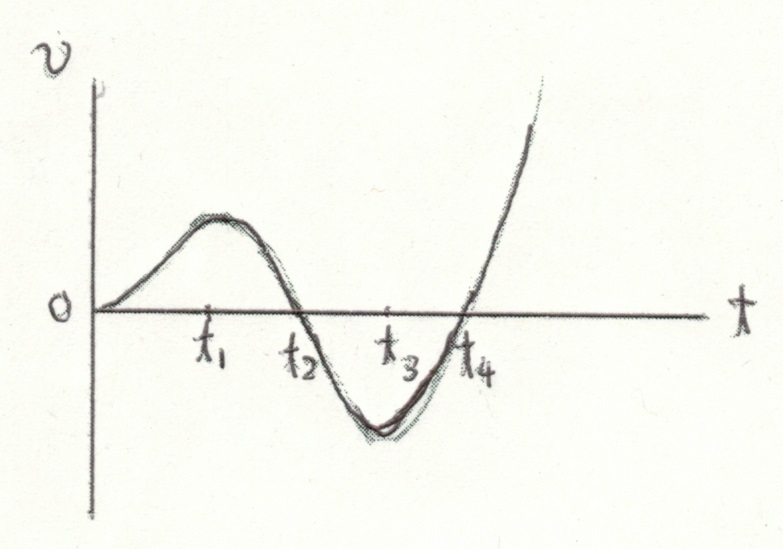
このとき、S-tグラフが与えられると、v-tグラフは一意的に決まるが、逆にv-tグラフが与えられたとき、それを積分したS-tグラフは一意的には決まらない。S-tグラフに任意定数を加えても、接線の傾きは変わらないので、任意定数を加えたS-tグラフを微分して得られるv-tグラフは、加えた任意定数に関係なくどれも同じになるからである。この任意定数を積分定数と呼ぶ。
与えられたv-tグラフからS-tグラフを求めるには、積分定数を求めなければならないが、それには初期条件が分かっていなければならない。
ルームウォーカー
 数学
数学
コメント