奇妙な回転
剛体の運動は並進運動と重心のまわりの回転運動に分離して考えることができる。剛体に外力が一切働いていなければ、並進運動は、慣性の法則により、重心が静止したままか、等速度運動するかのどちらかである。一方、回転運動に対しては、角運動量保存則によって、角運動量は、その大きさも方向も一定に保たれる。しかし、無重力空間で物体を回転させると、物体が一見、角運動量保存則に反するかのような、奇妙な回転をすることがある。
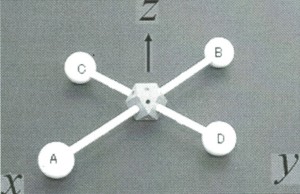
無重力空間でなくても、同様な回転を地上で実現させることができる。例えば、化学教育で用いる分子模型で図1のような剛体をつくる。ただし、球AとBの間隔を球CとDの間隔より長くしておく。ここで、物体に固定した座標軸を図1のように選ぶ。つまり、球Aの方向をx軸、球Dの方向をy軸とし、その2軸に垂直にz軸を選ぶ。この模型を回転させながら空中に放り投げてみよう。z軸やx軸のまわりに回転させると、安定に回転するが、両手の指で球Cと球Dを摘まんで、y軸のまわりに回転させながら投げると、複雑な回転になることが分かる。分子模型でなくても身近にあるカマボコ板や台所のしゃもじでもよいが、板状のものは軽いと空気の抵抗が無視できないので、ある程度、重さがあるほうがよい。しかし、スマホやリモコンは投げないほうがよいだろう。屋外での実験ならテニスラケットを高く投げるとよい。
剛体の回転主軸
一般に剛体は三つ慣性主軸を持つ。図1の剛体では、その慣性主軸は、x、y、z軸であり、その三つの軸のまわり慣性モーメントをそれぞれ、Ix, Iy, Izとすると、球ABの間隔が球CDの間隔より長いので、 Ix< Iy< Iz となる。x軸は慣性モーメントが最小の軸であり、z軸は最大の軸、そしてy軸は慣性モーメントの大きさが中間の軸である。中間軸のまわりの回転は不安定になるが、これは「テニスラケットの定理」とも呼ばれている。図1の模型やテニスラケットやカマボコ板のように、三つの主軸のまわりの慣性モーメントの値が三つとも異なる物体、いわゆる三軸不等の剛体の自由回転を理解するには、剛体の回転の運動方程式を解かなければならないが、ここでは、もう少し簡単な説明を試みてみよう。
角運動量とエネルギーの保存則
外力が働かない剛体の自由回転では、角運動量と回転の運動エネルギーが保存しなければならない。つまり、角運動量の大きさをL、その成分をLx 、Ly 、Lz とし、回転のエネルギーを Eとすると、二つの保存則は、それぞれ
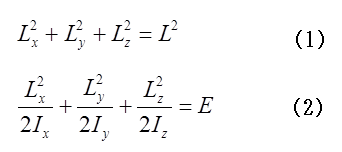
と表すことができる。Ix、Iy、Izは剛体に固有な定数であり、L2とEは一定ででなければならない。(1)式および(2)式は、剛体に固定した、xyz座標系において、角運動量ベクトルLの先端Pが球面(1)および楕円体面(2)の面上になければならないことを示している。つまり、二つの曲面の交線が点Pの辿る軌跡となる。角運動慮Lは、空間に対しては一定であり、その先端Pも空間に対しては定点であるが、物体に固定された座標系から見れば、Lの先端Pは、(1)式で表される球面上に描かれた等エネルギー線上を動くことになる。
等エネルギー線のトポロジー
角運動量Lの先端Pは、球面(1)と楕円体面(2)の交線上を巡るので、交線は球面上に描かれる等エネルギー線となり、それは球面上に閉曲線を描くことが分かる。
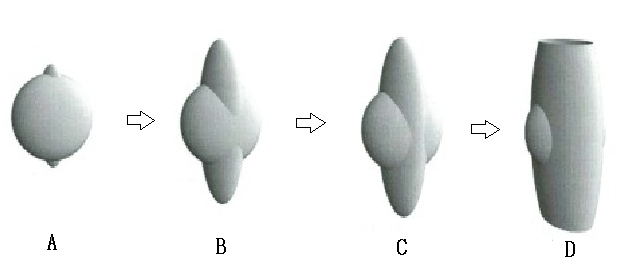
球面(1)の半径Lは一定であるから、等エネルギー面を表す楕円体面(2)式のEを増していけば、二つの曲面は図2のように、A→B→C→Dのように変化する。二つの曲面の交線、つまり、等エネルギー線は、図Aでは物体のz軸のまわりに小さな閉曲線を描き、エネルギーが増すと、その閉曲線は大きさと形を変え、Bになり、BからCになる途中で、z軸を囲む閉曲線から、x軸を囲む閉曲線に変わり、さらにエネルギーが増せば、その閉曲線はD図のように小さくなる。
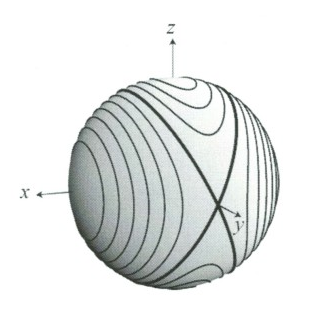
等エネルギー線を表す閉曲線群を一つの球面上に描くと、分かり易い。図3のように、z軸とx軸を囲む閉曲線は存在するが、中間軸のy軸を囲む閉曲線は存在しない。
この図において、球面とz軸およびx軸との交点は、それぞれエネルギーEが最小と最大の状態に対応し、それらの軸を囲む等エネルギー線が存在するが、球面とy軸との交点はサドル点となり、y軸を囲む等エネルギー線は存在しない。等エネルギー線のうち、y軸上で交差する二つの大円は軌道運動に対するヘテロクリニック軌道であり、球面上の等エネルギー線の族を、x軸を囲む閉曲線とz軸を囲む閉曲線とに分割するセパトリックスである。
剛体の第一軸(z軸)および第三軸(x軸)のまわりの回転は、その軸を囲む等エネルギー線が存在し、安定な回転となるが、第二軸(y軸)のまわりに回転させようとすると、それを囲む等エネルギー面が存在しないため、角運動量ベクトルの先端の軌道はヘテロクリニック軌道近くをめぐり、y軸とマイナスy軸に交互に接近することになる。これは、図1の模型をy軸の周りに回転させようとすると、球Cと球Dが入れ替わりながら回転することを意味している。球Cと球Dの一方を着色しておけばその様子が分かりやすい。(図2および図3は、長崎大学冨塚明氏による計算ソフト、マセマチカを用いての作図)
極運動
地球は完全な球ではなく、少しだけ南北方向が短い。そのため、地球の形状から決められる極点(慣性主軸のz軸が地球表面を貫く点)のまわりに自転軸が直径10m程度の円を描きながら約430日周期でまわっている。これは図2のA図に相当し、それは地球の自転軸の向きが変化しているのではなく、自転軸のまわりに極が動いている。これを地球の極運動と呼ぶが、これは地球の磁極が動く極移動ではなく、力学的に決まる地球の極の運動である。
月面宙返り
鉄棒競技の着地「月面宙返り」でも、鉄棒から離れる瞬間、選手の体は中間軸(左右軸)に回転しながら空中に投げ出される。カマボコ板を中間軸(y軸)のまわりに回転させながら投げるのと一緒である。ただし、カマボコ板の自由回転では、角運動量もエネルギーも保存し、さらに、カマボコ板は変形できないので、慣性楕円体の形状も一定である。しかし、月面宙返りの場合は、選手に外力が働かないので、角運動量は保存しているが、選手が体を変形させることによって、慣性楕円体の形状もエネルギーも変化させることができるので、さらにもっと複雑な回転が可能となる。
つぶやき
本当は、ラケットやカマボコ板でなく、録画onの状態にしたスマホを投げれば、体操の金メダリストが見た景色を録画できるかもしれない。しかし、それは、やはり、やめておこう。スマホが目を回して壊れるかもしれないので・・・

コメント
「多軌道による重力回転装置」を考案しました。
ブログを見ていただければと思います。
ブログ「夢のエコ発電」https://nakaei.at.webry.info/202109/article_1.html