どちらが重いか?
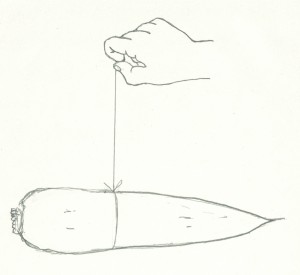
昔から知られた問題だが、図1のように、大根を糸で吊るし、釣り合うところで大根を二つに切れば、切り離された二つの重さは等しいだろうか。つい、同じと答えたくなるが、実際には太い側のほうが重い。釣り合っているのは、左右の重さではなく、左右の力のモーメントだからである。大根の重心は吊るした糸の延長線上にあるが、一般に、重心を含む平面で、物体を切ったとき、切り分けられた二つの部分の質量は等しいとは限らない。大根のかわりに三角形の一様な薄い板を考えてみよう。
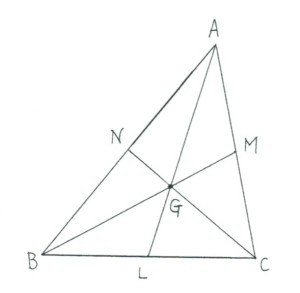
中学の数学によれば、図2のように、三角形の頂点とその対辺の中点を結ぶ直線を中線とよぶと、三本の中線は一点で交わり、その交点が重心であり、⊿ABCは三本の中線によって、6個の三角形に分割されるが、それらの面積は全て等しい。よつて中線は重心によって2:1の長さに内分される。さて、重心を通る直線で三角形を切り離したとき、三角形の面積を二等分するのは、三本の中線のいずれかで切ったときのみであり、もし、重心を通り、ひとつの辺に平行な直線で切れば、切り離された両者の面積は4対5となり、その辺を含む側が大きくなる。ちなみに、直円錐をその重心を含み、軸に垂直な面で切ったときの体積比は37対27となる。
チキリとシーソー
力のモーメントの釣り合いを利用して重さを測る道具に、昔、図3のような竿秤(さおばかり)があった。ちぎばかり(千木秤、杠秤)とも言い、九州地方ではチキリと呼ばれていたが、竿に目盛が刻んであり、釣り合ったときの分銅の位置から重さが分かる仕組みである。
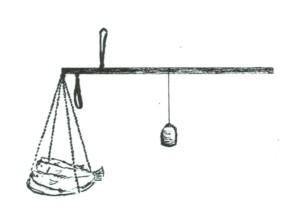
薬の調合などに使われる上皿天秤は、左右対称であり、薬と分銅の重さの釣り合いから重さを計る。一方、非対称な竿秤は力のモーメントを釣り合わせて重さを計るのであり、計量している物の重さと分銅の重さが等しいのではない。上皿天秤が多くの分銅を必要とするのに対し、竿秤は、分銅の位置によって力のモーメントを加減できるので、一個の分銅しか必要とせず、上皿天秤に比べ、精度は劣るが、持ち運びが簡単であり、昔は行商でよく使用されていた。
最近では、事故のときの管理責任が問われることを恐れてか、シーソーのある公園が少なくなっているようだが、ギッコンバッタンいう名で親しまれたシーソーは、チキリとともに、力のモーメントや、「梃子(てこ)の原理」をこどもが無意識のうちに学ぶのに、格好の教材でもあった。シーソーに、親子で乗って遊ぶとき、体重の重い親は支点の向こう側に乗った子供に比べ、より支点に近づいて乗らなければならない。それぞれの体重の力のモーメントが親子で等しければ、シーソーは釣り合う。力のモーメントとは力の大きさと、支点から力の作用線までの距離の積で表される。
梃子とアルキメデス
チキリもシーソーも梃子の原理が使われているが、梃子について、最初に考察したのは、浮力の原理でも知られるアルキメデスと言われている。「我に支点を与えよ、されば地球をも動かしてみせん」という有名なことばを残した彼は梃子の原理を、対称性の理から導いたという。左右対称な天秤の原理から、一般には非対称な竿秤の原理を導いたというのだが、その証明法は次のとおりである。
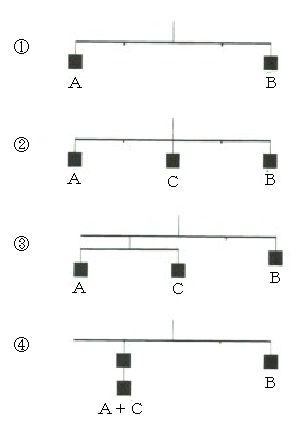
まず、重さの無視できる棒と、長さがその半分の短い棒、重さがWの三つの重りA、B、およびCがあるとしよう。図4の①のように、長い棒に、重りAとBを支点から等距離のところに釣り下げれば、釣り合うことは自明であろう。左右対称であるから、棒がどちらかに傾く必然性はないからである。これを天秤の原理と呼ぶことにしよう。
次に、②のように、第三の重りCを、棒の中央の支点に吊り下げても、左右対称であることに変わりないから、釣り合うはずである。ここでアルキメデスは③のように、もとの天秤の左腕の中点と短い棒で作った子天秤の支点とを紐でつなぎ、子天秤の両端に重りAとCを吊るした状態は②と等価であるとした。AとCを吊り下げた子天秤も対称の理から釣り合うはずだから、子天秤の棒は親天秤の棒と同じく水平である。
次に③において、AとCを同時に、互いの両者の中心点、つまり、小天秤の支点まで近づければ、④となるので、これも釣り合うと考えた。ここで、小天秤の支点を吊るしている紐を無限小まで短くし、親天秤の左腕と子天秤の棒とが一体となれば②と同じになる。④の釣り合いは作用点までの長さの比が1:2の場合の梃子の原理を表している。③から④のように、重さが等しい二つの重りを、両者が吊り下がっている点の中点に向けて移動させてもよいなら、多数の重りの場合にも同様な証明ができる。
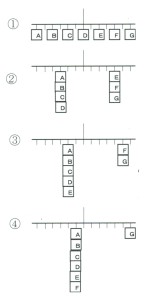
例えば、図5の①のように、支点から左右対称に、同じ重さのA~Gの7個のおもりを等間隔に吊り下げてみよう。これは対称の理から明らかに釣り合う。ここで、BとCを両者の中点に、AとDも両者の中点に移動させ、EとGを両者の中点のFの位置に移動させると、おもりは②のように、A~DのグループとE~Gのグループに分かれ、前者は支点から左に目盛3の位置に、後者は支点から右に目盛4の位置にそれぞれまとまる。①から②の操作は二つの重さの等しいおもりを両者の中点に移動させただけだから①が釣り合うなら②も釣り合うはずであり、腕の長さが3:4の場合の釣り合いが証明できる。同様にして①のおもりをA~Eまでの5個のグループとFとGの2個に分ければ、③のように、前者は支点から左に2目盛のところに寄せ集めることが出来き、後者は支点から右に5目盛のところに集めることができるので、腕の長さが2:5の場合の釣り合いが証明できる。さらに、④のように、重りをA~Fまでの6個のグループとGのみの1個に分ければ、前者は支点から左に1目盛のところに寄せ集め、Gはそのままの位置であるので、腕の長さが1:6の場合の釣り合いが証明できる。
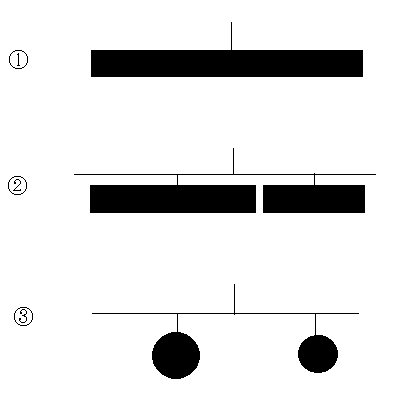
アルキメデスの証明はガリレイらによって受け継がれ、さらに、ラグランジュによって一般化された。ラグランジュの証明を図6に示す。一様な角柱を考え、角柱の中心を支点にして吊るすと、①のように対称の理によって水平につりあう。この角柱を適当なところで二分し、それぞれの中心を糸で吊るすと、②のようにつりあう。これは③と同じである。③では中心から作用点までの距離と重りの重さとが反比例する。
アルキメデス、ガリレイ、ラグランジュと、それぞれの時代を代表する偉大な物理学者の証明は果たして正しいのだろうか?
マッハの批判
エルンスト・マッハはその著書(『マッハ力学―力学の批判的発展史』講談社1969年) のなかで、アルキメデスの証明、およびそれを引き継いだガリレイらの証明を次のように批判している。
「アルキメデスとその後継者の業績を初めて読むと、すばらしいもののように思われるが、厳密に考えてみれば、その正当性が疑わしくなってくる。単に、等距離にある等しい重量は釣り合うという仮定だけから出発して、重りの重さと梃子の柄の長さの反比例が導き出された!こんなことがどうしてできるのだろうか!」
さらに続けてマッハは次のように続ける。
「推論全体が証明すべき法則を暗黙のうちに異なった形で、すでに仮定として含んでいる」
アルキメデスが対称の理から梃子の原理を証明したと称する図4に戻って考えてみよう。図4の③では、両端にAとCを吊るしている子天秤では対称の理が成り立つが、親天秤では対称の理を用いることはできない。つまり、③での親天秤は天秤ではなく、すでに梃子になっている。①と②では天秤の腕である長い棒が水平を保つことは対称の理によって保障されるが、③ではそれが保障されない。梃子の腕が水平から傾けば、子天秤の短い棒と接触する。実際には二つの棒は水平になるので、接触することなく、①から④に移行させるのは可能だが、それは③において、すでに梃子の原理が成り立つているからである。
アルキメデスの証明は、図4の④によって梃子の原理が成り立つことを実験的に示したに過ぎない。図4の①から④に至る一連の操作によって、対称の理から梃子の原理を導いたことにはならない。図5の証明も図6の証明も同様である。
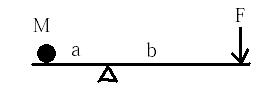
梃子の原理を導いてみよう。図7のように梃子を用いて質量Mの物体を持ち上げる場合、力Fを加え梃子が微小角θだけ傾くと梃子にした仕事はFbsinθであり、質量Mの重りが持ち上げられる高さはa sinθであるから、位置エネルギーの増加はMga sinθである。加えた仕事とエネルギーの増し高はエネルギーの保存則から等しくなければならない。よつて、F=Mga/bとなり、梃子の原理が導かれる。
梃子の原理は、エネルギー保存則から、簡単に証明できるが、アルキメデスから、2000年の時を経て、女性数学者であり、理論物理学者であるエミー・ネーターは、力学におけるあらゆる保存則は、それぞれ、ある種の対称の理から導かれることを証明した。エネルギーの保存則も、時間の並進対称の理から導かれる。梃子や竿秤において、仕事とは無関係に成り立つ釣り合いの法則を、天秤と同じく左右対称の理から証明したとするアルキメデスの推論は間違いであったが、アルキメデスが歴史上最高の科学者の一人であることに変わりはない。人の子である限り、紆余曲折しながら発展するする科学の進歩の過程のなかでは誰でも間違えことはあり得る。

コメント