周期運動によって重力場から永続的にエネルギーを取り出すことは不可能である。しかし、敢えて、その可能性を追求した人々がいた。彼らは重力による永久機関を作ろうとしたのである。その試みは、現在から見れば、「愚行の極み」であるが、力学の教材としては面白い。重力を用いた「永久機関」の例のいくつかを紹介しよう。
ステヴィンの鎖
重力場に置かれた図のような装置を考えてみよう。鎖と斜面の摩擦が充分小さければ、鎖の輪は左周りに回転するだろうか。鎖の輪が架けられている三角形の左右の斜面では左側が右より急斜面だが、回転はしない。
 鎖の個々の玉に働く重力の斜面方向の成分は確かに左側が大きい。しかし、玉の数は右側の斜面上が多いので、鎖全体に働く力の斜面方向の成分は左右の斜面で等しくなり、回転はしない。鎖を三角形の斜面の周りを一周させたとき、鎖の個々の球に働く重力のする仕事はゼロとなるからである。
鎖の個々の玉に働く重力の斜面方向の成分は確かに左側が大きい。しかし、玉の数は右側の斜面上が多いので、鎖全体に働く力の斜面方向の成分は左右の斜面で等しくなり、回転はしない。鎖を三角形の斜面の周りを一周させたとき、鎖の個々の球に働く重力のする仕事はゼロとなるからである。
但し、このステヴィンの鎖と呼ばれる装置を提案したオランダの物理学者ステヴィンは、永久機関を作ろうとしたのではなく、この装置が回転するはずがないと考え、それから力のつりあいの法則を発見したのである。
毛管現象
水の入った水槽に両端が開いたガラス管を差し込み、ガラスと水面との接触部をよく観察すると、ガラス管の内外を問わず、接触部付近の水が水槽の水平面から僅かに上に引き上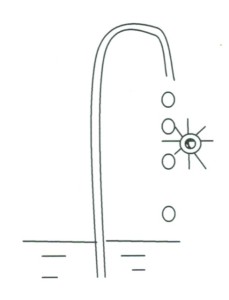 げられていることが分かる。
げられていることが分かる。
これはガラスの付着力と水の表面張力のためである。ガラス管の内径を小さくしていくと、管内の水面は外の水槽の水面よりも高くなる。これを毛管現象、あるいは毛細管現象と呼ぶ。この場合、ガラス管内の水柱の高さは、管内の水を上に引き上げようとする力と水柱の重さとの釣り合いによって決まる。前者はガラスと水面の接触部の長さ、つまり、管の円周に比例し、後者は、水柱の断面積と高さの積に比例するので、ガラス管内の水柱の高さはガラス管の内半径に反比例することになる。
それでは、毛管現象を用いて、「永久機関」が作れないだろうか。毛管現象によってガラス管を登った水が水滴となって落ちるのを利用すれば、羽根車が回転するように思える。しかし、毛管現象はガラスと水との付着力と表面張力によって起こるので、下に曲げられたガラス管の口から水滴が落下することはない。毛管現象を用いて水を高く上げることはできても、それから力学的エネルギーを取り出すことはできないのである。
浮力を用いた永久機関
次に浮力を利用した巧妙な「永久機関」を紹介しよう。水平な中心軸のまわりに回転できる円盤が右半分だけ水中に浸かったような装置を考えよう。円盤には右半分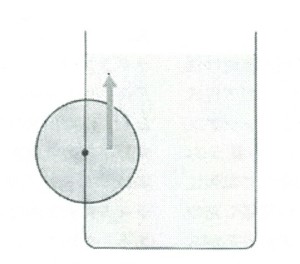 のみに浮力が働くので、左回りに回転するだろうか。
のみに浮力が働くので、左回りに回転するだろうか。
実際にこのような装置を作るのは技術的にきわめて困難であろう。円盤と容器の隙間から水が漏らないようにすると、両者の間の摩擦が大きくなるからである。しかし、この装置が回らないのは摩擦のためだけではない。技術的な問題が解決し、水漏れも摩擦もない装置が作れたとしても、図の円盤は回転しない。それはなぜか? これを考える前に、中学で習った浮力について、一度、復習しておこう。
アルキメデスの原理によれば、液体中の物体には、物体が押しのけた液体の重さに等しい浮力が生じる。浮力とは、物体に周りの液体から働く静水圧の合力であるが、静水圧は、水深が深いほど大きく、物体の表面に垂直に働くので、それらの合力として上向きの力が生じ、それが液体中の物体に働く浮力となる。
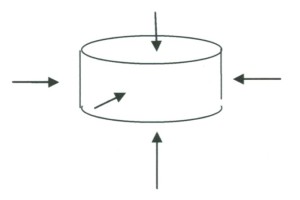 図4のような底面積がA、高さがhの円柱が密度ρの液体の中に存在している場合を考えてみよう。円柱の側面に働く水圧は互いに打ち消しあうが、両底面に働く圧力は下底面のほうが、ρghだけ、上底面に働く圧力よりも大きい。それで、下底面に働く力は上底面の力よりρghAだけ大きくなる。これは円柱が押しのけた液体の重さにほかならない。
図4のような底面積がA、高さがhの円柱が密度ρの液体の中に存在している場合を考えてみよう。円柱の側面に働く水圧は互いに打ち消しあうが、両底面に働く圧力は下底面のほうが、ρghだけ、上底面に働く圧力よりも大きい。それで、下底面に働く力は上底面の力よりρghAだけ大きくなる。これは円柱が押しのけた液体の重さにほかならない。
次に任意の形状の物体に働く浮力についてもアルキメデスの原理が成り立つことを示そう。この場合も、浮力は物体に働く静水圧の合力であるから、浮力は物体の形状や大きさには依存しても、物体の材質にはよらない筈である。物体の形状さえ同じならば、物体が鉄でできていようと、石でできていようと、木でできていようと、物体が受ける浮力は同じ筈である。
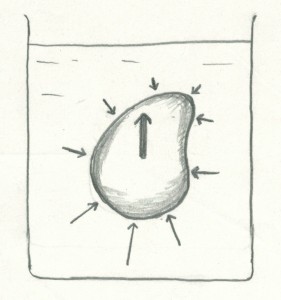 物体が周りの液体と同じ密度の材質でできていたらどうであろうか。いっそ、物体を周りの液体そのものと考えてもよかろう。その場合には、物体は液体中で釣り合って動かないはずであるから、浮力は、密度が水と等しい物体に働いている重力に等しい。つまり、どんな材質の物体も、液体中でのその浮力は物体を液体で置き換えたときの、その液体の重さに等しいことになり、アルキメデスの原理が成り立つことがわかる。
物体が周りの液体と同じ密度の材質でできていたらどうであろうか。いっそ、物体を周りの液体そのものと考えてもよかろう。その場合には、物体は液体中で釣り合って動かないはずであるから、浮力は、密度が水と等しい物体に働いている重力に等しい。つまり、どんな材質の物体も、液体中でのその浮力は物体を液体で置き換えたときの、その液体の重さに等しいことになり、アルキメデスの原理が成り立つことがわかる。
アルキメデスは古代ギリシャの数学者であり、物理学者である。彼はヒエロン王から王冠の金の純度を測るように命じられたとき、風呂から溢れた水の量が体積に等しいことから、王冠の密度の測定方法を考えつき、「Eureka(ユーレカ)!」と叫びながら、王冠を掲げて風呂から裸のまま大通りにとび出したと伝えられている。ギリシャ語で発見したという意味の「ユーレカ」は、発見的なという意味の語、heuristicの語源になっている。
右半分のみが水中に浸かっている円板の話に戻ると、円盤の右半分に働く水圧はどこも円盤の中心に向かって働くから、その合力である浮力も円盤の中心を通り、左斜め上方を向くことになる。そのため、この場合の浮力は回転軸のまわりの、力のモーメントには寄与せず円盤は廻らない。円盤の右半分に働く浮力を、図のように真上の向きに書いたのがそもそもの間違いだったのである。
回転体が楕円板なら?
それでは回転体の形状が円盤でなく楕円の場合ならどうなるだろうか。この場合には装置の製作はさらに難しくなるが、図のようにバネを用いて水漏れのない装置を作ることができたとしよう。今度の場合、回転体の各点に働く水圧は、回転体が円盤ではないので、回転の中心を通らず、回転中心に関する力のモーメントに寄与する。そのモーメントは明らかに、左図aの場合には楕円体を右回りに回転させようとし、右図bでは左まわりに回転させようとするが、aとbとの間のどこかの状態で楕円体は釣り合うことになる。
しかし、回転モーメントが釣り合う場所が存在することだけでは装置が永久機関でないことの証明にはならない。永久機関でないことを証明するには、装置を仮想的に一回転させた場合、回転モーメントのする仕事がゼロになることを証明しなければならない。この場合、回転体はバネからも力を受けているが、一回転した後、バネはもとの状態に戻り、その間にバネがする仕事はゼロであるので、バネから働く力は考えなくてもよい。
回転体が楕円でなく、任意の形状の場合は、回転に伴い水位も変化するので、水圧が変化することも考慮しなければならないのでさらに難しくなる。しかし、浮力は水に働く重力によって生じる。回転体が一回転したあとは、保存場である重力場のなかで、回転体も水位ももとに戻っているので、具体的に計算しなくても重力場がした仕事がゼロであることから廻らないことは明白であろう。
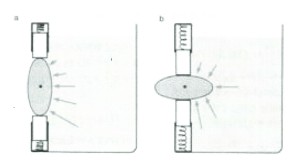 回転体が円でない場合 水圧による回転力が現れ、左図の状態からは右まわりに回転し、右図の状態であれば左まわりに回転するので、どこかで力のモーメントが釣り合う角度が存在する。これで回転しないことを完全に証明したことにはならないが、重力場の中で、装置の状態を一周させてもとに戻っても、重力場は仕事をしないので、回り続けることはない。
回転体が円でない場合 水圧による回転力が現れ、左図の状態からは右まわりに回転し、右図の状態であれば左まわりに回転するので、どこかで力のモーメントが釣り合う角度が存在する。これで回転しないことを完全に証明したことにはならないが、重力場の中で、装置の状態を一周させてもとに戻っても、重力場は仕事をしないので、回り続けることはない。
以上、いくつかの「永久機関らしき装置」を紹介したが、他に電磁気学的な力を取り入れた永久機関も成功した例はない。上に紹介した永久機関のように無からエネルギーを生み出す機関を第一種の永久機関とよぶ。
第一種の永久機関はエネルギー保存則に反するが、これに対して、エネルギー保存則には反せず、しかし、熱力学の第二法則、すなわち、エントロピーの増大則に反する永久機関を第二種の永久機関とよぶ。第二種の永久機関については、いずれ述べることにするが、現在の物理学が正しい限り、第一種であれ第二種であれ、永久機関なるものは存在しない。自然界のしくみは、永久機関の存在を許さないように創られているようである。

コメント
始めまして 80歳の老人です。
錘を使った創エネを考え続けていますが、「加速錘利用の回転装置」を考案してブログに書きました。
重力を使い、さらに加速力をうまく使えば回転し続ける円板が出来ると思います。
錘の円板軸までの水平距離を軸の左右で変化させ、その差を持続させる方法を考えました。
例えば永久機関としてよく登場する「かまぼこ形ループ軌道にオモリを転がす」ですが、あれが回転しないのは軌道の長径が円板の放射線に平行だからで、これを90°ほど回転方向に傾けるだけで解決します。
ただし条件があります。ループ軌道をたくさん(36個くらい)円板に取り付けることと、ループ軌道の長径を出来るだけ長くすることが絶対条件です(=大規模設計)。
設置と同時に始動するし、回転し続けるうえ仕事もするが永久機関ではでありません。なぜなら、重力というエネルギーを投入し続けるから。
以上、ご検討いただきたいと思います。
中澤様、コメント有難うございます。ブログも拝見いたしましたが、結論から言えば、この回転装置が回り続けることはないと思います。確かに、装置の中の重りには、重力が働いていますので、最初は少し回転することがあっても、すぐに釣り合いの状態になり、それ以上動くことはないと考えられます。
重力のエネルギーを投入しているから、従来の、俗にいう「永久機関」ではないとのことですが、装置に外部からエネルギーが入り込む余地はありません。水力発電を「永久機関」と呼ばないのは、水の運動エネルギーとして、外部からエネルギーを取り入れているからです。その元は、ダムの水の位置エネルギーです。さらに、その元を遡れば、太陽エネルギーということになります。しかし、ブログに書かれている回転装置の重りは重力を受けますが、重力のエネルギーを外部から取り入れてはいませんので、もし、これが回転し続けるとすれば、エネルギー保存則が破れることになり、ニュートン以来の力学は完全に否定されることになります。
昔から「永久機関」と称する巧妙な仕組みが考案され、それを見破るのが難しいのも多々ありますが、第一種の永久機関であれ、第二種の永久機関であれ、これまで「永久機関」が、動き続けた試しはありません。無からエネルギーを生み出す永久機関を作ろうという試みは、二十年程前に科学界で大騒ぎになった常温核融合への挑戦よりも遥かに無謀なことだと思います。
nobuyuki さま
コメントありがとうございました。
nobuyuki さま
コメントありがとうございました。しかし納得がいきません。
ループ軌道の長径が充分に長く、しかもそれが36個もあれば回転が始まるわけですね。
この回転が10°進めば元の状態になるわけで、回転が継続することになるでしょう。
仮に10°進まないなら、ループを72個にすれば5°進めば元の状態になるわけで、これなら回転が継続することになるでしょう。
この装置の絶対条件としてあげたことを充分に考慮していただきたいものです。
あなた様は「装置の中の重りには、重力が働いていますので、最初は少し回転することがあっても」としながら、それがエネルギーではないとおっしゃる。「すぐに釣り合いの状態になり」といわれる根拠が知りたいです。
中澤
中澤 様
地球上ですから、当然すべての物体に重力が働いています。床の上に静止している物体には重力が働いても、重力が仕事をしないのは当然ですが、動いていても、重力場の中で閉じた曲線上を運動する物体に対しても仕事はしません。例えばジェットコースターを考えて下さい。その軌道が円であり、コースターにはモーターもエンジンもないとすると、コースターは重力を受けて、高い所では速度は遅く、低くなると早くなりますが、重力が仕事をしてコースターが回る速さがどんどん加速されていくことはありません。これは軌道が円軌道でなくても、閉じた軌道であれば、同じく加速されることはありません。また複数個が動いていても、全体の運動エネルギーが増すことはありません。重力が仕事をするのは、物の落下運動のように、上から下への一方向の運動をする場合です。その場合は、落下物は重力のする仕事のため、落下するにつれ、運動エネルギーを増していきます。
考案された回転装置も、軌道の長径が長くても短くても、また重りの数を増やしても減らしても、残念ながら、そこからエネルギーを取り出すことはできません。それは重力場が保存場だからです。保存場と非保存場の違いについては、私のこのホームページの「メダカの学校は川の中」を読んでいただければと思います。
また、これまでの永久機関の歴史については、「永久運動の夢」をいう本が出版されていますので、これを参考にされることをお勧めいたします。
nobuyuki さま
返信をためらいますね。ここまで世間知らずとして扱われては返す言葉もないけど、発明の根幹だけでも記します。
発明の基幹は、ループ軌道の長径を回転方向に90°ほど傾けることにあります。
これによって錘の動きが90°早まって、有効成分が水平軸に集まる。即ち、錘が最外輪に達するときの角度が軸に対して水平近傍になり、回転モーメントに関わる距離がcos0°の責なので、水平距離そのものが回転モーメントに関わります。
さらに、最下端にある錘が軸側に戻るにあたり、下端近辺はcos90°近辺であって数値はゼロに近く、逆回転モーメントが激減します。
以上の2点が相乗効果として現れます。
言い換えると、同じ錘を繰り返し使えるようにした措置であって、軌道が傾かないダ・ビンチのかまぼこ型永久装置では絶対に得られない効果です。
しかしあなたは、多くの人がのたまうありふれた理屈を述べるにとどめ、私の基幹発想についての記述がないのが不満です。
科学の教条を盲信するもよいけど、もう少し探求の目でみてほしいです。
nobuyuki様
私を無視されたようですね。
この装置は設置と同時に始動し、回転し続けます。これがあなたに認められ、学際側の認知を得ることを期待しましたが無駄だったようです。
あなたは私の装置を永久機関とされました。しかし、いわゆる永久機関ではありません。なぜなら、水力発電と同じく位置エネルギーを利用するからです。
あなたは、水力発電は「水の運動エネルギーとして、外部からエネルギーを取り込んでいる」とされるけど、つまりは「水の位置エネルギーを運動エネルギーとして利用している」わけです。
さらにあなたは、「装置に外部からエネルギーが入り込む余地はない」とおっしゃるが、内部のすべての錘にもそれぞれに位置エネルギーはあり、円板軸の左右差を演出できるのです。私の演出は、軌道の長径を進行方向に90°ほど傾けることです。実際に回転します。
私はたくさんの実験を繰り返してここまでたどり着きましたが、軌道の形状と長径の角度がうまくいったときには回転し続けます。ただ軌道数が6個の小規模なため、発電などの仕事をする「実機」の制作ができていないだけです。
さて、永久機関でないことを念頭において、私の図面を目にすると、誰もが「回るかも」と言います。HPで示した軌道が36個の画像は静止状態だが、円板の右が重いのがわかります。静止状態からでも動き出す力があることになります。これはあなたも否定できないはずです。
そこで、これが10度だけ回転して静止したら、まったく同じ状態になります。この10°動くまでの中間の錘の動向は僅かで、逆転なんてあり得ません。ということは10°進むことができれば回転し続けることになります。HPでは軸より50㎝のところで172グラムの力があることを示しました。この値は10°回転させるに充分です。
昨年のことですが、試作会社に試作を打診したことがあります。その返答はこうです。
「この手の依頼はお断りしていますが、いろいろ検討されておられることがわかりました。考え直してみると、私どもが廻る廻らないを云々するのは僭越で、おかしいような気がしてきました。試作しましょう」
この申し出に対して、私は、費用の工面ができずにそのままにしております。
装置は、摩擦とかバランスの不均衡といった負の要素があっても回転します。あなたの論理とは真逆です。
大変お手数をおかけしました。おつきあいをいただいて有り難うございました。
中澤