1.バネ付き振り子
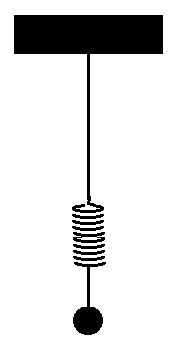
図1ように、バネと重りと糸からなる振り子を天井から吊り下げ、糸の長さを適当に調節し、振り子に上下振動を与えると、上下振動は安定ではなくなり、横揺れ振動が現れ、重りは上下振動と横振動とが混じった∞字形の軌跡を描き、次に横揺れ振動のみになり、それも不安定になり、∞字型の振動が現れ、再び縦揺れ振動になり、それを繰り返す。つまり、縦揺れと横揺れとが交互に現れる連成振動になる。
バネ付き振り子の運動を運動方程式を極座標表示すると、非線形の連立方程式になり、解析的には解けない。計算ソフトを用いて、解くしかないが、バネ付き振り子の運動をどう説明するか、まず、線形の通常の連成振動について考えてみよう。
2.線形連成振動
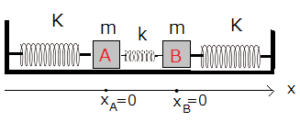
図2のような二つの重りと三つのバネからなる系の連成振動について考えてみよう。図のつり合いの状態から二つの物体AとBが、それぞれ、xA,xB変位したとすれば、その瞬間、左端のバネはxA伸び、真ん中のバネはxB-xAだけ伸び、右端のバネはxBだけ縮んでいる。よつて、物体A、Bの運動は次のような線形方程式で表すことができる。
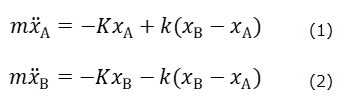
(1)+(2) および、(2)-(1)より、
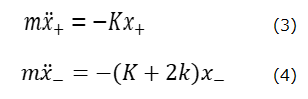
ここで、x+=xA+xB、x–=xB-xAとする。(3)と(4)で表される単振動が図1の系の固有振動であり、系の振動は二つの固有振動の線形結合として表される。(3)は重りAとBとが一定の距離を保ちながら振動するときの運動方程式であり、このとき中央のバネは伸び縮みしないので、その振動数はkに依存しない。一方、(4)は系の重心は変わらず、AB間の距離が振動する運動であり、どのバネも伸び縮みするので振動数はKとkの両方に依存する。ここで簡単のため、二つの角振動数をωとεを用いて
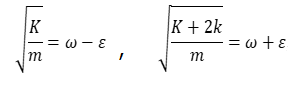
とすると、二つの固有振動(3)(4)は次のよう表せる。
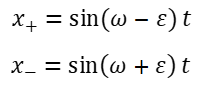
一般に、系の運動は上記二つの固有振動の重ね合わせとして表される。例えば、t=0での初期条件として、xA(0)=0,xB(0)=1ときのAとBの振動は、振動数の僅かに異なる固有振動の差または和の半分として表されるので、それぞれ、次のようなうなり振動になり、AとB間でエネルギーが周期的に交換するる。
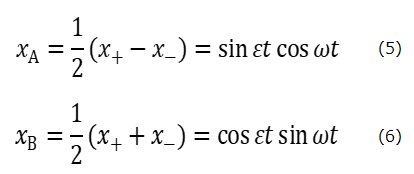
K>>kとすると、ε<<ωであるから、(5)と(6)は、それぞれ、sinεtおよび、cosεtで振幅変調された振動であり、xAの振幅が0のとき、xBの振幅は最大になり、xAの振幅が最大のとき、xBの振幅が0になることを示している。さらに振幅が0となる前後で振幅の符号がかわるので、その瞬間、図3(物理教育学会誌表紙より)に示すように、振動の位相が反転する。
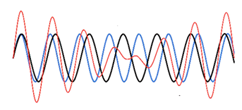
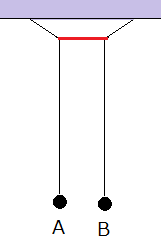
図2の系と同じ連成振動は、図4のように長さの等しい二つの振り子AとBからなる連成振り子でも実現できる。静止している状態から一方だけを振らせると、他方はは位相が90°遅れて振れだす。位相が先行する振り子ははエネルギーを奪われ減衰し、遅れているほうはエネルギーを得て、その振幅が増大する。他方にエネルギーを与えて振幅が0になった瞬間、その位相が180°反転する。そのため、二つの振り子の位相差が逆転し、今度は、エネルギーを得て増幅し始める。これを繰り返しながら、力学的エネルギーが二つの振り子AとBの間で交互に移動する。
次にAとBとを前後に同位相で振らせる場合、逆位相で振らせると場合とが図4の系の固有振動であり、二つの固有振動は僅かに振動数が異なるが、どちらも安定な振動になる。図4を図2と比較すれば、どちらも線形の連成振動であり、同位相の振動がx+振動、逆位相の振動がx–振動に相当する。図2と図4の線形の連成振動を参考にしながら、図1のバネ付き振り子の運動について考えてみよう。
3.バネ付き振り子の連成振動
バネ付き振り子の運動を詳細に観察すると、次の図5のような変化をしていることが分かる。
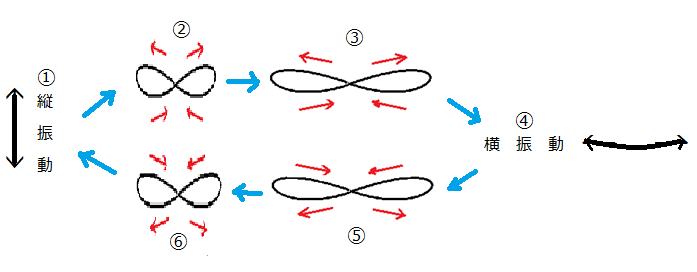
縦振動①から始まった重りの運動の軌跡は②から③への変化のように、∞字運動の縦幅を狭め横幅を広げながら④になる。④になって縦振動が0になった瞬間、縦振動の位相が反転し、次は⑤から⑥への変化のように縦幅が広がり横幅を狭めながら縦振動に戻る。その瞬間、横振動の位相が反転し、再び②や③へと変化する。バネ付き振り子の重りは糸の長さを適当に調節すると図6のAとBのような二つの∞の字形の運動をする。
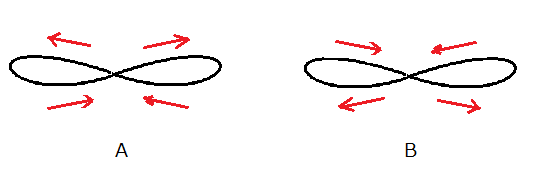
図5の①から④の過程ではAの運動をし、④から①への過程ではB運動である。④においてAからBへの転換が起こり①でBからAへの転換が起きている。①と④とで、横振動および縦振動の位相が反転し、それぞれBからAおよびAからBへと運動の向きが変化する。
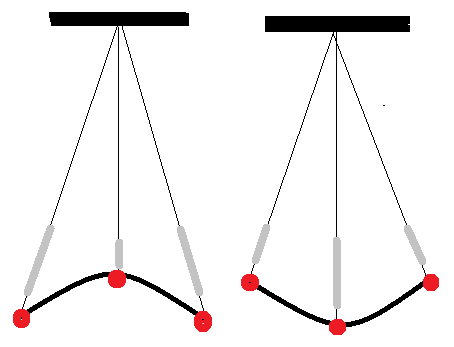
それではバネ付き運動でも固有振動が存在するだろうか。図7の左図のようにおもりを斜め下に引っ張り手を手を放すと上に凸の運動を繰り返す。また、右図のように斜め上に上げて落とすと下に凸の運動をする。この二つの振動がバネ付き振動の固有振動のように見えるが、長続きしない。図2や図4の運動が線形運動であり、重ね合わせの原理が成り立ち、安定な固有振動が存在するのに対し、バネ付き振り子は非線形振動であるため、重ね合わせの原理は成り立たない。不安定な図7の振動は準固有振動と呼ぶべきであろう。
4. ブランコの運動
バネ付き振り子も通常の連成振動も空気の抵抗などがなければ、系全体のエネルギーの和は一定である。つまり、物体の運動エネルギー、重力の位置エネルギー、バネのエネルギーなどの全てのエネルギーの和が一定の系である。しかし、図8のようにブランコでは動力源が系内に存在し、また、ボタフメイロ(スペインの教会の振り子)では系外の動力源からエネルギーが系内の補給されている。
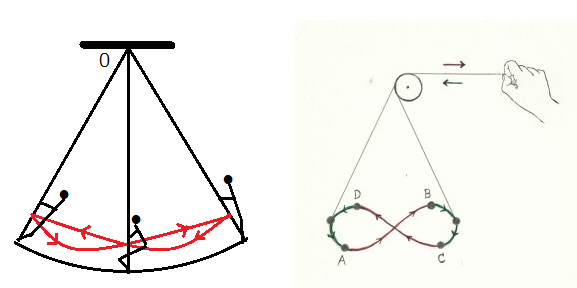
バネ付き振り子では、バネのエネルギーが無くなると、横揺れは増幅から減衰運動に変化するが、ブランコやボタフメイロでは、内部や外部の動力源から上下運動のエネルギーが補給されている。ブランコもボタフメイロも横揺れを増すとき、人の重心や重りは図6のAと同じ軌道を描くことによって横揺れが増幅する。
5.バネ付き振り子のシュミレーション

バネ付き振り子のシミュレーションをっするには曲座標系を図9のように選ぶと運動方程式は次の通りになる。あとは数式ソフトに任せればよい。連立方程式の未知数はrとΘとT、糸の長さlを重りが∞字形を描くように実験も数値計算も選んで比較すればよい。

6.蛇足ながら
0から9までのアラビア数字のなかで、0を除けば、8だけが閉曲線であるが、8の字の物理や数学が面白い。バネ付き振り子の運動以外にも、準天頂衛星の軌道、三体問題における、ラグランジュ解以外の安定解、日常生活におけるロープやホースの8の字巻きなど、興味のある方は一部重複するがコチラも→8の字運動の力学
ブランコに乗った子供はその筋力でブランコの上で上下運動をする。ブランコの鎖の張力は上下運動に負の仕事をし、ブランコの横揺れ振動に正の仕事をする。ブランコでの重心の8の字運動、それがバネ付き振動とブランコを繋ぐ重要なキーワードかも知れない。

コメント