最近、物理関係者だけに感染する不思議な病気が蔓延しているという。もともとは、40年前にアメリカから輸入された奇病だが、もし、抗力が仕事をすると聞いて虫唾が走るようなら、真っ先にこの病気への感染を疑ったほうがよい。進行すると、蕁麻疹、円形脱毛症、帯状疱疹と様々な症状が現れ、重篤な場合は死に至ることもあり、放置するのは危険である。しかし、病院に行かなくても簡単に在宅で治せる耳寄りな治療法がある。奇病の原因は、ニュートン力学と、抗力に対する固定観念との間で板挟みになり、そのストレスであることは確かだから、Pseudoworkなどの、「妖怪のする仕事」を仮定した、都市伝説まがいの怪しげな学説に惑わされず、ニュートンの運動法則から、抗力が仕事をしていることが明らかな例を一つだけ示せばよい。例えば、ころがり運動の運動方程式を作り、それから抗力のする仕事を導くことができれば、それだけで完治するはずである。これは治療法としてだけでなく、感染予防にも有効である。詳しくは以下のマニュアルを参考にして頂きたい。数式を追い、それをニュートン力学に照らして確認するのは少々面倒だが、物理関係者、なかでも物理教育関係者は、感染の有無に関わらず、将来物理を志す生徒を感染から守るためにも、ぜひ、この機会に一度試して頂きたい。
重力と抗力の釣り合い
図1のように、水平な台上に半径α、質量Mの円柱を静かに置いたとき、円柱が台から受ける抗力Rは鉛直上向きであり、その作用線は重力Mgの作用線と一致する(ただし、図では分かりやすいように僅かにずらして描いている)。重力と抗力とは互いに逆向きであり、大きさは等しく、両者は釣り合う。
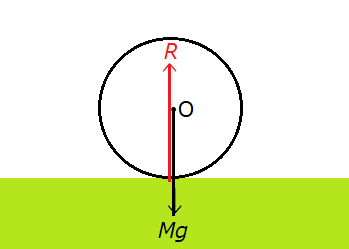
しかし、重力と抗力とが釣り合った図の状態において、水平方向に動力源による第3の力を加えるとつり合いは破れ、円柱はころがり出す。このとき、円柱に働く重力は変わらないが、抗力Rに水平成分Fが現れ、Rの向きは垂直ではなくなる。
円柱が転がるときの抗力
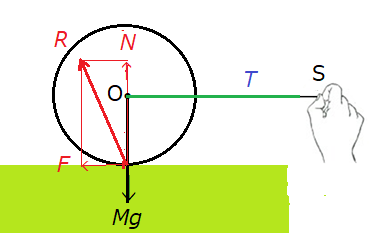
図2のように、円柱の中心軸に質量の無視できる取っ手OSを取り付け、第3の力として、水平右方向に力Tを加えて引っ張ると、円柱と台との摩擦のため、抗力Rに、水平方向左向きの成分Fが現れ、抗力Rの向きは鉛直上向きではなくなり、図のように左斜め上方向に傾く。Rの鉛直方向の成分、つまり、垂直抗力Nは重力とつり合うが、Tと抗力の水平成分Fとによって円柱にころがり運動が生じる。ころがり運動は、並進と回転の二つの運動からなる複合運動であり、円柱の中心軸のまわりの慣性モーメントをI、重心の速度をv、回転の角速度をωとすれば、その運動方程式は、二つの式からなる連立方程式になる。並進運動(重心運動)に対しては質量は全て重心に集中していると考え、力の作用線も重心を通るように平行移動することができるが、回転運動に対してはどちらも許されない。連立運動方程式は次のようになる。
T–F=M×(vの時間微分) (1)
Fα=I×(ωの時間微分) (2)
(1)式は並進運動の運動方程式であり、(2)式の左辺の、Fと半径αとの積Fαは円柱に働く時計まわりの力のモーメント(トルク)である。円柱のころがり運動は並進運動と回転運動とが抗力を通して連動しているので、その運動方程式は、(1)と(2)のように、並進と回転の二つの運動方程式が水平抗力Fによって連結した連立方程式になる。微小時間dtにおける重心の変位dxは、dx=vdtであり、同じくdt時間に回転した角度dφは、dφ=dx/α=vdt/α=ωdtである。(1)の両辺にvdt、(2)の両辺にdφを掛ければ、両式は数学を用いて、それぞれ、
(T–F)dx=d{Mv2/2} (3)
Fdx=d{Iω2/2} (4)
となる。円柱の中心軸のまわりの慣性モーメントをI=kMα2とし、さらに、滑らない条件から、v=αωであるから、(3)式と(4)式の右辺の比は、1:kになる。左辺の比も同じであから、k(T–F)=Fであり、Fの大きさはF=kT/(1+k)となり、Tが与えられれば、Fの値も決まり、その向きは図のように左向きである。ただし、kは、0<k<1の定数であり、質量の分布が中心軸から離れているほど大きくなるが、一様な密度の円柱では、k=1/2であり、I=Mα2/2、そして、図2の場合では、F=T/3となる。
(3)と(4)の左辺は、円柱に働く水平抗力Fは、並進運動に、ーFdxの負の仕事をすると同時に、回転運動に対してはFdxの正の仕事をすることを明確に示している。もし、Fが仕事をしなければ、Tがした仕事によって円柱が得た力学的エネルギーはすべて並進運動のエネルギーになり回転運動に配分されない。抗力のする正と負の仕事によって並進運動と回転運動とに、2:1の比で運動エネルギーが再配分されていることが分かる。
次に図3のように円柱に巻きつけた糸に力Tを加えてころがす場合を考えてみよう。今度は抗力がどちらに傾くかを図から予測するのは難しいが、一旦、抗力は斜め右方向に傾くとして、つまり、抗力の水平成分Fは右方向に向くとして計算してみよう。
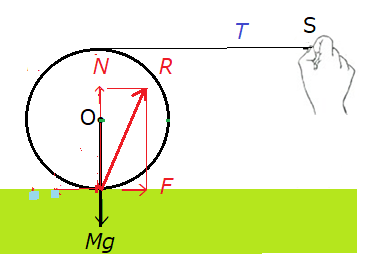
この場合も、抗力の垂直成分Nと重力とが釣り合うのは図2の場合と変わりないが、今度は重心運動および回転運動の運動方程式はそれぞれ、次のようになる。
T+F=M×(vの時間微分) (5)
(T-F)α=I×(ωの時間微分) (6)
よつて、図2の場合の(3)と(4)に相当する式は、図3の場合では、
(T+F)dx=d{Mv2/2} (7)
(T–F)dx=d{Iω2/2} (8)
となるが、今度は、T+F:T–F=2:1から、水平抗力の大きさは、F=T/3となり、その向きは図3で示されるように右向きでよいことになる。図3の場合も、Fが仕事をしなければ、力学的エネルギーは並進運動と回転運動とに同じだけ配分されるが、水平抗力は並進運動に正の仕事をし同時に回転運動に対して負の仕事をすることによって、並進運動と回転運動とに力学的エネルギーが、やはり、2:1の比で再配分される。
力学的エネルギーの保存則
図2の円柱の運動において、(3)式と(4)式とを加えると、抗力のする仕事は消えて、
Tdx=d{Mv2/2+Iω2/2} (9)
となる。一方、図3の運動の場合は、(7)と(8)を加えると、
2Tdx=d{Mv2/2+Iω2/2} (10)
(9)および(10)式は、それぞれ、図2および図3の運動に対する力学的エネルギーの保存則である。図2では力Tの作用点の変位は重心の変位dxに等しいが、図3では力Tの作用点の変位は重心の変位の2倍になる。複合運動全体にする仕事は、力とその作用点の変位との積であり、仕事Bである。作用点の動かない抗力はエネルギーを供給できないので全体運動に対しては仕事をすることはできないが、複合運動の個々の運動に対しては(3)(4)式、または(7)(8)式が示すように抗力も仕事をすることができる。
抗力は仕事をしないとするなら、(3)(4)式や(7)(8)式の連立方程式が否定されることになり、(9)式や(10)式をどのようにして、導くのだろうか。抗力のする仕事を否定しては、複合運動におけるエネルギーの配分が説明できないだけでなく、エネルギー保存則も説明できなくなる。正常な人間なら、抗力の仕事を否定されるほうが蕁麻疹がでよう。
円柱のころがり運動に対し、抗力が仕事をしても、抗力は正と負の仕事を同時にするので、一切、不都合なことは起きないことが分かる。これでもう蕁麻疹も帯状疱疹も出ないはずである。なに!まだ蕁麻疹が? いや、それはただの汗疹、大丈夫。次は自信と勇気をもって、日常経験する複合運動に、抗力のする正負同時一対の仕事を適用してみよう。
自転車の車輪に働く水平抗力
円柱のころがり運動では動力源は外部に存在していたが、動力源が系の内部に存在する場合も、抗力は正と負の仕事を同時にすることによって運動間にエネルギーを配分している。
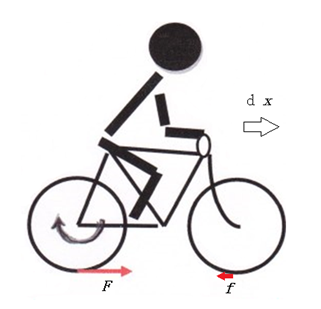
後輪が地面から浮いていれば、摩擦がないので、いくらペダルを踏んでも、後輪が回転するだけで、自転車には進行方向の力が働かないので自転車は走れない。しかし、後輪が地面に接していれば、図4のように地面との摩擦によって、後輪には地面から進行方向に水平抗力Fが働く。Fは後輪の回転とは逆回りのトルクを後輪に及ぼす。つまり、後輪の回転運動に負の仕事をする。それとともに、Fは人も含めた自転車の並進運動に仕事をする。並進運動が生じると前輪にも後ろ向きの僅かな水平抗力fが生じ、fは前輪の回転運動にトルクを及ぼし前輪の回転運動に仕事をするとともに、自転車の並進運動に負の仕事をする。人の足が仕事をして得られた後輪のエネルギーが、抗力Fとfのそれぞれがする正と負の仕事によって、並進運動そして前輪の回転運動へと伝達する。
垂直抗力がする仕事
円柱のころがり運動でも、自転車の運動でも、垂直抗力は重力とつり合い、運動に寄与しなかったが、垂直抗力も、垂直方向の運動が存在すれば仕事をする。その場合にも抗力は、複合運動の一方の運動に正の仕事をしていれば、必ず他方の運動に負の仕事をしている。
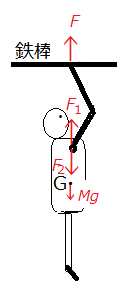
図5のように鉄棒で懸垂する場合、その運動は、重心運動と腕の変形運動からなる複合運動である。 人に働く力は、人の重心に働く重力Mgと手の平が鉄棒から受ける垂直抗力Fだけであるが、Fがどのような役割をしているかを考えるために、腕の付け根に、大きさがFと等しく、向きがそれぞれ上向きと下向きの力F1とF2とが働いているとしても両者は打ち消し合うので運動には関係しない。人には重力以外に、FとF1とF2の三つの力が働いていると考えてもよいことになる。つまり、Fの役割を考える代わりに三つの力の役割を考えればよい。その中の二つの力FとF2は、腕の両端に働き、腕を縮めようとする筋力に逆らって腕を伸ばそうとする。残りの上向きの力F1が腕の付け根に働き、その大きさが重力Mgより大きければ重心を引き上げることができる。三つの力は、腕を縮めようとする変形運動に負の仕事をして重心運動に正の仕事をすることになるが、もともと、重力以外にはFしか存在しないので、変形運動にする負の仕事も、重心運動にする正の仕事も、抗力Fがしていることになる。
ローラースケートを履いた人が手で前方の壁を押すとき、壁を押す力をFとすると、人の手は壁から力F’で押し返される。作用反作用の法則から、FとF’とは大きさが等しく向きは互いに逆向きである。壁は動かないので、壁に働く力Fは壁に仕事をすることはできない。しかし、壁から人に働く力F’は、その作用点は動かないが、人は動くので、F’は動くので人の運動に仕事をすることができる。抗力F’は、人が腕の筋力によって腕を伸ばそうとする変形運動に負仕事をして人の重心運動に正のす仕事をする。
ブランコ
ブランコは人の重心の振り子運動と人の変形運動とがブランコを吊るしている鎖の張力によって連動した複合運動である。鎖の張力は、抗力と同じくその作用点は動かず、束縛力であり、正味の仕事はしないが、人の変形運動に負の仕事をして、重心の振り子運動に正の仕事をしている。この場合も張力は二つの運動に正負同時一対の仕事をすることによって、変形運動のエネルギーを重心の振り子運動に伝えている。詳しくは→ブランコとボタフメイロ
まとめ
- 運動法則は作用点が動くか動かないかで力を区別してはいない
- 運動に制限を加えることができるのは運動法則と初期条件だけである
- 抗力は仕事をしないという制限をさらに加えれば、力学の適用範囲が単一運動のみになる
- 複合運動において抗力が仕事をしてもエネルギー保存則に反しない
- 抗力は、複合運動に対し、正と負の一対の仕事を同時にしている。
関連するページ→ 妖怪に牛耳られた力学教育

コメント