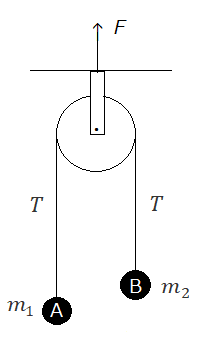
図1は、質量の無視できる滑車と、質量がそれぞれ、m1、m2の二つのおもりAとBを用いたアトウッドの装置である。滑車を通して二つのおもりを繋いでいる糸の張力をT、おもりAおよびBの速度を、それぞれ、v1、 v2とすると、鉛直下方を力の正の方向として、二つのおもりの運動は、(1)~(3)式からなる次の連立方程式で表される。
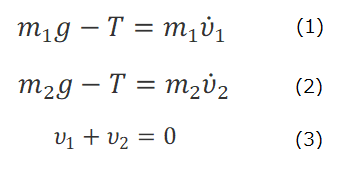
ここで、未知数は、T、v1、 v2 の三つであり、式の数も3であるから、あとは数学を用いて好きなように解けばよい。結果は
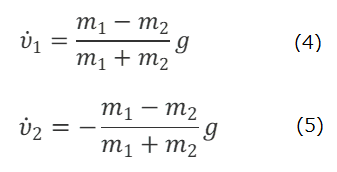
となり、おもりAとBは互いに逆向きに大きさが同じ等加速度運動をすることが分かる。あとは初期条件のもとに、(4)式または(5)式から、質点の速度や位置を求めるだけでよく、糸の張力Tの値とは無関係に問題は解ける。
しかし、敢えて、張力Tはこの運動にどのような役割をしているについて、考えてみよう。AとBからなる2質点系の質量をm、質点系の重心の速度をvGとすると、m=m1+m2、mvG=m1v1+m2v2であり、(1)式と(2)式を加え合わせると、

となり、(6)式は2質点系の重心運動に対する運動方程式である。重心も等加速度で落下運動するから、Tは一定であり、(6)の両辺にvGdtを掛けると、
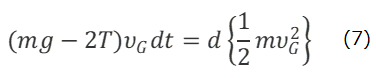
となり、滑車の質量はないものとしているので、2Tはアトウッドの装置が天井から上向きに受ける抗力Fに等しい。(7)式は、重力mgが2質点系の重心の落下運動に正の仕事をするのに対し、抗力2T、つまり、Fは2質点系の重心の落下運動に負の仕事をしてることを示している。
しかし、Fはもう一つの仕事をしている。それを示すために、(1)式の両辺に、v1dt、(2)の両辺にv2dtを掛ければ、それぞれ、

となる。(8)と(9)式を加えて、さらに(3)式を用いれば、
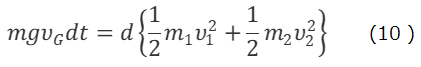
となる。(10)式は重力がした仕事の分だけ、系の運動エネルギーが増えたことを示し、エネルギーの保存則である。(7)式と(10)式から、抗力Fのする仕事は
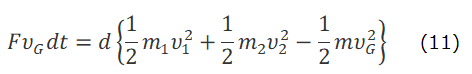
となる。ここで、v1=vG+v‘1、 v2=vG+v‘2とすると、(11)式は
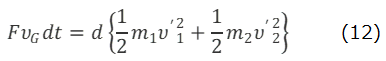
となり、右辺は重心系から見た二つの質点の運動エネルギーだから、2質点系の変形の運動エネルギーである。(12)式は抗力Fがした仕事が系の変形運動のエネルギーの増し分になることを示している。。抗力Fは(7)式で表されるように並進運動に負の仕事をし、(12)式示されるようにその分だけ変形運動に正の仕事をしていることになる。
アトウッドの問題を解くだけなら、抗力Fのする仕事などを考える必要はないが、敢えて抗力が仕事をすると考えても、(6)式~(12)式に示されるように、矛盾は一切生じない。しかし、系内にエネルギーを供給する動力源が含まれる場合は抗力のする仕事を考える必要がある。
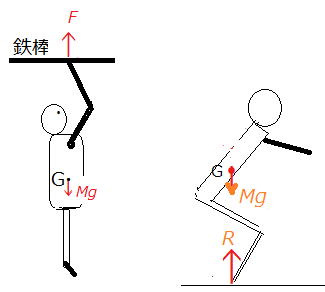
図2のように、懸垂やスクワットで、人の重心が上がる場合、その運動方程式は、重心運動に対する運動方程式と変形運動に対する運動方程式からなる連立方程式になるが、重心運動に対しては数式化できるが、変形運動に対しては数式化できない。しかし、FやRの抗力が変形運動に負の仕事をして重心運動に正の仕事をすると考えれば矛盾は生じない。詳しくは、迷路からの脱出:抗力と仕事 を参照して頂きたい。
懸垂もスクワットもエネルギーを供給したのは動力源の筋力だが、そのエネルギーがどのようにして重心運動のエネルギーに伝わるかを説明するには抗力のする同時一対の仕事が必要である。変形運動のエネルギーも重心運動のエネルギーも、その出所は筋力であることに違いないが、会計報告書に譬えれば、筋力が仕事をしたというだけで、筋力の仕事で得た収入がどのように使われたのか、その支出の内訳を示さなければドンブリ勘定の会計報告書になる。日本物理教育学会はドンブリ勘定の力学を推奨するのだろうか。
物理教育に誤概念が多いのは事実である。それを正すことは、物理教育の重要な役目の一つであるが、この問題に関する限り、物理教育学会自体がアメリカ発の誤概念を信じ込み、ニュートン力学との狭間で身動きできない状態に陥っているのではないだろうか。古典力学はニュートンファーストであり、アメリカファーストではない。都市伝説まがいのpseudoworkを信じ込み、ミイラ取りがミイラになってはならない。

コメント