身体検査の日の思い出

　どんな検査かは知らないが、最近は大臣候補も身体検査を受けるという。身長や体重の測定ではなさそうだし、また、認知症などの検査なら、本当に検査をしたのかと疑いたくなるような国会答弁もあるが、昔、小学校で定期的に行われていた健康診断も身体検査と呼ばれていた。

「ほら、そんなに動いたら、測れんではないか！」身体検査の日、体重計に乗ったやんちゃ坊主が先生に注意されていた。アナログの頑丈な体重計で測定していた戦後まもない頃の話である。

　体重計の上で動いたら、体重が変わるのだろうか。変わらないなら、なぜ体重計の針は振れるのか。その日の疑問は、中学生になっても分からず、高校の物理で加速度を習い数学で微分を習って初めて理解できた。

　その後、物理学の道に進み、やっとの思いで長崎大学の教養部に職を得たものの、安穏の日々は長くは続かず、やがて教養部が廃止され、教養部難民の憂き目を見ることになった。結局、新しくできた文理融合の学部に残ることになったが、その環境科学部で、修士課程の入試問題作成を担当したとき、昔を思い出し、次のような体重計の問題を出題した。

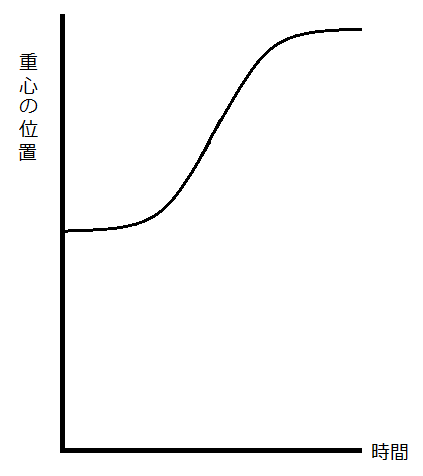
　体重計の上で屈んだ状態から、立ち上がるとき、人の重心の高さが図１のような変化をしたとする。体重計の針の質量は無視できるとすると、体重計の針はどのような振れ方をするか。

　既に物理も数学も高校で習い、さらに大学でも習っているはずであり、全員正解かと思ったが、意外にも正確に答えた受験生はいなかった。

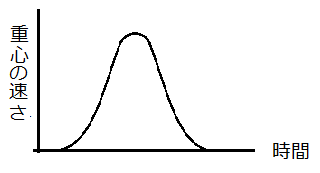
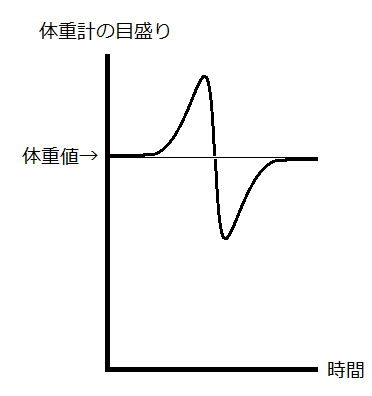
　体重計の針が指す目盛りの値は足の裏が体重計を押さえつける力であり、その力の大きさは作用反作用の法則から体重計が人の足の裏に及ぼす上向きの力Rに等しい。人の質量をMとし、人の重心の上向きの加速度をαとすると、人の重心の運動方程式は、R－Mg＝Mα となり、R、即ち体重計の針が指す目盛りの値は、MgとMαとの和になる。前者は一定であるが、加速度αは、図１で表される重心の高さを時間で2回微分して得られる。つまり、重心の位置を1回微分すると、重心速度は図２のようになり、それをもう１回微分すると加速度が得られ、体重計の針は図３のような変化をする。人が極めてゆっくりと立ち上がるとき、つまり、準静的に立ち上がれば、速度は常に0、加速度も０であるから、そのとき針はほとんど振れない。

　大学院受験者に、この問題の正解者がいなかったのは在職時の衝撃であったが、もっと衝撃的なことを定年退職後に体験した。いや、今も継続中である。人に働く上向きの外力は体重計から受ける抗力Rだけであるのに、Rには重心運動の加速度の変化が反映されているのに、Rは作用点が動かないので一切運動に仕事をしないとは?

　さらに、高校教科書の仕事は初心者向けの定義だとは？　力学に都市伝説のような得体の知れない仕事が存在しているとは？　しかも、いつの間にか力学では、それが定説になっているとは？　しかし、高校でも大学でもそう習った記憶が全くない！　また、学生にそんなことを教えた記憶も一切ない！　ここ数年、驚天動地、物理教育に何が起きたのか、狐につままれたような気分である。さては認知症のはじまり？　来るべき時がついに来たのだろうか。確かに最近物忘れがひどくなったが、政治家ならいざ知らず、認知症には少々まだ早いような気がするのだが。　

関連するページ　：どうする物理教育！