図1のように、人が台車の上に仰向けに寝て、足で壁を押せば、人と台車からなる系の重心は、右に動き、系の重心運動に力学的エネルギーが生じる。系の重心運動に仕事をした力は壁から受ける抗力Fか、それとも、腰の関節が足の付け根から受けるFSだろうか。
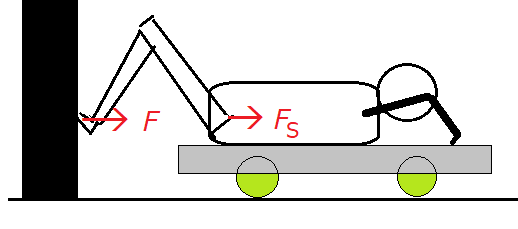
Fの作用点は壁だから動くことはないが、FSの作用点は腰の関節だから右方向に動く。系の重心運動に仕事をするのは作用点の動くFSだと考えたくなるが、FSが仕事をするのは、足を除いた胴体と台車の重心運動に対してである。足にも質量があるので、FSはFより小さくなる。一方、足まで含めた系に働く外力はFだけだが、作用点が動かないので、Fは系に力学的エネルギーを供給することはできない。
エネルギーを創出し、それを系の変形運動に供給しているのは、足を延ばすために仕事をする腰や膝の筋肉の力だが、そのエネルギーが系の重心運動に供給されるためにはFのする仕事が重要である。人と台車からなる系の質量をM、重心の加速度をα、速度をvとすると、重心運動に対するニュートンの運動方程式は次の1式で与えられ、その両辺に重心速度vを掛け、時間tで積分すれば、系の重心の運動エネルギー、EGは、数学を用いて2式のように表される。
- F=Mα
- EG=∫Fvdt=M∫αvdt=Mv2/2
運動方程式から考えれば、壁から受ける抗力が仕事をすると考えても何も問題がないようにように思えるが、約40年前に、アメリカで発表された論文、Pseudowork and real work (Am.J.Phys.51(7),July1983)によれば、Fは作用点が動かないので、2式は仕事に似て仕事でない Pseudowork であり、Fが仕事をすると考えてはならないという(Pseudowork説)。それ以来、抗力は一切仕事をしないとする考えが学会の主流となっているようだが、2式は系に供給されたエネルギーではなく、系の重心運動に供給されたエネルギーである。さらに、vはFの作用点の速度ではなく、系の重心の速度である。
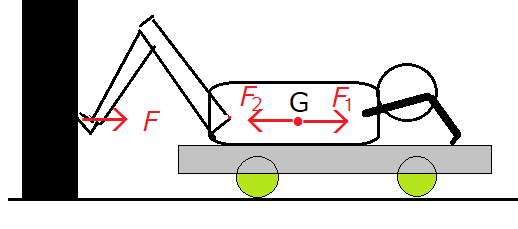
足の筋力が創り出した力学的エネルギーが、どのようにして重心運動に供給されるかを説明するために、系の重心Gに、大きさがFと等しいF1とF2が図2のように働いていると考えよう。そうしても、両者は打ち消し合うので、運動に影響はない。そこで、Fの役割を、FとF1とF2の三つの力の果たす役割に置き換えて考えよう。
FとF2とを一対の力として考えると、それは足を伸ばそうとする運動を妨げる応力として働いている。つまり、 FとF2の一対の力 は足の変形運動に負の仕事をし、系の重心に働くF1が系の重心運動に仕事をする。足を伸ばす運動に仕事をするのは、足の筋力であるが、Fは、その運動に負の仕事をすることによつて系の重心運動に正の仕事をすることになる。
Fは正味の仕事をして、系にエネルギーを供給することはできないが、負と正の仕事を同時にすることによって、足の筋力の仕事によって得られた力学的エネルギーを系の重心運動に分け与えている。重心の運動方程式である1式のFの、その作用点は壁ではなく、系の重心Gであると考えるべきである。静止した状態から、人が台車の上でいくら体を動かしても、外力がなければ、体も台車も動くが、系の重心の重心は動かず、重心運動にエネルギーが生じることはない。
抗力は、その作用点が動かないので、正味の仕事をしない。しかし、だからと言って、抗力は一切仕事をしないと考えるのは短絡的である。ニュートンの運動方程式を適用して得られた1式を数学に委ねれば、あとは2式のように抗力のする仕事が自然に導かれる。数学と整合性のとれたニュートン力学の美しさだが、数式を使わない証明もまた大切である。しかし、それは運動方程式から導かれる結果と一致しなければならない。一致しないなら、するまで徹底的に深く考えなければならない。中途半端に考えたために、矛盾が生じ抜き差しならぬ状態に陥り、そこから抜け出すために、Pseudoworkのような不可解な仕事を導入するのは本末転倒である。
喜寿を迎える今日まで物理で飯を食ってきながら、運動法則の簡潔さとは対照的に、その簡潔な法則に支配されるニュートン力学の奥深さに、今回の論争を通して気づかされた。賛否に関わらず、ご意見を寄せて頂いた方々に深く感謝したい。

コメント