三体問題
ニュートンの万有引力の法則によれば、二つの天体には、両者の質量の積に比例し、天体間の距離の2乗に反比例する引力が働く。つまり、質量がそれぞれm1とm2の天体1と天体2が距離rだけ離れているとき、両者に働く万有引力の大きさは、Gm1m2/r2となる。Gは自然界の普遍的な定数であり、万有引力定数と呼ばれている。 二つの天体からなる系の運動方程式は解析的に解けるが、三つの天体からなる3体問題の運動方程式は、一般には解析的に解けず、三つの天体の運動は予測不可能なカオスになる。
三体問題の重心
三つの天体の位置ベクトルを、それぞれ、r1,r2,r3とし、3天体系の重心の位置ベクトルをr0とすると、重心の定義から、r0は、
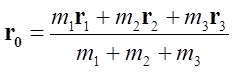
と表される。天体系の外部から、各天体に働く力は存在しないとすると、系の重心は、最初、静止していれば、静止したままだから、座標の原点を3天体系の重心に選べば、r0=0であり、
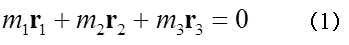
となる。
正三角形解
三体問題は一般にはカオスとなるが、三つの天体が正三角形の頂点に位置するとき、三天体はその形状を保つことができる。辺の長さがαの正三角形の頂点に位置しているとすれば、
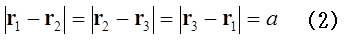
が成り立つ。天体1は、天体2と天体3からそれぞれの方向に万有引力によって引っ張られるから、天体1に働く万有引力f1は、それら二つの万有引力の和であるから
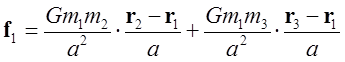
となる。(1)式が成り立つことから、f1は簡単になり
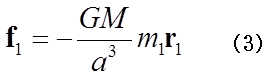
と表される。ここで、M=m1+m2+m3である。同様に、天体2や天体3にも他の二つの天体から働く力は
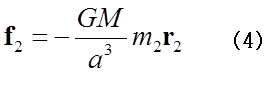
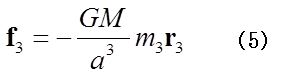
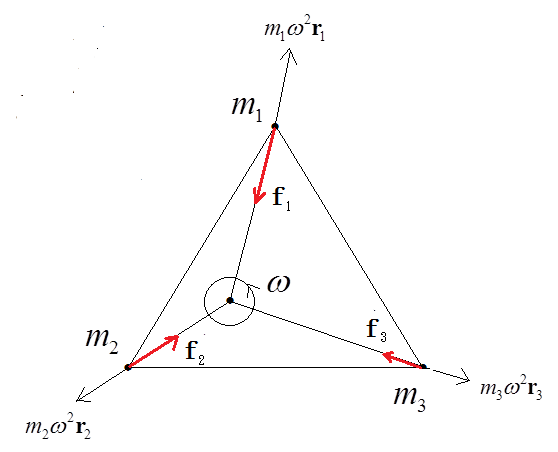
となる。正三角形の頂点に位置した天体の系が、系の重心(座標の原点)のまわりに角速度ωで回転すると、図1のように、それぞれの天体に、m1ω2r1、m2ω2r2、m3ω2r3の遠心力が働く。もし、ω2=GM/α3であれば、それぞれの天体に働く遠心力と、(3)(4)(5)で表される天体に働く万有引力、f1、f2、f3 とが釣り合うことができる。
ω2がGM/α3 より大きければ、三天体の位置は正三角形を保ったまま、 ω2=GM/α3 が成り立つまで辺の長さαが大きくなり、逆に ω2がGM/α3 より小さければ、辺の長さが短くなる。これを三体問題の正三角形解という。
直線解
直線上に、三つの天体が一定の条件をみたすように配置したとき、一つの天体に、他の二つの天体が及ぼす引力と回転座標の遠心力とが釣り合うことができる。三つの天体が、直線上に、天体1、天体2、天体3の順に配置したとき、天体1と天体2の距離をr12 、天体2と天体3の距離をr23とし、 z=r23/r12 が、5次方程式、
(m1+m2)z5+(3m1+2m2)z4+(3m1+m2)z3-(m2+3m3)z2-(2m2+3m3)z-(m1+m2)=0 (6)
を満たすとき、計算の詳細は省略するが、三つの天体のそれぞれについて、他の二つの天体から受ける引力と座標系の引力とがつりあうことが証明できる。これを三体問題の直線解という。
ラグランジュ・ポイント
地球の公転軌道を完全な円と仮定し、三つの天体として、太陽と地球と小天体を選ぶと、小天体の質量が太陽や地球の質量に比べ、十分小さいとすれば、小天体の運動は太陽や地球から影響を受けるが、逆に小天体が太陽や地球の運動に影響を及ぼすことはない。回転座標系の中に、小天体に働く、太陽の引力と惑星の引力と、回転座標系の回転による遠心力とがつりあう点が、図2のように5か所存在することがわかる。この五つの点はラグランジュ・ポイントと呼ばれている。図2のL4とL5が正三角形解であり、太陽と地球と正三角形をなす場所である。それに対し、L1~L3が直線解である。
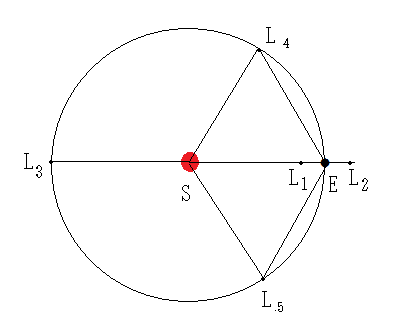
正三角形解のL4とL5は地球の公転軌道上にあるが、直線解のL1は地球の公転軌道の内側にあるがL2は公転軌道の内側にある。L3は地球軌道の僅か外側に存在する。ケプラーの第3法則によれば、惑星の公転半径が短いほど、その公転周期は短い。小天体をL1に置いた場合とL2 に置いた場合を比べると、小天体に地球の引力が働かなければ、L1は地球の公転に先行し、L2は地球に遅れることになるが、地球の引力はL1の小天体には太陽の引力と逆向きであり太陽の引力を弱めることになり、L2では両者は同じ向きだから引力が強め合う。太陽の引力が地球の引力によつて弱められれば、軌道半径は長くなることを意味し、強められれば軌道半径が短くなることと同じである。つまり、L1と地球とL2は同じ周期で公転する。L3は地球から遠いので地球の引力の効果も小さい。
直線解のL1とL2は地球に最も近いラグランジュ・ポイントであり、どちらも、地球から約150万km離れている。これら二つの位置では、小天体に働く地球の引力と、小天体を地球から引き離そうとする太陽の潮汐力とが釣り合う位置である。月の地球からの距離は38万kmとL1やL2に比べ遥かに地球に近い。月に働く太陽の引力は、地球の引力の約2倍であるにもかかわらず、地球と月の系に働く太陽の潮汐力は弱く、月が現在の距離を保っていれば、地球から引き離されることはない。→宇宙の浮舟

コメント