1.ピタゴラスの定理とは
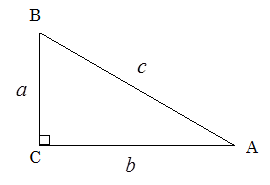
最近では三平方の定理と呼ばれることが多いが、ピタゴラスの定理は直角三角形の三辺の長さの間に成り立つ関係式であり、直角を挟む二つの辺の長さの2乗の和が、直角の対辺(斜辺)の長さの2乗に等しくなるという定理である。
つまり、図1のように、直角三角形の三つの辺の長さに次の式が成り立つ。
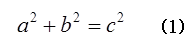
直角三角形をつくるa,b,cの組み合わせとしては、3,4,5や、5,12,13などの整数の組み合わせがある。無理数も含めれば、1,1,√2や1,√3,2の組み合わせがあり、いずれも(1)式を満たす。
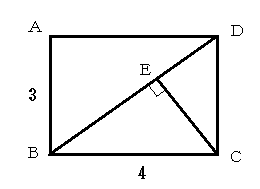
例題1 図2のように、AB=3,BC=4の長方形ABCDの対角線BDにCから下した垂線の足をEとしたとき、三角形ABD,三角形ECB,三角形EDCの面積の比を求めよ。
中学数学で習うピタゴラスの定理を用いれば、瞬時に解けよう。大、中、小の三つの三角形はいずれも相似な直角三角形であるから、面積の比は相似比の2乗である。中と小の直角三角形の斜辺の長さは4と3であり、大の直角三角形の斜辺は長方形の対角線であるから、その長さはピタゴラスの定理から5である。すべての斜辺の長さが求められたので、大、中、小三つの直角三角形の面積比は25:16:9である。
2.ピタゴラスの定理の証明
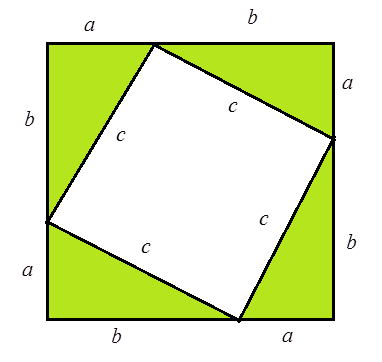
百通り以上の証明法が知られているが、その一つを紹介しよう。合同な四つの直角三角形を図3のように、並べると、一辺がa+bの正方形と、その内部に一辺がcの正方形の隙間ができる。
図3から次の等式が成り立つ。
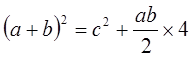
この式の左辺を展開すれば、(1)式が成り立つことが分かる。
3.ピタゴラスの定理とヒポクラテスの定理
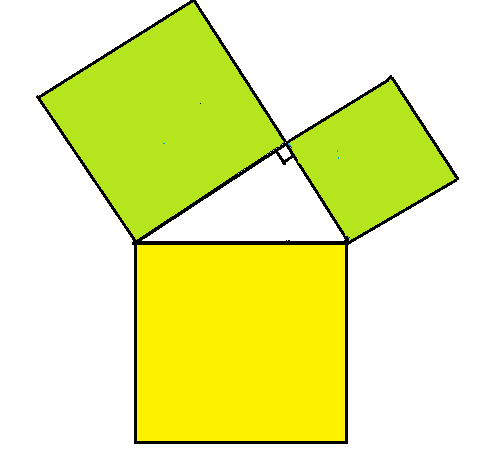
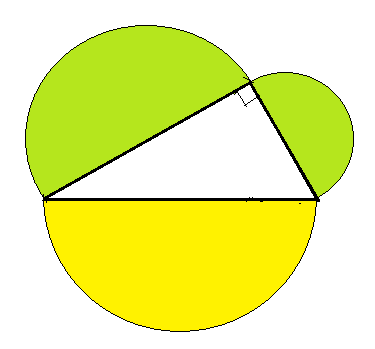
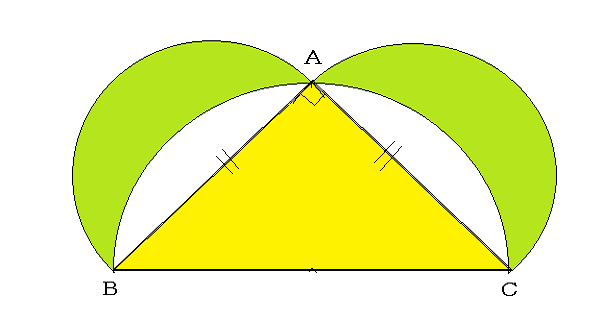
ピタゴラスの定理は図4において二つの緑色の正方形の面積の和は斜辺を一辺とする黄色の正方形の面積に等しいことを示している。それなら、正方形を、図5のように、それぞれの辺を直径とする半円に置き換えても緑色の二つの半円の面積の和は黄色の半円の面積に等しいはずである。
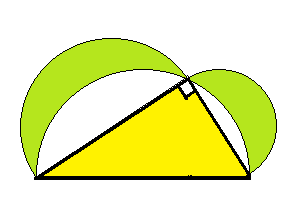
さらに、図5の直角三角形の外側に描かれた黄色の半円を、反対側に折り返して三角形側に描けば、その円周は直角の頂点を通り、直角三角形は図6のように半円に内接する。図5における二つの半円の面積の和は、図6では、二つの緑色の三日月形の面積と二つの空白の面積の和となる。それが図5の黄色い半円の面積に等しいが、それは図6では直角三角と二つの空白の面積になる。よつて、図6の二つの緑色の三日月形の面積の和は三角形の面積に等しくなることが容易にわかろう。これをヒポクラテスの定理という。
図6の二つの三日月形の面積の和には円周率が関係しそうだが、そうならずに直角三角形の面積になるのが、ヒポクラテスの定理の面白いところであろう。
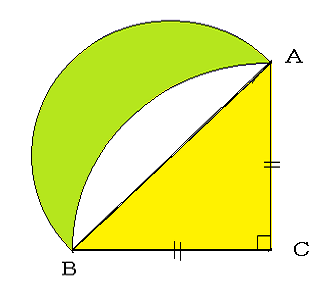
ヒポクラテスの定理を直角二等辺三角形に適用すれば、図7のようになるが、図7は左右対称だから、これを対称軸で分割すれば、図8になり、緑の三日月形の面積は二等辺直角三角形の面積に等しくなる。なお、ヒポクラテスの定理のヒポクラテスは、医学の祖と呼ばれヒポクラテスの誓いで知られる人物とは別人である。
4.ピタゴラスの定理とベクトル解析とヘロンの公式
例題2 3次元直交座標上に3点A(3,1,0)、B(2,4,1)、C(1,2,2)がある。三角形ABCの面積を求めよ。(平成19年度東京大学理学研究科地球惑星科学専攻修士課程入学試験問題)
ベクトル解析で三角形の面積は、ベクトルの外積を用いて計算できることを知っている大学生なら、簡単に解けよう。ベクトルAB=(2,4,1)-(3,1,0)=(-1,3,1)であり、同様に、ベクトルAC=(1,2,2)-(3,1,0)=(‐2,1,2)であるから、二つのベクトルの外積は(5,0,5)、その絶対値は5√2、それは、ABとACを二辺とする平行四辺形の面積に等しいので、三角形ABCの面積はその半分の5√2/2である。
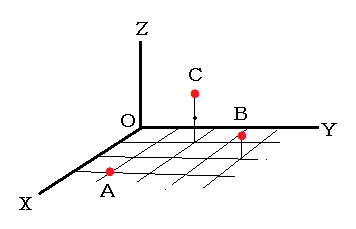
しかし、ベクトル解析を知らなくても、ピタゴラスの定理を用いれば中学生にも解ける。まず、問題の意味を理解するために与えられた3点A,B,Cの位置関係を図示すると、図8のようになる。三つの赤丸を結んだ三角形の面積を求めればよい。そのためには三角形の三辺の長さを求める必要があるが、3次元直交座標上に与えられた2点の長さもピタゴラスの定理によって求めることができる。
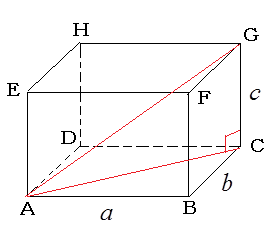
図9のような直方体ABCDEFGHにおいて、A→B→C→Gのように互いに直角三方向に、a,b,cと進んで、AからGに辿り着いたとき、AからGまでの直線距離は次のようにピタゴラスの定理を二度用いて求めることができる。まず、A→B→Cと進んだとき、直角三角形ABCにピタゴラスの定理を用いると直線距離ACを求めることができる。さらに直角三角形ACGにピタゴラスの定理を用いると、A→B→C→Gと進んだ時の直線距離AGの長さを求めることができる。つまり、
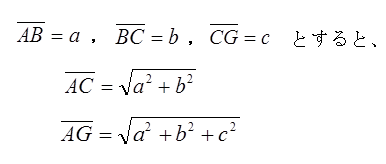
となる。これはベクトルの長さが、xyzの各の成分の2乗の和の平方根になることをピタゴラスの定理で示したことになる。そこで、もう一度図8に戻ると、三角形ABCの三つの辺の長さが中学生にも計算できることになる。計算するとその結果は図10のように、AB=√11、BC=3,CA=√6となる。
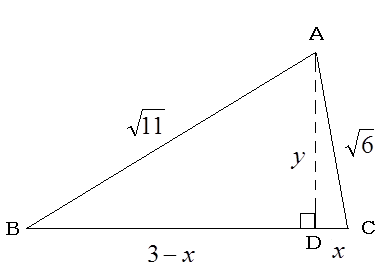
三角形の各三辺の長さが分かると、ヘロンの公式から三角形の面積が分かるが、中学数学ではヘロンの公式は習わない。しかし、この場合もピタゴラスの定理から、その三角形の面積が計算できる。AからBCに垂線を下ろし、その足をDとし、DCの長さをx,ADの長さをyとし、二つの直角三角形ABDとADCにピタゴラスの定理を用いて、xとyに関する連立方程式を解くと、y=5√2/3となるので、三角形ABCの面積は、5√2/2と求められる。これはヘロンの公式もピタゴラスの定理で証明できることを示している。
5.東大入試と円周率
「中学で習う二次方程式は実生活では、ほとんど役に立たないので教えるのをやめたがよい」とか、「円周率の近似値は3.14でなく、簡単に3にしてしまおう」とか、ゆとり教育が議論がされていた頃に、次のような興味深い問題が大学入試に出題された。これを解きながらピタゴラスの定理から円周率を計算する方法を紹介しよう。
例題3 円周率の値は3.05よりも大きいことを証明せよ。(2003年東大入試)
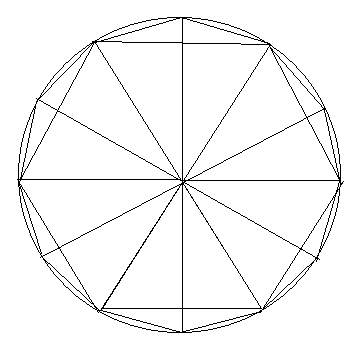
図11に示すように、正多角形を辺に沿って一周した長さ、正多角形の周の長さは角数が増えるに従い増加し、円周の長さに近づくことから、円周率の近似値を求めることができる。例えば正6角形の一辺の長さは円の半径に等しくなるので、正6角形で近似したときの円周率の値は3となる。これでは例題3を証明することはできないので、近似を上げ、正12角形にすると、半径1の円に内接する正12角形の一辺の長さは2sin15°だから、その正12角形の1周の長さは半角の公式から計算できる。円周の長さは、それより大きいことから、円周率の下限が求まる。

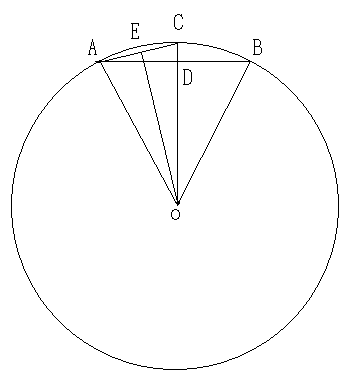
上記の解法は半角の公式を用いているが、三角関数を知らない中学生でもピタゴラスの定理を用いれば、より角数の多い正多角形を用いて真値に近い円周率の近似値を求めることができる。図12において、単位円Oの弦ABを円に内接する正n角形の辺とすれば、弦ACは円に内接する正2n角形の辺の長さになる。ABの長さが与えられれば、ピタゴラスの定理からODの長さが分かり、さらにDCの長さが分かり、直角三角形ADCにピタゴラスの定理を用いれば、ACの長さが分かる。これは円に内接する正n角形の辺の長さ分かると、同じく円に内接する正2n角形の辺の長さが分かることを示している。正6角形の周の長さから正12角形、正24角形の周の長さというように。次々に求めることができる。また、これを正4角形から出発すると、正8角形、正16角形・・・と、正多角形の周の長さを求め、円周率の精度を高めていくことができる。
6. 円周率3と3.14の違い
円周率が3でよければ、正6角形を書けば済むことだが、それを3.14の精度まで上げるには、正12角形、正24角形、正48角形、そして正98角形まで計算して、やっと3.14が現れる。3と3.14の間には数字の差以上の大きな違いがあろう。円周率の精度を筆算で3から3.14に上げるだけでも至難の業だが、江戸時代の和算家として有名な関孝和は、パソコンはおろか電卓もない時代に、なんと、正2^17角形の周の長さを求め、円周率の値を小数点以下11桁の精度で求めたという。そこで、大学のプロジェクトのJr.Dr育成塾に参加している中学生に、関孝和の計算を再現してもらい、円周率を小数点以下14桁まで計算することができた。ただし、パソコンのエクセルを使ってである。

コメント