大学院入試問題研究　3

問　x の関数y(x) が微分方程式

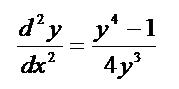
に従うとする。この微分方程式を解き、x =0において、y(0)=√2、　dy/dx=(√2)/4を満たすような関数y(x)を求めよ。微分方程式の両辺にｄｙ/ｄｘを乗じることにより、解法が簡単になることに注意せよ。（T大学大学院過去問より）

解答　与えられたヒントのように両辺にdy/dxを乗じて式を変形していくと、

式（3）の両辺をxで積分すると、

式（4）の右辺を計算すると、

与えられた初期条件から、積分定数E＝-1/4、よつて

式（6）は簡単な変数分離形の微分方程式である。初期条件を考慮して式（6）を解くと

となる。

解説　これは数学の問題だが古典力学の問題でもある。xを時間と考え、式（1）の右辺を、質量1の質点がｙ軸上で受ける力とすると、式（1）は、一次元の力の場の中を運動する質点の運動方程式と考えることができる。問題文に与えられたヒントは、運動方程式からエネルギーを求めるときの常套手段である。式（5）は質点の運動エネルギーが、力学的エネルギーEとポテンシャルエネルギーUの差に等しいことを示している。出題者の意図を見抜くことができれば簡単であろう。