2018年度秋の日本物理学会が9月9日から京都の同志社大学で開催される。折角、京都で開催されるならと、老夫婦での観光も兼ねて、学会に出席し発表することにした。発表の内容は、二年半前の仙台での学会発表以来続いている、仕事を巡る論争である。その経緯は仙台以来、HPにも書き連ねてきたことであるが、それを整理し、今回は講演題目を「物体の並進運動に力がなす仕事」として発表することにした。
観光旅行にしか関心のない愚妻は論争がいつまでも続くことを期待しているようだが、細々とした年金暮らしなのに、このまま論争が長引き、学会があるごとに、夫婦で観光旅行していては、我が家の家計は破たんする。今回の学会までが経済的には限界であろう。
学会の発表は、講演10分、質疑応答5分である。このHPが学会出席者の目に、どれだけとまるかは分からないが、また、これまでのHPの記載と重複する部分もあるが、短い時間内での議論がスムーズに進むように、あらかじめ発表の詳細をHPに載せておきたい。
1.はじめに
定年後の、終活とボケ防止のための脳活を兼ねて、エジプトのファラオも羨む巨大な墓をWeb上に造ろうと思い立って始めたホームページ作りだが、その内容の一部を日本物理学会誌(2016年2月号)の談話室に紹介したところ、賛成意見もいくらかあったが、全国の物理教育関係者の大半を相手にしての論争となった。
これ以上の脳活はないのでありがたいことだが、ことの起こりは、終活とは無縁の若い頃から抱いていた素朴な疑問に、前述の学会誌のなかで、次のように自問自答したことに始まる。
芥川龍之介の短編小説「蜘蛛の糸」において、主人公のカンダタが蜘蛛の糸を登るとき、仕事をしたのはカンダタの筋力ではなく、蜘蛛の糸の張力である。人が自転車で走るときも、仕事をするのは人の筋力ではなく、駆動輪である後輪が道路から前向きに受ける水平抗力である。
これに対して、筋力説を主張する人々、いわゆる筋力派から寄せられた反論は次のようであった。
①抗力が仕事をするなら、エネルギー保存則は成り立たない。抗力説は物理の常識に反する。
②仕事は、力とその作用点の変位との積である。蜘蛛の糸の張力も、道路からの抗力も束縛力であり、作用点が動かないので仕事はしない。
③自転車が走れるのは、抗力が仕事をするためでなく、抗力が力積として働き、系に運動量が生じるからである。
④並進運動の運動方程式を重心座標で積分して得られる仕事は真の仕事ではないという論文1)がすでに三十数年前にアメリカで発表されている。
筋力説を是とする立場からすれば、いずれも、もっともな反論であるが、力学の基本法則はニュートンの運動法則であり、その運動方程式から数学的手法で導かれる結果も真でなければならない。自転車の問題で、並進運動の運動方程式に現れるのは車輪が道路から受ける水平抗力だけである。運動方程式に現れる力が仕事をせずして何が仕事をするのだろうか?
筋力派は当然その問に筋力だと答えるであろうが、上図において、道路からの抗力がなくても、ペダルを踏めば駆動輪である後輪は回転する。しかし、抗力がなければ、いくらペダルを踏んでも、後輪は回転しても車の並進運動は起こらない。人が筋力によって自らを変形させ、直接、仕事をすることができるのは、ペダルとチェーンによって繋がっている後輪に対してだけである。筋力が後輪の回転運動に仕事をして、後輪が得たエネルギーが、並進運動にどのようにして伝わるかを説明しなければならない。そのためには抗力がする仕事が必要になる。上図の自転車の場合、抗力Fが並進運動と後輪の回転運動に、それぞれ同時に正と負の仕事をするので、エネルギーの保存則を破ることなく、後輪の回転運動から並進運動へのエネルギーの移動が簡単に説明できる。そして、並進運動が生じれば、今度は前輪に働く抗力fが、並進運動に負の仕事をし、同時に前輪の回転運動に正の仕事をするので、前輪の回転も抗力fのする仕事として説明できる。
少々の反対意見は予想していたが、抗力説に対するアレルギーが、物理学のプロ集団の間に、これほど蔓延していたとは意外な発見であったが、その理由の一つは仕事の定義についての誤解によるものであろう。仕事の定義は抗力が仕事をすることを禁じてはいない。
2.仕事の定義
岩波書店発行の広辞苑(第四版)には、仕事について、次のように記述されている。
「力が働いて物体が移動した時に、物体が移動した向きの力と、移動した距離との積を、力が物体になした仕事という。」
一方、同じく岩波書店発行の、理化学辞典(第三版)は、広辞苑と異なり、次のように記述している。
「力学系に力Fが作用し作用点がdrだけ変位するとき、スカラー積(F,dr)を、その力が力学系になした仕事という。」
広辞苑の記述のなかで、「移動した距離」とは、「物体の移動した距離」であり、さらに言えば、「物体の重心が移動した距離」である。「物体の移動した距離が」が、理化学辞典の記述のなかの「作用点の変位dr」と同じになるのは、物体が質点の場合のみであり、一般には、両者は等しくはない。広辞苑と理化学辞典の定義は、異なる仕事についての定義だと考えざるを得ない。簡単のため、広辞苑で定義されている仕事を仕事A、理化学辞典で定義されている仕事を仕事Bと呼ぶことにしよう。
それでは、他の辞典にはどのように記述されているだろうか。培風館の物理学辞典(三訂版)には、次のように記述されている。
「物体に力を加えて、物体が力の向きに移動したとき、力は物体に仕事をしたと言い仕事の量は力と移動距離の積で与えられる。」
しかし、物理学辞典の仕事の記述はこれで終わりではなく、後半部が次のように続く。
「一般には、力の向きと物体の移動の方向は必ずしも一致しないので、物体または力学系に外力Fが作用し、作用点がdsだけ変位したとき、仕事は両者のスカラー積、F・ds=Fdscosθである。ただし、θは力Fと変位dsのなす角である。」
物理学辞典の記述の前半部は仕事Aであり、後半部は仕事Bと同じである。しかし、筋力派の見解は、前半部と後半部は異なる仕事について述べたのではなく、前半部では初心者のために分かり易く記述したものであり、後半部が仕事の正確な定義であり、それが仕事の唯一の定義であるとして、物体一般に対する仕事Aの存在を否定する。
物理学辞典の前半と後半を通して読むと、筋力派の解釈のように読みとれないことはないが、易しく記述しても難しく記述しても、変形や回転可能な物体に対しては、重心の移動距離と作用点の変位とは一般には異なる。
さらに、筋力派の見解に反して、多くの高校物理の教科書にも、力学のところでは、広辞苑と同じく仕事Aだけが記述されている。但し、温度とエネルギーの箇所では、仕事は圧力と体積変化の積として定義されているから、これは仕事Bである。また大学の初年次用の物理教科書でも、当然、熱力学では仕事Bであるが、力学の箇所では仕事Aである(例えば、原康夫「物理学基礎」学術図書出版社)。
物体が質点の場合には仕事Aは仕事Bと同じになるが、高校や大学初年度の力学でも、質点のみを扱ってはいない。
言葉を定義する目的は、物事の意味や内容を他と明確に区別するためである。仕事の定義のなかに、質点と書けば質点のみを意味するが、物体と書けば、質点も含めた物体一般を意味する。これは力学以前の国語の問題である。
抗力がエネルギーを生みだすことはないが、仕事Aが一般の物体に対する仕事なら、その定義は抗力が仕事をすることを禁じてはいない。仕事Aは、質点に限定した仕事ではなく、仕事Aも仕事Bも一般の物体や系に対する仕事であり、仕事Aと仕事Bとは異なる仕事である。両者の違いは、仕事Aは、外力が、物体あるいは系の並進運動(重心運動)にする仕事であり、仕事Bは、外力が物体全体あるいは系全体にする仕事である。
抗力説にしても、並進運動のエネルギーの出所は筋力であることには違いないので、日常会話なら、自転車の並進運動に仕事をしたのも筋力でよいだろう。しかし、力学の議論では、自転車の並進運動に仕事をしたのは道路からの摩擦力と考えるべきである。
3.熱力学における仕事
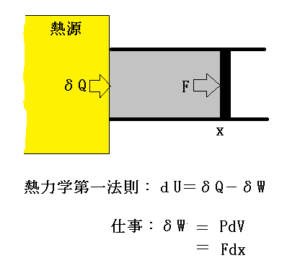
力学の基礎方程式がニュートンの運動方程式であるのに対し、熱力学の基礎方程式はエネルギー保存則である。無数の構成要素からなる系を対象とする熱力学では、個々についての運動方程式まで遡ることは不可能であり、系全体のエネルギー保存則からスタートする。
系の内部エネルギーの増分をdU、系外から系に入ってきた熱エネルギーをδQ、系が外部にした仕事をδWとすれば、熱力学の基礎方程式である熱エネルギーまで含めたエネルギー保存則は、はdU=δQ-δWと表わさせる。内部エネルギーとは、構成する分子の並進運動のエネルギーも、回転のエネルギーも、振動のエネルギーも、すべて含めたエネルギーであるから、熱力学での仕事は当然仕事Bでなければならない。しかし、系の並進運動を考えない熱力学では仕事Aが登場することはない。
 4.力学における仕事
4.力学における仕事
一方、力学では仕事Aも仕事Bも必要となる。次の図のように円柱に巻いた糸を引っ張り円柱を転がす問題を考えてみよう。 この時の運動方程式は円柱の重心の運動方程式と円柱の回転の運動方程式に分離して表すことができる。二つの運動方程式を、円筒が滑らないと言う束縛条件のもとで解けばよい。
この時の運動方程式は円柱の重心の運動方程式と円柱の回転の運動方程式に分離して表すことができる。二つの運動方程式を、円筒が滑らないと言う束縛条件のもとで解けばよい。
並進運動の運動方程式は![]() であり、回転の運動方程式は
であり、回転の運動方程式は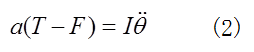 である。両者をそれぞれ重心座標で積分すれば、
である。両者をそれぞれ重心座標で積分すれば、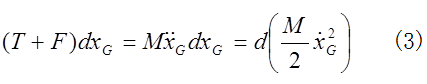
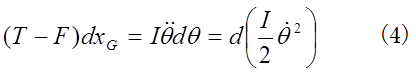 となる。抗力Fは並進運動に正の仕事をしているが、同時に、回転運動に負の仕事をしている。(3)と(4)を加えれば、
となる。抗力Fは並進運動に正の仕事をしているが、同時に、回転運動に負の仕事をしている。(3)と(4)を加えれば、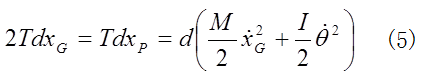 となり、系全体にする仕事は、力Tとその作用点の移動距離の積であるから仕事Bである。系全体に対する仕事であれが仕事Bであるが、その明細を知るには仕事Aが必要である。
となり、系全体にする仕事は、力Tとその作用点の移動距離の積であるから仕事Bである。系全体に対する仕事であれが仕事Bであるが、その明細を知るには仕事Aが必要である。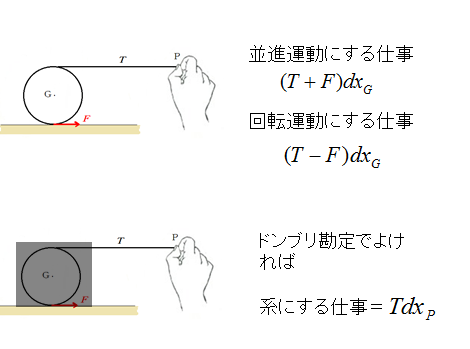 自転車の問題も、並進運動の運動方程式を重心座標で積分すれば、仕事Aと、並進運動が得たエネルギーとの関係が得られ、時間で積分すれば、力積と運動量との関係が得られる。しかし、筋力派の主張③は、運動量は力積で増えるが、並進運動に仕事をするのは筋力だと言う。これでは一貫性を欠き、木に竹を接ぐことになる。並進運動における、仕事とエネルギーの関係も力積と運動量の関係もニュートンの運動方程式から導かれるべきである。
自転車の問題も、並進運動の運動方程式を重心座標で積分すれば、仕事Aと、並進運動が得たエネルギーとの関係が得られ、時間で積分すれば、力積と運動量との関係が得られる。しかし、筋力派の主張③は、運動量は力積で増えるが、並進運動に仕事をするのは筋力だと言う。これでは一貫性を欠き、木に竹を接ぐことになる。並進運動における、仕事とエネルギーの関係も力積と運動量の関係もニュートンの運動方程式から導かれるべきである。
5.おわりに
系の並進運動を考えない熱力学では、仕事Aは必要ないが、ボールや人や車の運動など、物体の並進運動が第一義的である場合は、仕事Bだけでは不十分であり、むしろ、仕事Bより仕事Aが必要不可欠な仕事になる。
前述の、30数年前にアメリカで発表された論文の著者は、仕事Aには、抗力のする仕事が含まれるので、真の仕事でなく、pseudoworkだと主張している。筋力派の主張には、アメリカのその論文が強い影響力を及ぼしているようだが、古典力学は、その基礎とすべきはニュートンの運動方程式であり、アメリカの論文ではない。仕事Aは運動方程式に則った仕事であり、仕事Bは熱力学第一法則に則った仕事であり、両者とも互いに独立な真の仕事である。抗力が仕事をする場合、正と負の仕事が一対となって、必ず同時に現れるので、抗力が仕事をすると考えても、第一法則に矛盾しない。これまでの教科書や辞典の記述を変更する必要はない。力学においては、ドンブリ勘定の筋力説よりも抗力説のほうがはるかに優れている。→ブランコとボタフメイロ
1)Bruce Arne Sherwood: Pseudowork and real work, , Am.J. Phys.,Vol.51, 1983
予告! 学会発表
 力学
力学
コメント