長崎は、サカとハカとバカが多い街だよ。 長崎大学に赴任してきたとき、先輩からそう教わった。バカとは祭りバカのことだそうだが、確かに長崎は、坂が多く、山の斜面に造られた墓地は遠くからも目立ち、祭りの期間は旧長崎の市街地では、街全体が賑わい盛り上がる。しかし、長崎に住み街を「さるく」と、坂や墓よりも、はるかに多いものが存在していることを発見した。
「さるく」とは、長崎の方言で、あちこち、歩いてうろつき回ることだが。別の方言に言いかえれば、さしたる目的もなく「ほっつき歩く」ことであり、長崎のみならず、佐賀、福岡、熊本の四県にまたがる有明海沿岸一帯でも通じていたようである。昔は土地と土地とが、陸路より海路で繋がっていた名残であろう。
どこをさるいても、パチンコ店が多いのは全国共通のようだが、他ではあまり見られず長崎に多い特徴的なものと言えば、カステラ店、中華料理店、坂道、石橋、寺、教会などだろうか。しかし、それらより遥かに多いものが長崎には存在する。
長崎市街を10mも歩けば、確実に目にする、あるもののなかに隠れているが、車で通り過ぎるだけでは発見するのは難しく、長崎でも一般には、その存在はほとんど知られていない。
安政年間に、函館、横浜、新潟、神戸と並んで開港された五港の一つが長崎港であることから、長崎市の市章として五芒星が採用されているため、長崎をさるくと、あちこちに図1のような五芒星の描かれたマンホールが見られるが、その五芒星の中に隠れている。

長方形のなかで、一番美しい図形は、縦横の長さの比が黄金比になっている長方形とされるが、長崎市の歩道のマンホールに描かれている五芒星を見つめていると黄金比を発見できよう。
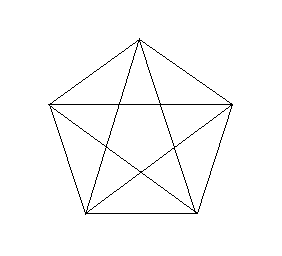
図2のように、正五角形の頂点をつないだ図形から、最初の正五角形の五つの辺を消し去ると、☆印の図形ができ、五つの光芒が出ている星、それが五芒星と呼ばれる図形である。そのなかの、図3のような二等辺三角形に注目すると黄金比が見えてこよう。
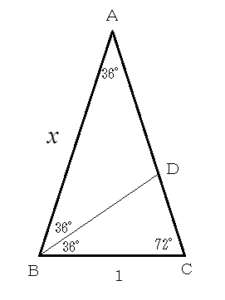
二等辺三角形ABCは頂角が36°で、底辺と側辺の長さの比が黄金比になっている。頂角Aが36°だから、両底角BとCは72°であり、頂角の二倍だから、角Bの二等分線と辺ACの交点をDとすると、⊿BCDも頂角が36°、両底角が72°の二等辺三角形となる。⊿ABCと⊿BCDは相似であり、次の式が成り立つ。
AB:BC=BC:CD
AB=AC=、BCの長さを1とすれば、CD=AC-AD=
-1だから、
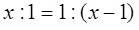
となり、これから二次方程式
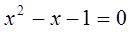
が導かれ、方程式の二つの解のうち、正の解を選べば
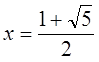
となる。これは黄金比に等しくなり、=1.618・・・・・となる無理数である。黄金比については、さらに「黄金分割とフィボナッチ数列」を参照。
長崎に一番多いのは坂でも墓でもなく、黄金比ということになるが、話はこれだけで終わらないところが長崎である。長崎の中心街、浜の町のアーケード街の一箇所にだけ、図4のような六芒星のマンホールがある。当然、この図形に黄金比は存在しない。
長崎の観光ガイドマップ、「長崎さるく」には、その場所を長崎で唯一、六芒星のマンホールが存在するミステリーゾーンとして紹介されている。どうして、このマンホールにだけ、ダビテの星とも呼ばれる、ユダヤ教を象徴する六芒星が描かれているのか、それについては諸説あり、本当のことはよく分かっていないとのことである。もしかしたら、黄金の在処を示した暗号だろうか。

単に市章のデザインの光芒の数を間違えただけで、そこをいくら掘り起こしても、黄金も財宝も出てこないと思うが、さすが観光都市長崎、転んでもタダでは起きぬその根性、見上げたものでである。
長崎の 街をさるけば 間違いも
名所のなかに 繰り入れられて
ここで、正五角形に関する数学の問題を一つ。次の図の正五角形FGHIJおよび三角形AIHの面積は、それぞれ、正五角形ABCDEの面積の何倍か。(T大大学院修士課程入試問題より)
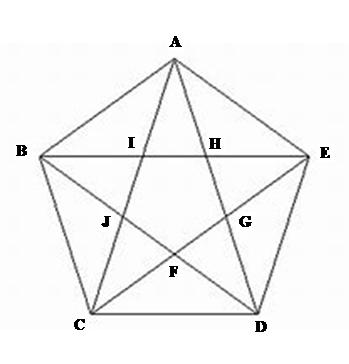
なに難しい? 黄金比の街、長崎に生まれ育ったのなら、この程度の問題、簡単に解かんば! と、檄を飛ばして、Jr.Dr育成塾(長崎大学のプロジェクト)に参加している生徒に解かせている。
ヒント:黄金比をとすると、正五角形ABCDE=
×正五角形FGHIJ、
など。

コメント