LCR回路とエネルギー

大学院入試過去問より
起電力 $E$ の電源、インダクタンス $L$ のコイル、抵抗 $R$ 、静電容量 $C$ のコンデンサー、スイッチ ${ S }_{ 1 }$ 　、 ${ S }_{ 2 }$ 　、および ${ S }_{ 3 }$ よりなる下図のような回路に関し、以下の問いに答えよ。
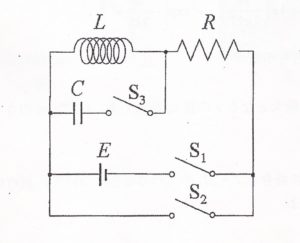
問1．スイッチ ${ S }_{ 1 }$ を閉じた場合の電流 $J$ の時間変化を表わす微分方程式を示せ。次に、これを解き、かつ $J$ の時間変化を図に示せ。
解：　 $LR$ の直列回路であるから、微分方程式は、
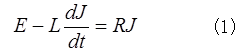となる。よつて、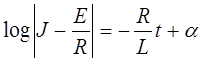初期条件は、 $t=0$ のとき、 $J$ ＝0であるから、積分定数αの値はlog(E/R)となる。よつて、（1）の解は
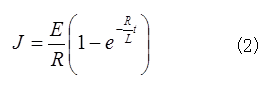
電流 $J$ の時間変化の図は省略するが、時間ｔが増えるに従い、 $J$ は、ゼロの値から増加率 $E/L$ で増えはじめ、次第にその増加率は減少して、やがてゼロとなる。つまり（2）から $J$ の値は一定値 $E/R$ に収束することが分る。
問2．問1の微分方程式をエネルギーの収支を表わすように変形し、各項の物理的意味を、それぞれ、10字程度で説明せよ。また、時刻Ｔにおいてコイルに蓄えられた磁場エネルギーW_Lを求めよ。
解：（1）式より、
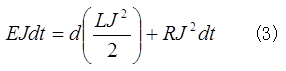左辺は電池から回路に供給されるエネルギー、右辺第1項はコイルに蓄えられる磁場のエネルギー、右辺第2項は抵抗でジュール熱として消費されるエネルギー
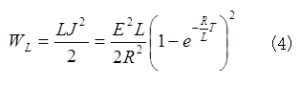問3．さらに長時間経過して平衡に達した後、Ｓ₁を開けると同時に₂を閉じた場合の電流Jの時間変化を表わす微分方程式を示せ。次に、これを解き、かつJの時間変化を図に示せ。
解：これも微分方程式とその一般解は
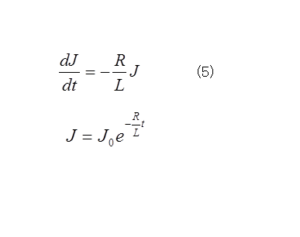となる。ｔ＝0で、抵抗Rにかかる電圧はEであるから、J₀＝E/R　よって解は
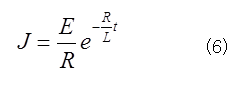これも図を省略するが、Jは初期値E/Rから指数関数的に減少し、充分時間が経過した後では0となる。
問4．S₂を閉じて長時間経過して、平衡に達するまでの間に、抵抗で発生した熱エネルギーW_Rを求めよ。また、問3において平衡に達した時点のW_Lと、ここで求めたW_Rを比較し、その物理的意味を30字程度で述べよ。
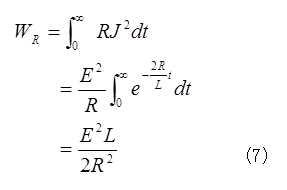これは（4）式においてＴ→∞トした場合のW_Lと一致する。
問5．S₂を開いた後、再びS₁を閉じ、長時間経過して平衡に達した後、S₁を開けると同時にS₃を閉じた場合、コンデンサーに現れる最大電圧を求めよ。
解：ＬＣ振動回路となるから、最初コイルが持っていたエネルギーが全てコンデンサーのエネルギーになったとき、コンデンサーの電圧は最大となる。
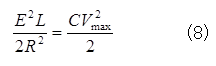よつて、
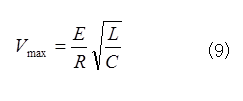となる。計算間違いをしていなければ以上で多分正しいだろう。
解説
LR回路の微分方程式（1）は、レンツの法則に従い電流の変化を妨げる向きにコイルに起電力が生じることを理解しておれば、簡単に導けよう。方程式も簡単な変数分離系であるから、あとは、問2、問3と、順を追っていけば容易に解けよう。問5は振り子を連想すると分かり易い。振り子の場合に、その運動エネルギーの最大値とポテンシャルエネルギーの最大値とが等しいのと同じである。