大学院入試過去問より①
図のように、原点Oを中心とする、半径1の球面上の四角形、つまり、球面四角形ABCDの対角線の交点をPとする。対角線、ACおよびBDは、いずれも大円に沿った測地線とする。Pおよび、A、B、C,Dの位置ベクトルをそれぞれ、p、a、b、c、dとする。pをa、b、c、dを用いて表せ。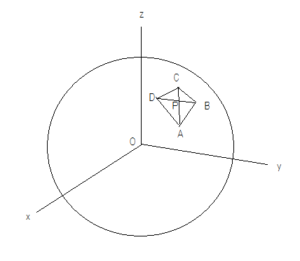
ヒント:一見難しいが、この問題は、ベクトルpが3点O、A、Cを含む平面αと3点O、B、Dを含む平面βの交線上にあることに気づけば簡単である。
解答
平面αに垂直なベクトルαはベクトル積a×cと表わされ、平面βに垂直なベクトルβはb×dである。さらに、ベクトルpはαとβの両方に垂直であるから、![]() となる。pは単位ベクトルであるから、規格化して
となる。pは単位ベクトルであるから、規格化して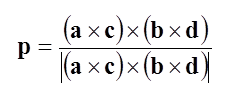 となる。
となる。

コメント