1.束縛力がない場合
質点AとBは、ともに質量がmで、どちらも帯電し正の電荷qを持ち、さらに、最初は、質点AとBとが長さ2y0の糸で結ばれているとする。AとBとはクーロン力で反発しあうので、糸には張力が働き、それはAB間の電気的反発力の大きさfに等しい。 fおよび、この系の静電エネルギーE は、それぞれ、f=k/2y02および、E=k/y0となる。ただし、k=q2/8πε0とする。
ある瞬間にAとBを繋いだ糸が切れると、静止していた二質点は互いに反対方向に速さを増しながら動き始める。AB間の距離が2yのとき、質点Aの運動方程式は、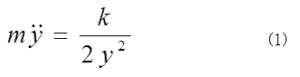 yがLになったときのAの速さをvとして、(1)式をyでy0からLまで積分すると、
yがLになったときのAの速さをvとして、(1)式をyでy0からLまで積分すると、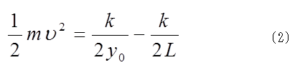 質点Bについても、同様に(2)式が導かれるので、(2)式の両辺を2倍すると、左辺は系の運動エネルギーであり、右辺はAとBの間隔が2y0から2Lに広がったために解放された静電エネルギーとなる。充分、時間が経過すると、系の静電エネルギーがすべて解放され、二つの質点の運動エネルギーに変わる。AとBの最終的な速度の大きさは、(2)式から、一定値(k/my0)1/2となることが分かる。しかし、系の重心は動かない。内力fは系全体の運動に対しては仕事をするが、系の重心運動に対しては仕事をしないことを示している。
質点Bについても、同様に(2)式が導かれるので、(2)式の両辺を2倍すると、左辺は系の運動エネルギーであり、右辺はAとBの間隔が2y0から2Lに広がったために解放された静電エネルギーとなる。充分、時間が経過すると、系の静電エネルギーがすべて解放され、二つの質点の運動エネルギーに変わる。AとBの最終的な速度の大きさは、(2)式から、一定値(k/my0)1/2となることが分かる。しかし、系の重心は動かない。内力fは系全体の運動に対しては仕事をするが、系の重心運動に対しては仕事をしないことを示している。
2.抗力のある場合
 水平な台上に半径R(R>y0)の円形の枠が固定されている。枠の中心を原点として座標系を図1のように選び、枠の内側に、1.で用いた、長さ2y0の糸で繋がれ、かつ帯電した質点ABを、糸がy軸に平行で、AとBが枠に接するように置くと、AとBの座標はそれぞれ、(x0,y0)、(x0,-y0)となる。この状態では枠からの抗力は働かない。
水平な台上に半径R(R>y0)の円形の枠が固定されている。枠の中心を原点として座標系を図1のように選び、枠の内側に、1.で用いた、長さ2y0の糸で繋がれ、かつ帯電した質点ABを、糸がy軸に平行で、AとBが枠に接するように置くと、AとBの座標はそれぞれ、(x0,y0)、(x0,-y0)となる。この状態では枠からの抗力は働かない。
 時刻t=0 に糸が切れると、それ以後AとBには内力fと、枠からの抗力Fが働く。時刻tにおけるAの座標を(x,y)とすると、Bの座標は(x,-y)である。また、極座標で表すと、x=Rcosθ、y=Rsinθである。このときの質点Aの
時刻t=0 に糸が切れると、それ以後AとBには内力fと、枠からの抗力Fが働く。時刻tにおけるAの座標を(x,y)とすると、Bの座標は(x,-y)である。また、極座標で表すと、x=Rcosθ、y=Rsinθである。このときの質点Aの
x方向の運動方程式は、![]() y方向の運動方程式は、
y方向の運動方程式は、![]() 束縛条件は
束縛条件は![]() (3)式と(4)式を、それぞれ、点(x0,y0)から点(xA,yA) まで、軌道に沿って座標積分して加えると、
(3)式と(4)式を、それぞれ、点(x0,y0)から点(xA,yA) まで、軌道に沿って座標積分して加えると、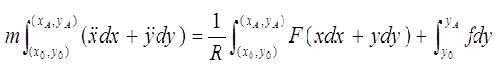 束縛条件(5)より、xdx+ydy=0だから、右辺第1項は0となる。よつて、
束縛条件(5)より、xdx+ydy=0だから、右辺第1項は0となる。よつて、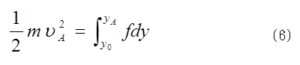 f=k/2y2であるから、(6)式の右辺は1/2(k/y0-k/yA)となる。質点Bについても同様であるので、(6)式を2倍すると、左辺は系の運動エネルギーであり、右辺は系の静電エネルギーの減少分に等しいことを示している。つまり、
f=k/2y2であるから、(6)式の右辺は1/2(k/y0-k/yA)となる。質点Bについても同様であるので、(6)式を2倍すると、左辺は系の運動エネルギーであり、右辺は系の静電エネルギーの減少分に等しいことを示している。つまり、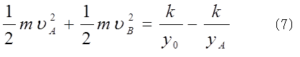
3.抗力の役割と重心運動
(6)式は、抗力が存在する場合も、系の運動に仕事をするのは内力であり、抗力は系の運動には仕事をしないことを示しているが、系の運動を重心運動と重心に対する相対運動に分解すれば、抗力はその両方の運動に仕事をすることができる。今の場合、相対運動とは、AB間の距離が伸びる変形運動である。 重心Gの座標は(x、0)である。M=2mとし、系に働く力を平行移動し、力の作用点を重心に移動すると、図3より、重心の運動方程式は
重心Gの座標は(x、0)である。M=2mとし、系に働く力を平行移動し、力の作用点を重心に移動すると、図3より、重心の運動方程式は
![]() ここで、質点の数が2だから、(8)式は(3)式を2倍しただけとなっているが、物理的な意味は(3)式とは異なる。(3)式は質点Aの運動方程式のx成分であるが、(8)は質点系の重心の運動方程式である。Fもθもxの関数であり、(8)式の両辺をxで積分すると、
ここで、質点の数が2だから、(8)式は(3)式を2倍しただけとなっているが、物理的な意味は(3)式とは異なる。(3)式は質点Aの運動方程式のx成分であるが、(8)は質点系の重心の運動方程式である。Fもθもxの関数であり、(8)式の両辺をxで積分すると、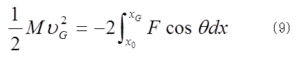 二つの抗力のx成分が仕事をすることによって、重心は運動エネルギーを得ている。
二つの抗力のx成分が仕事をすることによって、重心は運動エネルギーを得ている。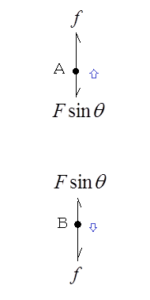 一方、重心から見たAおよびBの運動には重心運動と逆向きの慣性力が加わるので、AやBに働く力のx成分は消える。つまり、重心系座標系では、左図のように、AもBも重心もx方向には動かない。Aは+y方向、Bは-y方向に動くので、fは相対運動に正の仕事をするが、抗力Fのy成分は負の仕事をしている。つまり、AとBに働く抗力は相対運動から正のエネルギー、2Fsinθdy=2Fydy/Rを貰っている。これは束縛条件xdx+ydy=0から、-2Fxdx/Rに等しく、さらに、-2Fcosθdxとなり、(9)式において抗力が重心運動にした仕事に等しい。
一方、重心から見たAおよびBの運動には重心運動と逆向きの慣性力が加わるので、AやBに働く力のx成分は消える。つまり、重心系座標系では、左図のように、AもBも重心もx方向には動かない。Aは+y方向、Bは-y方向に動くので、fは相対運動に正の仕事をするが、抗力Fのy成分は負の仕事をしている。つまり、AとBに働く抗力は相対運動から正のエネルギー、2Fsinθdy=2Fydy/Rを貰っている。これは束縛条件xdx+ydy=0から、-2Fxdx/Rに等しく、さらに、-2Fcosθdxとなり、(9)式において抗力が重心運動にした仕事に等しい。
しかし、抗力が仕事をするという考えに反対する人々がいる。彼らは図3において重心が左方に動くのは、抗力の力積のためだと主張する。それ自体は正しいが、系が受けた力積が系が運動量になることを説明したに過ぎない。重心運動のエネルギーを計算するには重心の運動方程式を重心座標で積分しなければならないが、その積分に何の問題もない。図3に示されるように、Fはもはや質点AやBに働く抗力ではなく、重心に働く力だからである。
アメリカで1983年に発表された論文Pseudowork and real work
では、(8)式を座標で積分した(9)式の右辺は抗力がした仕事に等しいことを認めているにも関わらず、力が抗力だから、真の仕事ではないとしている。しかし、(8)式には、系の回転や変形は含まれてはいない。(8)式は重心の運動方程式なのに、そこに登場する力が重心以外の点に作用していると考えては支離滅裂な議論となろう。(9)式の右辺も真の仕事と考えるべきである。Pseudoworkの考えには何のご利益もなく、学生を混乱させるだけである。
4.おわりに
時刻0に、1点(x0,0)から初速0で、x軸上を負の方向に加速しながら動き始めた系の重心は、原点0を過ぎると減速に転じ、(-x0,0)に来ると、正の方向に向きを変え、原点に向かって加速し、xの正の領域にくると減速する。重心の加速や減速は、抗力が重心運動に正や負の仕事をすることによって起こる。重心運動が加速するとき、AとBの間隔は伸び、電気的エネルギーは減少する。逆に重心運動が減速するときは間隔は狭まり電気的エネルギーが増す。重心運動のエネルギー、AB間の屈伸運動の運動エネルギー、屈伸運動に伴う電気的エネルギーの和が、枠からの抗力が重心運動と、屈伸運動の両方に、正と負の仕事をすることによって一定に保たれている。
これは電気自動車においてアクセル踏んで発進したり、ブレーキを踏んで減速する場合と同じである。動輪が受ける道路からの水平抗力、即ち静止摩擦力のする仕事によつて、力学系と電気系との間でエネルギーのやり取りが行われる。
に
クーロン力で反発する2質点系
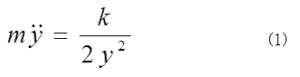 力学
力学
コメント