1.はじめに
芥川龍之介の小説「蜘蛛の糸」で、蜘蛛の糸を登るのに仕事をしたのは、物語の主人公カンダタの筋力（筋力説）か、それとも蜘蛛の糸の張力（張力説）と考えるべきかが論争になった1,2,3)。まず、二つの説を紹介しておこう。
筋力説：カンダタに働いている力は、上向きに働く張力と下向きに働く重力である。カンダタがぶら下がったまま、何もしなければ、張力と重力とが釣り合い、カンダタの重心は上にも下にも動かない。しかし、つり合った状態から、カンダタが掴んだ糸をグイと下に引っ張れば、重力は一定のままで、糸の張力が増すので、力のつり合いが破れ、カンダタの重心は上方に移動する。この動作を繰り返しカンダタは糸を登る。糸を引っ張るには、カンダタは筋力で体を収縮させなければならない。仕事をしたのは筋力であり、張力は束縛力であり、作用点が動かないので仕事はしない。
張力説：カンダタの運動を、重心運動と重心の周りの運動に分けて考えることができる。前者の重心運動は重心に質量が集中していると考えるので質点の運動と同等である。後者の重心の周りの運動とは、この場合には主に屈伸運動である。カンダタの筋力は仕事をすることによって、屈伸運動にエネルギーを補給し、糸の張力は、屈伸運動に負の仕事をすることによって、カンダタの重心運動に正の仕事をすると考えられる。張力は、束縛力だから、正味の仕事をすることは出来ないが、屈伸運動をとおして、筋力からエネルギーの「後方支援」を受け、重心運動に仕事をする。
運動方程式も、それを解く数学も必要とせず、力のつり合いの破れから重心の移動を説明する筋力説は確かに簡単で理解しやすいが、何か物足りない。それに対して張力説は、カンダタの運動を二つの運動に分解して考えるので、一見、複雑であるが、カンダタの体内で作られたエネルギーが、どのようにして、重心運動のエネルギーに変わるのか、そのしくみがよく分かる。
そこで、張力説を、複数の物理関係のメーリングリストで紹介したところ、予想はしていたが、「束縛力は作用点が動かないので仕事をするはずはない」「張力が仕事をするなら、カンダタは疲労しないで登れることになり、常識に反するではないか、話にならん！」と、いずれのメーリングリストでも非難轟々、四面楚歌であった。
二説ともエネルギー源は筋力だから、筋力説を否定するつもりはないが、束縛力は本当に一切仕事をしないのだろうか。張力説への反対意見（例えば、鈴木亨：「蜘蛛の糸」とPseudowork)が大勢を占めるなか、千万人と雖も吾往かんと、敢えて張力説を提唱した者として、張力説に対する世の批判に、少し数式に重きをおいて答えたい。
2.自転車に乗ったカンダタ
カンダタが蜘蛛の糸を登る問題は、カンダタが自転車に乗って坂道を登る問題と等価である。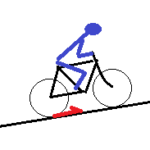
つまり、カンダタと自転車からなる系の重心運動に仕事をしたのはカンダタの足の筋力か、それとも、自転車の後輪が坂道から受ける摩擦力かということになるが、それを考えるまえに、まず、斜面を登る円筒の問題を考えてみよう。
図1のように、傾斜角θの斜面を、質量M、半径a、中心軸のまわりの慣性モーメントIの円筒が、その慣性のエネルギーだけで転がりながら登るとする。
斜面に平行で登る向きに座標のx軸、斜面と垂直上向きにy軸をとり、円筒が斜面から受ける摩擦力の大きさをF、垂直抗力の大きさをRとすると、x方向およびｙ方向の重心の運動方程式は、それぞれ、
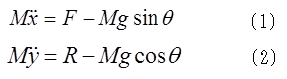
蛇足ながら、円筒の運動は重心運動と回転運動に分解して考えることができる。（1）および（2）は円筒そのものの運動方程式ではなく、分解したうちの、重心の運動方程式である。物体の重心は質点の一例である（培風館出版の物理学辞典の質点の項目）から、この二式は質点の運動を表わす式であり、FやRも重心という質点に働く力である。
一方、円筒の回転角をφとすると、円筒の回転の運動方程式は、
このとき、円筒の中心は静止していると考えなければならない。つまり、回転運動に関しても、Fの作用点はFの向きと逆向きに動いている。しかし、これだけでは、運動方程式は解けない。次の二つの束縛条件が加わる。
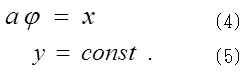以上で、初期条件以外の物理学的条件は(1)式~(5)式のなかにすべて組み込まれたことになる。一組の連立方程式をどのように解くかは、純粋に数学の問題であり、それは、方程式に登場している力の種類に制約されない。もともとのF やR が、束縛力であろうとなかろうと、運動方程式を座標で積分しようと、時間で積分しようと、数学的手法を自由に駆使して解けばよい。数学は厳密であるが自由である。
まず、（2）式と（5）式から導かれるのは、斜面に垂直方向の力の釣り合いであり、この場合、抗力Rは仕事をしない。残る（1）、（3）、（4）式を用いてx方向の運動をどう解くかは、いろんな解法が考えられるが、ここでは、F をいつ消去するか、そのタイミングが異なる二つの方法からエネルギー保存則を導いてみよう。
解法１：まず最初にFとφの二つを消去して解く。その結果、方程式の変数は円筒の重心座標xのみとなり、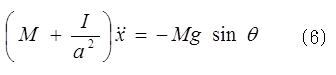
これから、xが時間tの関数として求められる。また（6）式を座標xで積分すれば、力学的エネルギーの保存則が導かれる。これが一般的な解法だが、この解法は、束縛力Fを最初に消去してしまうので、F の果たす役割が分りにくい。
解法2：そこで、Fを消去するまえに、（1）式を座標で積分すると、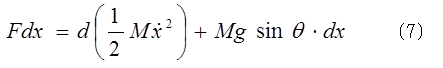
さらに円筒の重心位置の床からの高さをhとすると、次式になる。
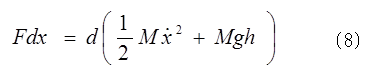次に円筒の回転の運動方程式（3）式をφで積分すると、
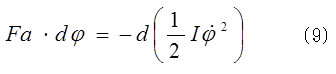（8）式と（9）式とでは、両式の左辺は等しく、（8）式は摩擦力が重心運動に正の仕事をすることを示し、（9）式は、同時に同じ摩擦力 が、回転運動に負の仕事をすることを示している。つまり、摩擦力は、回転運動からエネルギーを貰って、重心運動に正の仕事をしている。回転運動は負の仕事をされることによって、エネルギーを奪われているので、初期条件によって与えられていた回転運動のエネルギーがなくなると、摩擦力は、回転運動からエネルギーを貰えないので、重心運動に仕事をすることができず、円筒は一定の高さ以上には登れない。
円筒が最高点に達した後は、重心の移動方向も回転の向きも逆になるが、摩擦力の向きは変わらないので、今度は、摩擦力が、重心運動に負の仕事を、回転運動に正の仕事をしながら、斜面を転がり落ちる。Fを消去すれば、解法1と同じく力学的エネルギーの保存則が成り立つ。
解法2をカンダタが自転車で坂道を登る場合に適用すると、カンダタが足の筋力によってペダルを踏み、エネルギーが後輪の回転運動に補給されるので、カンダタは体力の続く限りどこまでも斜面を登ることができる。エネルギー源はカンダタ自身であるが、後輪に働く摩擦力が、後輪の回転に負の仕事をして、カンダタと自転車からなる系の重心運動に正の仕事をする。カンダタが自転車で坂道を登る場合と、円筒の問題を比較すると、カンダタというエネルギー源があるかないかの違いだけであり、どちらも摩擦力は回転運動に負の仕事をして重心運動に正の仕事をしている。
斜面を登る円筒の場合の解法1と解法2は両方とも正しい。ところが30年以上前に発表され話題となった論文Psuedowork and real workでは、いきなり、「束縛力は仕事をしない」という前提から議論が展開されている。この論文に惑わされてか、多くの物理教育関係者は、Fは斜面から受ける束縛力だから、その作用点は動かないので、 斜面から受ける静止摩擦力Fを重心の座標xで積分した量は、仕事の定義から、仕事ではないと主張する。しかし、円筒の運動を重心運動と回転運動に分解すれば、重心運動は質点の運動と考えることが出来るので、作用点は重心に他ならない。また、回転運動では重心は静止していると考えるので、Fが作るトルクの作用点も動いている。Fが重心運動にする仕事（8）式も、Fが回転運動にする負の仕事(9)式も通常の仕事と変わりはない。仕事と呼んでも、仕事として扱っても何の不都合も生じない。
束縛力は正味の仕事はできないが、運動を重心の運動と重心のまわりの運動（回転や変形）に分解すれば、束縛力も正と負、一対の仕事をすることができることを、（8）式と（9）式とが示している。束縛力と仕事についての、この考えは、人の体のように、エネルギーの発生源を含む系に対しては、極めて有用であろう。次に、蜘蛛の糸を登るとき、カンダタを質点系として、議論を展開してみよう。
3.質点系の力学
図2のようにn個の質点からなる質点系が、天井の一点oから伸びない糸によって吊るされている。oと糸で連結されている質点を質点1とし、座標の原点をoに選び、質点iの質量をmi、その位置ベクトルをｒiとする。さらに質点1が原点oから受ける力のベクトルをFとし、質点jが質点iに及ぼす力をfij(i＝jは除く)とする。
質点1に対する運動方程式は
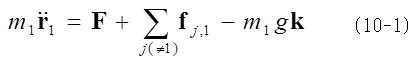その他の質点i(i=1でない）に対する運動方程式は、
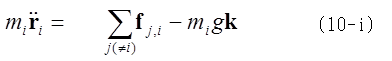ただし、kは鉛直上向きの単位ベクトルとする。ここでの束縛条件は
これで初期条件以外の、運動に関する物理的条件はすべてそろった。方程式を解く途中で、新たな束縛条件を付け加える必要はない。まず（11）式を時間で微分すると、ｒ1とその時間微分との内積が0あり、Fとｒ1とは平行であるから、Fと、ｒ1の時間微分との内積も0である。これは（11-1）のFが質点1の運動に対して仕事をしないことを示している。全ての（10-i)式において質点iの微小変位との内積をとると、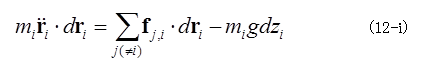
さらに、iで和をとると、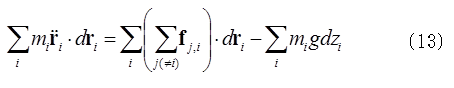
内力がした仕事をdWIN、質点系の運動エネルギーおよび位置エネルギーの増し分をそれぞれdKおよびdUとすれば、左辺はｄK、右辺第1項はdWINだから、（13）式は次式で表される。
ここで各質点の速度は質点系の重心の速度と重心から見た質点の速度の和であるから、つまり、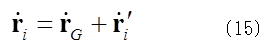
さらに質点系の質量をMとすると、質点系の運動エネルギーKは、
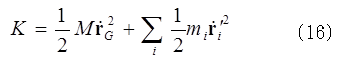（16）式の右辺第2項は重心の周りの運動エネルギーであり、これをK‘とすると、（14）式は、
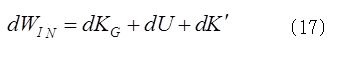もし、（17）式をカンダタが蜘蛛の糸を登る場合に適用すると、重心のまわりの回転運動は無視できるので、K‘は屈伸運動などの変形運動のエネルギーである。
（17）式は質点系の全エネルギーの増加分が筋力の仕事によるという当然の結果を示しているだけで、これだけでは張力が果たす役割が分からない。力Fの役割を見るために、（10-1）式+∑（10-i)式 とすると、内力はすべて打ち消し合い、かわりに、力Fが消えずに残る。つまり、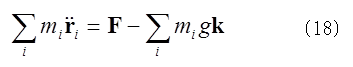
これはさらに、
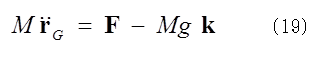（19）式は、質点系の運動から、重心の運動のみを取り出した方程式であり、重心に質点が存在しているとして、扱ってよいので、力の作用点は重心である。ただし、それは張力説に反対する人々とは意見が分かれるところである。（19）式を重心の座標で積分すると、
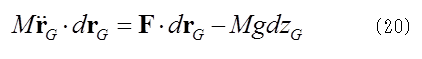右辺第1項は力Fが重心運動に対してした仕事だから、これをdWFとすると、(20)式は
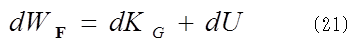（17）式と（21）式から、
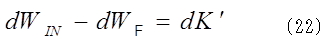（22）式は、内力が仕事をして、系の回転や変形運動にエネルギーを補給し、力F は、それらの運動に負の仕事をしていることを示している。一方、（21）式は、力Fが、負の仕事をして得たエネルギーによって、重心運動に仕事をしていることになる。また円筒の斜面登りの場合はdWIN=0であるから、（22）式は円筒の斜面登りの場合の（9）式に相当する。
張力説では、束縛力が重心運動に仕事をしていると考えるので、最初から、運動方程式（19）式をもとに議論を展開できるという利点がある。カンダタが蜘蛛の糸を登るとき、エネルギーを補給しているのは筋力であるが、重心運動に仕事をしたのは、張力だと考えることができる。
4.ブランコに乗ったカンダタ
ブランコを自分では振れずに、公園で母親に押してもらっていた幼児もやがて自分だけで上手に振れるようになる。母親に押してもらう場合は明らかに母親が仕事をしているが、自分で振る場合は、外力が働いていないのに何が仕事をするのだろうか。
まず、幼児が乗ったブランコを振り子に置き換えて考えてみよう。振り子の振れを増すには、公園の母親のように、振り子の振動に同期した周期的な力を外部から振り子に加えればよい。
振り子は水平方向に揺れるとともに上下方向にも揺れている。つまり、振り子には二つの振動が存在し、重りは水平方向に一回振れる間に上下方向にも２回振れている。
幼児を手助けしている母親は水平方向の振動に合わせて周期的な力を水平方向に加えているが、上下方向の振動に合わせて周期的な力を加えることはできないだろうか。
図3のように、滑車をとおして長さを変えることのできる振り子を考えてみよう。振り子の振動周期の半分の周期、つまり、振り子の上下動の周期に合わせて糸を引っ張ったり緩めたりすると、振り子の重りは図3のような振動数の比が１対２のリサージュ図形を描く。
通常、振り子の張力は重りの運動方向と常に垂直であるので、張力はおもりの運動に仕事はしないが、この場合は、糸の張力が、おもりの運動方向と直交していないので、今度は張力に仕事をさせることができる。
図3において、人の手が糸を引っ張り、おもりがＡ点からＢ点に向かうとき、糸の張力とおもりの運動方向がなす角は鋭角となるので糸の張力は振り子の運動に正の仕事をする。一方、糸を緩め、おもりがＢからＣに移動するとき、張力と運動方向は鈍角となるので、糸の張力は負の仕事をする。糸の張力は、糸を引くときが、緩めるときより大きいので、一周期に渡って張力がする仕事は正となり、振り子の振れは大きくなる。
蜘蛛の糸でできたブランコを自力で揺らしているカンダタもブランコの上で立ったり屈みこんだりすることによって、自分の重心の位置が図のような∞字のリサージュ図形を描くように変化させ、ブランコを吊るしている蜘蛛の糸の張力に仕事をさせているのである。
5．おわりに
運動を重心運動と回転や変形運動に分解して考えるとき、束縛力と仕事について、数学が我々に教えてくれることは、「束縛力は正味の仕事をしない」ということであり、「束縛力は一切仕事をしない」のではない。束縛力が仕事をしたと考えても不合理や不都合なことは何も生じない。それでも、張力説の「欠点」を強いてあげるなら、学生の予備知識のレベルによっては、無からエネルギーが生まれるかのような誤解を与えかねないことであろう。しかし、それさえ注意すれば、張力説の方が、筋力説よりも一層踏み込んだ説明が可能となる。
力学は、微積分や変分など数学的な手法を取り入れて発達してきたが、初等力学の教育においては、数式に頼らず、力学現象を直感的にやさしく説明することは、極めて大切なことである。しかし、一方では、数学的裏付けのないままに、直感と限られた経験だけで「束縛力は一切仕事をしない」としてしまっては、新しい発想の可能性を閉ざすことになるのではないだろうか。
1）後藤信行 ：日本物理発会誌71（2016）No.2,127
2）吉岡大二郎：日本物理学会誌71(2016)No.9,650
3）後藤信行 ： 同上
芥川文学「蜘蛛の糸」を巡る力学論争
力学
コメント