中心軸oのまわりに摩擦なしで自由回転できる円盤上に図のようなABCDの溝が掘られているとしよう。円盤が始めに静止していて、溝のなかのA点に静止していた一匹の虫が動きだし、溝のなかを、A→B→C→D→Aのように一周してA点に戻ってきたとしよう。
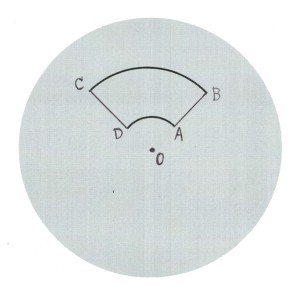 虫がA点からB点に向かって這うとき、虫は円盤に後ろ向きの力を与えるが、その力はo点のまわりの力のモーメントに寄与しないので円盤が回転することはない。しかし、虫がBからCに向かって這うと、円盤は時計回りに回転し、虫がC点に到着して止まると円盤の回転も止まるが、その間、円盤は右回りに一定の角度だけ回っている。
虫がA点からB点に向かって這うとき、虫は円盤に後ろ向きの力を与えるが、その力はo点のまわりの力のモーメントに寄与しないので円盤が回転することはない。しかし、虫がBからCに向かって這うと、円盤は時計回りに回転し、虫がC点に到着して止まると円盤の回転も止まるが、その間、円盤は右回りに一定の角度だけ回っている。
虫がCからDに向かって這うとき、円盤は回転しないが、DからAに向かって這うと、円盤は左回りに回転し、虫がA点で静止すると、円盤の回転も止まる。このときの左回りに回転した角度の大きさは、虫がBからCに向かうときに円盤が右回りに回転した角度より小さい。
虫は溝にそって1周してA点に戻って来たから、虫と円盤の系はもとの状態に戻るが、系は右回りに回転していることになり、外力働いていないのに、内力によってその向きを変えている。虫が円盤の上を這っている間も、虫と円盤からなる系の角運動量はゼロであり、これは猫の逆さ落としと同じである。
次に、角運動量の保存則をコリオリーの力から説明するのに、反時計まわりに自由回転している円盤のAB間を虫が往復する場合を考えよう。このとき虫がAからBに向かって這うと、今度は円盤が回転しているので、虫にはコリオリの力が進行方向に対して右向きに働き、虫が溝の壁を右向きに押すので、円盤の回転は遅くなる。逆に虫がBからAに向かって這うときは、コリオリの力によつて、円盤の回転は速くなる。つまり、円盤が回転している場合は、虫が中心から遠ざかると円盤の回転は遅くなり、中心に近づく速くなる。
円盤と虫からなる系の慣性モーメントは変化するが、角運動量は一定である。しかし、系の回転エネルギーは変化する。A→Bでは、遠心力が虫の運動に仕事をするので、その分、系の回転のエネルギーは減少し、B→Aでは、虫が遠心力に逆らって仕事をするので、回転エネルギーが増す。アイススケートのスピンで腕を屈伸して回転速度を変化させるのと同じである。 参考:福済寺の床
回転円盤上を這う虫
 回転運動
回転運動
コメント