ひまわり
再び、汽車に乗り、現在の妻子のもとに去っていく初老の男。それを無言で見送るかつての妻。汽車は朝靄の中を、汽笛を鳴らしてミラノの駅をゆっくりと加速しながら離れてゆく。ヴィットリオ・デ・シーカ監督の名作「ひまわり」のラストシーンである。この映画をこれまで何回見たことだろうか。戦争によって翻弄された二人の運命、何度見ても、最後の列車での別れが涙をさそう。
映画や歌謡曲に登場する列車は愛する男女を無情にも引き離していく。しかし、後ろ髪引かれる思いで去っていくのは列車のなかの主人公だけだろうか。走っている列車には、列車の走る方向と逆向きに動いている部分がある。列車には、別れを惜しむかのように、「行きつ止まりつ」しながら、さらには、「行きつ戻りつ」しながら、進んでいる部分が存在しているのである。答は車窓からの景色ではない。
畑もとぶとぶ家もとぶ
しかし、車窓からの景色も、動いていないはずの畑や家が後ろ向きに動いて見える。また、地上を走る車などの速さも、観測者が乗った列車の速さによっていろいろに見える。線路と道路が平行で、列車と車が同じ向きに走っているなら、列車から見える車の速度は、駅を発車した列車が速度を上げるにつれ、次第に遅くなり、やがて車は止まって見え、さらに列車が速度を上げると、車は後ろ向きに動いているように見える。
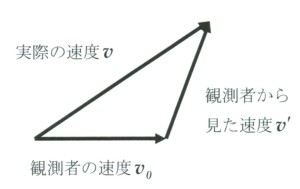
動いている観測者から見た速度は実際の速度から観測者の速度を引いたものとなるが、この関係は観測者の速度と対象物の実際の速度が同一方向でない時も成り立つ。ただ、その場合には左図のようにベクトルどうしの引き算となる。例えば、地上を速度v で走る車を、速度v0 で走る列車のなかから見た車の見かけの速度v´ はv から v0を引いたベクトルで表わされる。
実際の速度vから観測者の速度v0を引いたものが観測者から見た速度v´であるから、観測者から見た見かけの速度v´に観測者の速度v0を加えると実際の速度vが得られる。
列車の車輪
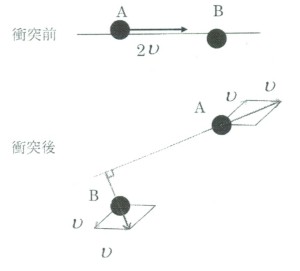
それで、今度は観測者が車に乗り、列車の線路と平行な道路を車で走り、列車を追いかけながら見てみよう。車の速度を上げると、列車の速度はだんだんと遅く見え、車が列車と同じ速度になると、列車の車両は止まって見える。このとき列車の車輪は、図の(a)のように、静止した中心のまわりを回転しているだけのように見えよう。実際の車輪の各部分の速度は、列車と一緒に運動する観測者から見た速度(a)に観測者の速度(b)を加えればよい。その結果、列車の車輪の各部分の速度は(c)のようになっていることがわかる。
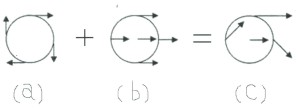
車輪が滑らずに転がっていれば、車輪の線路と接している点の速度は当然ゼロであるが、列車の速度の大きさをv とすれば、車輪の各部分のうち、最高点にきたときの速度は2v となる。上図は、右辺の車輪の転がり運動(c)が、重心の並進運動(b)と重心の周りの回転運動(a)に分解できると解釈することもできる。
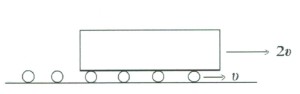
古代エジプト人は石を運ぶのにコロを用いたと考えられるが、物体をコロで動かすとき、物体はコロが動いた距離の二倍だけ移動する。コロが地面に対してL だけ移動すると、物体はコロに対してもさらにLだけ移動するからである。あるいは、物体はコロの最高点と接して動くため、コロの上に置かれた物体の速度は、コロの最高点の速度に等しいことからも理解できよう。
自転車の車輪は車体と一緒に動くが、コロで物体を運ぶ場合には、物体はコロの二倍の速さで動くため、コロは物体の後ろに次々と取り残されることになる。そのため、使用するコロの個数が少ないと、後ろに取り残されたコロを、次々と前方に運ばなければならない。
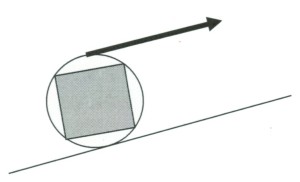
古代エジプトでは石を運ぶのに、コロの使用とともに、四角い石に木の枠をあてがい、円筒形にし、それに巻いたロープを引っ張って転がす方法も考案していたという。この場合には、石は、綱を引っ張った長さの半分の距離だけ移動することになる。当時、それに用いたと思われるクレードル(ゆりかご)の形をした木枠も発掘されている。
サイクロイド
列車の車輪には脱輪防止のためにフランジがつけられている。さらに車輪は円錐形に作られているため、例えば、列車が右にカーブするとき、遠心力によって車輪は線路に対して左に移動するため、左の車輪の回転半径が大きくなり、右の車輪の回転半径は小さくなる。こうして、列車は線路の上をスムーズにカーブしながら走ることができる。
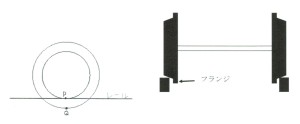
車輪上の、レールと接する一つの点をPとすると、列車が走るとき、P点の速度は、レールと接した瞬間はゼロであるが、車輪が半回転した後には列車の速度の2倍となる。つまり、P点は前述した、「行きつ止まりつ」しながら運動している部分ということになる。
列車が直線状のレールを走っているときのP点の運動の軌跡を考えてみよう。これは下図のようなサイクロイドとなる。このサイクロイド曲線には力学的にいろいろと興味ある性質が存在する。
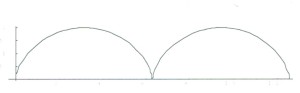
「重力場の中で、異なる高さの2定点を滑らかな曲線でつなぎ、高いほうの定点から物体を初速度ゼロですべり落としたとき、もう一方の定点まで到達するのに要する時間が最小となるのはどのような曲線か」という懸賞問題が出されたき、ニュートンはそれに匿名で応募したという。彼は変分法と呼ばれる数学的手法を考え出し、それをを用いて最速降下線を求め、その解がサイクロイド曲線となることを示したのである。つまり、図を上下逆にしたような曲線である。匿名での応募にもかかわらず、審査員には、その応募者は、ニュートン以外には考えられないと思ったという。
サイクロイド曲線を逆さにして任意の点から静かにすべり落とした場合、最下点に到達する時間は始めのスタート点に関係なく一定となる。つまり、最下点付近で振動させる時、周期は振幅に関係なく、一定となる。
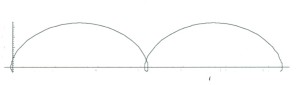
車輪が転がるとき、P点より、内側の点の軌跡をプロレート曲線、外側の点の軌跡をカーテート曲線とよび、両者の総称をトロコイド曲線という。例えばQ点の軌跡は下図のようになる。
それでは、P点より外側のフランジの部分はどのような運動をしているだろうか。その点Qが最下点に来たときは、列車と逆向きに運動し、車輪が半回転して、車輪の最上部にきたときは列車の速度の二倍を越える。つまり車輪のフランジの部分は「行きつ戻りつ」の運動を繰り返しているのである。
ガリレイの相対不変性
一定の速度で動く列車の窓に固定して写したビデオと地上に固定して写したビデオを比較してみよう。二つのビデオを区別するのは簡単である。車窓から写した映像には動くはずのない畑や家が動いて見えるからである。しかし、映像が物体の放物運動などの純粋に力学的現象のみしか映っていなければ、二つの映像のどちらが、地上からの映像で、どちらが車窓からのものであるか、判断することは不可能である。つまり、ある力学現象が静止系で起こりうるなら、それを、一定の速度で動く観測者から見た現象は、静止系でも起こりうるのである。あるいは、現象に関係しているすべての物体の速度に、任意の一定速度を加えた現象も現実に起こりうる。これをガリレイ変換に対する不変性とよぶ。
静止したビリヤードの球に他の球を直衝突させると、衝突した球が静止し、静止していた球が動き出す。衝突によって速度が他の球に移り変わるのはなぜだろうか。直衝突でない場合には、衝突後、両球とも動くが、衝突後の二球の運動方向はほぼ直角である。相対運動に対するガリレイ不変性を用いてビリヤードの球の衝突を考えてみよう。
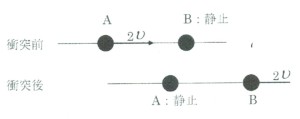
まず、二つの球の重心が静止した座標系から、球の衝突を見てみよう。互いに反対方向に同じ速さ で動いてきた質量の等しい二つの球、AとBが互いに正面衝突したとしよう。図のように、衝突前は、同一直線上を、左側のAは速さvで右方に運動し、右側のBは同じ速さで逆向きに動いていたとする。両者の衝突が、弾性衝突であれば、衝突後のAとBは互いに逆向きに速さvで遠ざかることは容易に想像できる。
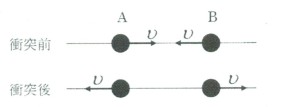
上の二つの図は同じ現象を異なる座標系から見たことになる。前者の座標系を重心系、後者を実験室系と名づけることにしよう。重心系では衝突の前後で、系の重心の位置は静止しているが、実験室系では系の重心は等速度運動をしている。両者は同じ現象を一方から他方へガリレイ変換したものと考えることができるが、いずれも衝突の前後で球A、Bが速度を交換することに変わりはない。さらに、この衝突では、エネルギーも運動量も衝突の前後で保存している。
もし、二つの球A、Bが粘土のような反発力のない材質で作られていれば、重心系では衝突後二つの球は合体して静止する。これを実験室系から見れば、静止している球Bに、球Aが2 vで衝突すると、衝突後は合体した2球が速さvで運動することになる。この場合、エネルギーは保存していないが、運動量は保存している。
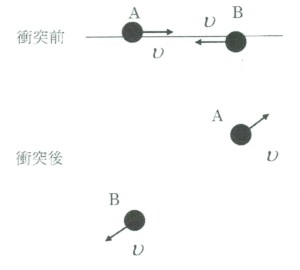
次に、図のような、質量の等しい二つの弾性球AとBの斜め衝突を重心系で考えよう。互いに同じ速さで接近する二球の中心の軌跡は平行であるが、同一直線上ではないとする。衝突前の系の運動量はゼロであるので、衝突後も系の運動量はゼロでなければならない。そのためには、衝突後の二球AとBは互いに反対方向に同じ速さで運動しなければならないが、斜め衝突なので、衝突後は衝突前の速度と平行にはならない。
この現象を衝突前のBと同じ速度で運動し続ける観測者から見ると、静止している球Bに球Aが衝突し、衝突後、二球は互いに直角、あるいは直角よりも小さな角度で離れていくことになる。並進の運動エネルギーが保存していれば、衝突後、二球は互いに直角方向に運動するが、衝突によって並進運動のエネルギーに損失があると、二球は衝突後、直角より小さい角度をなして遠ざかる。
これはまた次のように運動量保存則を用いて導くこともできる。速度v の球Aが、静止している同じ質量の球Bに衝突し、衝突後、A、Bの速度がそれぞれ、vA、vB になったとすると、運動量の保存則は
mv=mvA+mvB (1)
である。この両辺を2乗し、エネルギー保存則を用いると、
vA・vB>0 (2)
が成り立つ。つまり、弾性衝突であれば、 のうち、ひとつがゼロ、または両者が互いに直交するが、非弾性衝突の場合2球運動方向のなす角が直角より小さくなることを示している。
スウィングバイ
ボールを壁に投げつけると、跳ね返ってくるボールの速さは、投げつけた速さを超えることはできない。しかし、近づいてくる壁にボールを投げつければ、投げつけた速さより速く跳ね返ってくるだろう。逆に、遠ざかる壁に投げつければ、ボールはエネルギーを失い遅くなる。
もし、壁に垂直に投げつけ、衝突が弾性衝突であるとすれば、衝突後に跳ね返ってくるボールの速さは、投げつけた速さより、壁の速さの2倍だけ速くなる。これもガリレイ変換に対する不変性から明らかであろう。野球でボールがバットの芯に当たれば、打球は投手が投げた速さより速くなるのと同じことであるが、この当たり前の原理が宇宙空間に打ち上げられた宇宙船を加速するのにも用いられている。
静止した惑星に遠くから宇宙船が近づくと、宇宙船の運動の軌道は惑星を焦点とした双曲線となる。惑星が宇宙船に及ぼす場は保存場であるから、宇宙船の速さは惑星に近づくほど速くなるが、惑星の後ろ側を回って再び惑星から遠ざかるにつれ、宇宙船は遅くなり、十分離れたところでは宇宙船は最初の速さと同じ速さになる。宇宙船は静止した惑星の重力場によって運動の向きは変えるが、運動エネルギーは変わらない。
しかし、惑星が動いていると事情は異なってくる。動いている壁にボールを投げつけるときのように、宇宙船は惑星とエネルギーのやり取りをすることができる。これが宇宙船の運動エネルギーを増減すのに利用されるスウィングバイと呼ばれる方法である。

コメント