式F0(x,y)=0で表される閉曲線で囲まれる面積をSとし、変数tの1価連続関数の集合を、fn(t) (n=1,2.3・・・)とする。y→y-f1(x)と置き換えた式;F0(x,y-f1(x))を改めて、F1(x,y)とすると、式F1(x,y)=0で表される曲線も閉曲線になり、それは最初の閉曲線F0(x,y)=0をy方向にf1(x)だけずらした閉曲線だから、カヴァリエリの定理によって囲まれる領域の面積もSに等しい。次に、閉曲線F1(x,y)=0を今度はx方向にf2(y)だけずらした閉曲線はF1(x-f2(y),y)=0であり、これを改めてF2(x,y)=0とすると、その囲む面積もSである。このように、閉曲線を一価関数によつてy方向とx方向とに交互にずらしていくと閉曲線を表す項数は指数関数的に急激に増え閉曲線の形も複雑になる。しかし、囲まれる面積はSのままである。具体的な例として、fn(t)をnに関係なく、fn(t)=t2とし、最初の閉曲線F0(x,y)=0を単位円に選ぶと、次々に閉曲線を次のようにつくることができる。
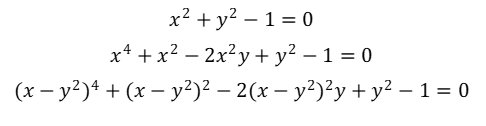
上記の第1式は単位円の式であるが、第一式のyにy-x2を代入したのが第2式である。さらに第2式のxに今度はx-y2を代入した式が第3式である。この操作を繰り返すと、Fn(x,y)=0は左辺の項数が指数関数的に急激に増え、その形も複雑になる。それにも関わらず、閉曲線Fn(x,y)=0が囲む領域の面積は単位円の面積に等しい。fn(t)をどう選ぶかでいくらでも複雑にすることができる。そのようにしてつくられた閉曲線の式からchatgptは面積を計算できるだろうか。
参考 カヴリエリの定理

コメント