1. 単一運動と複合運動
真空中で一定の高さから球を自由落下させると、落下するまでの時間は高さだけで決まる。この場合、球が回転しながら落下しても、それが落下時間に影響を及ぼすことはない。物体の自由落下や、自転しながら太陽のまわりを回る地球の運動のように物体の重心運動と回転運動とが同時に生じていても、二つの運動が連動していなければ、二つの運動は、それぞれが単一運動である。
しかし、球や円柱や円筒などが、回転軸を水平に保ちながら、斜面を転がり落ちる場合には、回転していない状態から運動が始まっても、重心運動が生じれば同時に回転運動も生じる。運動は斜面に沿った重心運動と重心のまわりの回転運動とが連動した複合運動となる。今度は二つの運動が連動しているため、同じ距離をころがり落ちても、ころがるのに要する時間は、球、円柱、円筒とで異なる[1]。さらに転がる物体に円対称性が存在しない場合には、滑らかに転がらず、おむすびころりんのように斜面と衝突を繰り返しながら転がり落ちるだろう。いずれの場合も斜面から受ける抗力によって重心運動と回転運動とが連動している。
2. 仕事の定義
高校物理教科書の力学の箇所や岩波書店の広辞苑には、物体に力が働いて物体が動いたとき、仕事は力と物体の変位との内積として定義されている。物体の位置は重心の位置で代表されるので、物体の変位とは重心の変位である。物体に働く力と物体の重心の変位との内積として定義されている仕事を仕事Aと呼ぶことにしよう。これに対し、岩波書店の理化学辞典には、系に働く力と、その力の作用点の変位の内積として定義されている。この仕事を仕事Bと呼ぶことにしよう。
高校教科書でも熱力学の箇所では、仕事は圧力Pと体積変化dVの積として定義されている。断面積Sのシリンダー内の圧力Pの気体をピストンに力Fを加えて、ピストンをdxだけ押し込むとき、P=F/S、dV=Sdxであるから、PdV=Fdxであり、高校教科書も熱力学での仕事は力と作用点の変位の積になり、理化学辞典に定義されている仕事Bと一致する。仕事Bはエネルギー保存則であり、力学でも運動方程式を解けば、物体全体の運動に対してした仕事として仕事Bが求まる。
仕事Aと仕事Bの違いは明確であり、力との内積の相手が重心の変位か力の作用点の変位かの違いだけである。教科書に定義されている仕事Aも、理化学辞典の仕事Bも、どちらも簡潔に記述されている。それに対し、発行年が比較的新しい培風館の物理学辞典では両者が混同されているため、冗長な記述になっていて、物体の変位なのか、作用点の変位なのかが釈然としない。
定義する意義は他と明確に区別することによって混乱を避けるためである。定義する段階で既に仕事Aと仕事Bとを混同させては定義する意味がない。仕事Aと仕事Bとを混同させても構わないのは運動が単一運動の場合だけである。二つの運動が連動した複合運動において両者を混同させては力学は混乱に陥る。
熱力学では系全体の並進運動や回転運動を考えないので、仕事Bのみで済むが、力学では、力が物体の重心運動にする仕事は仕事Aである。さらに、力が物体の回転運動にする仕事は、力のモーメントと回転角との変化量の積として定義される。これを仕事A’と呼ぶことにしよう。力のモーメントを一般化力、回転角を一般化座標と考えると、仕事A’は仕事Aと同類の仕事と考えられる。剛体の運動において、重心運動と回転運動とが連動していない場合は、仕事Aと仕事A’のどちらも仕事Bに等しくなるので、仕事は仕事Bだけで事足りるが、二つの仕事が連動している場合には、仕事Aも仕事A’も仕事Bに等しくはならない。ただし、両者の和は仕事Bになる。
抗力はその作用点は動かないので、仕事Bをすることはできないことは確かだが、物体の重心が動けば、力の作用点が動かなくても抗力は仕事Aをすることができる。また、物体が回転すれば、抗力は仕事A’をすることができる。力学はニュートンの運動法則がすべてである。その運動法則は、力の作用点が動くか動かないかで、力を区別してはいない。さらに、抗力が仕事Aや仕事A’をしても、二つの仕事の和をとれば、抗力の仕事は打ち消し合いエネルギー保存則に反しない。
3. 複合運動に対する正負同時一対の仕事
物体一般の重心運動に対する仕事は本来仕事Aであるが、重心運動が他の運動と連動していない場合は、重心の変位は力の作用点の変位と等しくなるので、その時の仕事は仕事Aでも仕事Bでも同じである。同様に回転運動に対する仕事も本来は仕事A’であるが、固定軸のまわりの回転運動や、回転運動が他の運動と連動していない場合には仕事A’でも仕事Bでも同じになる。
単一運動を扱う限りにおいては、仕事はすべて仕事Bで表すこともできるので、仕事Aや仕事A’の必要性を感じないが、球などが斜面を転がる運動のように、重心運動と回転運動とが抗力を介して連動する複合運動では、運動方程式は、重心運動と回転運動の二つの運動方程式からなる連立方程式になり、仕事Aや仕事A’が必要になる。連立方程式で表される運動方程式を数学を用いて解けば、球などの重心に働く重力は重心運動に対して正の仕事をするが、回転運動に対しては、力のモーメントをつくらないので直接には仕事をすることはできない。回転運動に仕事をする力は斜面から受ける抗力のみである。抗力のする仕事を否定しては、球などが斜面を転がるとき、回転のエネルギーがどのようにして得られるか、その仕組みが分からない。ころがり運動の運動方程式から導かれる結果は、重力が重心運動に仕事をし、抗力は重心運動に負の仕事をして、その分、回転運動に正の仕事をすることを示している。
4. 固定観念によるPseudoworkの誤謬
ニュートンの運動法則は、作用点が動くか動かないかで、力を区別していない。ころがり運動では運動法則に基づき運動方程式をつくれば、あとは数学的に抗力のする仕事がごく自然に導かれる。それにも関わらず、一部の物理教育関係者は、頑なまでに抗力の仕事に反対する。それにはアメリカで40年前に発表された論文[2]が影響しているようである。ころがり運動の場合、運動方程式から導かれる仕事は仕事Aと仕事A’だけであり、両者の和をとれば仕事Bになる。しかし、論文[2]は議論を運動方程式からはじめることなく、抗力はその作用点が動かないので仕事をする筈はないという先入観に囚われ、仕事Bを真の仕事とし、仕事Aを擬の仕事として議論を展開した結果、力学にはエネルギーに寄与しない擬の仕事が存在すると結論している。仕事Aと仕事A’の和である仕事Bに、さらに仕事Aを付け加えれば、二つの仕事Aと、一つの仕事A’とを組み合わせたことになる。個々の式は正しくても、コピペのように、ニュートン力学から導かれた数式を無理に継ぎ接ぎして組み合わせた結果、ギリシャ神話の双頭の怪獣キマイラになっている[3]。ニュートンの運動法則に則して運動方程式をつくり、数学を用いて解けば[4]、キマイラもロクロ首も現れることはない。
5. 日常の力学
物体の自由落下や物体が静止した状態から転がり落ちる運動では、そのエネルギー源は物体が初期条件に持っていた位置エネルギーであるが、自転車に乗って加速するときのエネルギー源は、乗っている人の足の筋力である。そのエネルギーがどのようにして、人を含めた自転車の重心運動に伝わるのだろうか。
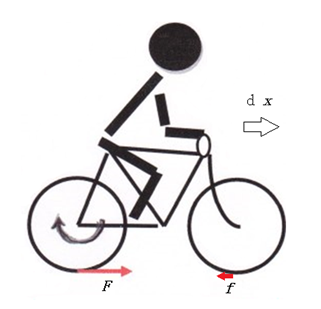
図1のように、人はペダルを踏むことによって後輪の回転運動に仕事をすると、後輪は地面から進行方向に抗力を受け、その抗力は後輪の回転運動に負の仕事をすると同時に、その分、自転車全体の重心運動に仕事をする。同時に前輪には後ろ向きの抗力fが働き、fは重心運動に負の仕事をし、前輪の右回りの回転運動に仕事をする。
次に図2のように、鉄棒にぶら下った人が、腕を縮めて懸垂する場合を考えてみよう。懸垂も、重力場の中での重心運動と腕の変形運動とからなる複合運動とみなすことができる。
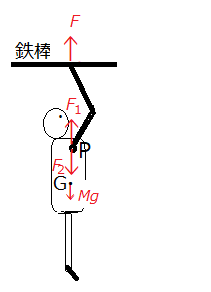
鉄棒から人の手の平が受ける上向きの抗力Fと同じ大きさで、向きが上向きおよび下向きの外力F1とF2が腕の付け根P点に働いていると仮定しても、F1とF2は打ち消し合うので運動に関係しない。F1とF2の作用点であるP点の変位は、腕が縮んだ長さ、つまり、重心の変位に等しい。つまり、人に働く力は重力の他に、作用点の動かない力Fと作用点が重心の変位に等しいF1とF2とが働いていることになる。そのうち、腕の両端に上向きと下向きに同じ強さで働くFとF2は、人が腕の筋力によって腕を縮めようとすると、その変形運動に逆らって負の仕事をする。残りのP点に上向きに働く力F1が重心運動に仕事Aをし、腕が縮んだ長さだけ人の重心を上に引き上げる。重力以外には、もともと存在する外力は作用点の動かない抗力Fだけだから、抗力Fは腕の変形運動に負の仕事をすると同時に重力場のなかの重心運動に正の仕事をしていることになる。
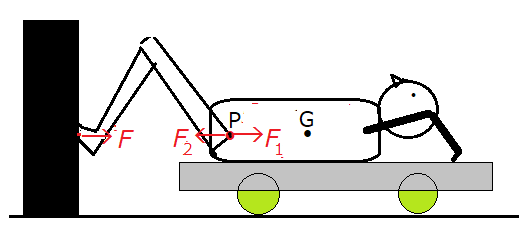
図3のように台車の上に人が仰向けに寝て足で壁を押す場合も、本質的には図2の懸垂と同じだが、壁が存在しなければ、足を伸ばしても重心Gは動かない。壁からの抗力がなければ、重心運動と変形運動とは連動しないからである。しかし、壁から抗力Fを受けると重心運動が生じる。その場合、懸垂の場合と同じく、今度は足の付け根のP点に、大きさがFと等しい仮想的な二つの外力、F1とF2が働いていると考えればよい。人が足の筋力によって足を伸ばそうとすると、FとF2とがその変形運動に負の仕事をし、F1がその分だけ、重心運動に仕事Aをする。図2でも図3でもP点の変位と重心の変位とが等しいことが重要である。
単一運動のみを扱うなら、仕事は仕事Bのみとしても構わない。しかし、日常の力学現象は単一運動より複合運動が圧倒的に多い。抗力のする仕事を否定し、抗力の仕事を含む可能性のある仕事Aや仕事A’の存在を否定し、仕事Bだけが唯一の仕事だとしたのでは、ほとんどの力学現象において、エネルギーがどのように配分されるか説明できない。図1~3のいずれの場合も、抗力のする仕事を否定しては、力学的エネルギーを供給したのは、人の筋力だという当たり前のことしか説明しかできない。力学的エネルギーの総量の出所を説明できても、それが複合運動にどのような仕組みによって、どう配分されるかが分からなければ、内訳が分からないドンブリ勘定の会計報告書のようなものであろう。
高校の力学では、抗力が仕事をする複合運動は扱わないので、仕事は仕事Bだけで、仕事Aも仕事A’も必要ではない。しかし、抗力は作用点が動かないという理由で抗力のする仕事を禁止しては、高校の力学は、複合運動への通路を閉ざされることになる。高校で、複合運動を教えなくても、そこへ通じる道を封鎖してはならない。Pseudoworkは、封鎖された仕事Aのバイパスにはなり得ない。
[2] Pseudowork and real work[Am.J.Phys.51(7),597-602,1983]
[3] 妖怪に牛耳られた力学教育

コメント