長崎発「トンデモ説」の主張
- 作用点が動かない外力である抗力も仕事をすることができる
- 抗力が仕事をしてもエネルギー保存則に反しない
- いかなる運動法則にも反することなく抗力も仕事をする
- 日常の多くの力学現象に抗力の仕事は必要不可欠である
- 但し、Pseudoworkの考えとは相容れない
動力源が系外に存在するとき
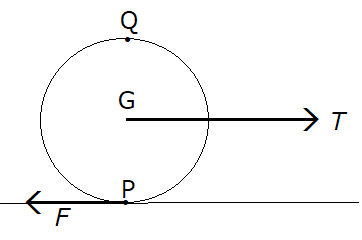
円柱の転がり運動を重心運動(並進運動)と重心のまわりの回転運動に分解する。M:円柱の質量、I:円柱の慣性モーメント、r:円柱の半径、v:重心運動の速度、ω:回転の角速度。
- 重心運動の運動方程式:
- T−F=M(dv/dt) (1)
- 回転運動の運動方程式:
- rF=I(dω/dt) (2)
転がり運動を分解すると各点の速度も図2のように分解され、各点に働く力も図3のように分解される。
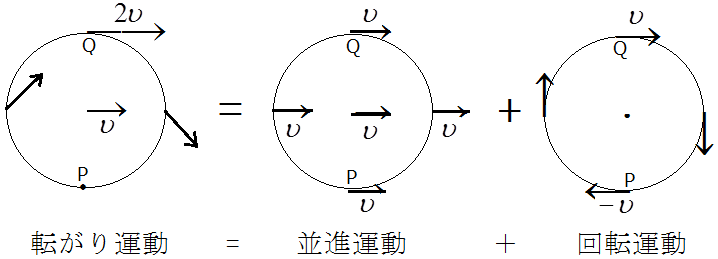
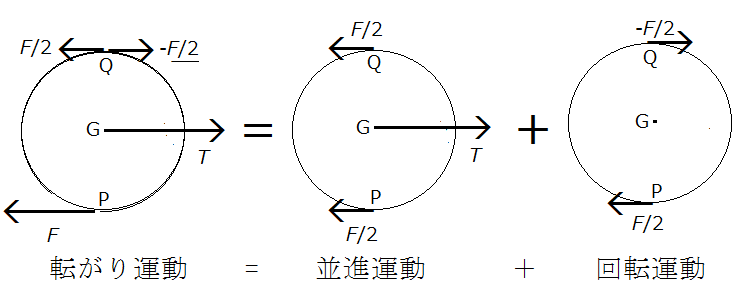
図2の速度の分解は明らかであろう。図3の転がり運動ではP点に働くFを2分割して、それぞれを重心運動と回転運動のP点に配分する。また、Q点には力は働いていないが互いに逆向きの力が働いていると仮定しても運動に影響しない。それを分解した二つの運動のQ点に配分する。図2と図3から転がり運動に対してFの作用点Pは動かないので、Fは転がり運動に対して仕事をしない。しかし、重心運動に対しても回転運動に対してもFの作用点は動いている。
なお、転がり運動の運動方程式は(1)と(2)からなる連立方程式になるが、二つの式からFを消去すると、P点を回転軸として固定した単一の回転運動となり、その場合のP点に働く抗力は回転軸を固定するために重心運動の遠心力と釣り合い、図1の転がり運動のFとは異なる。
動力源が系内に存在す場合
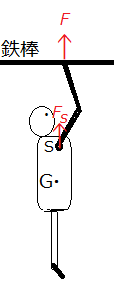
人が鉄棒で懸垂するとき、重心運動の方程式は、
F−Mg=Mα (3)
となるが、重心運動に仕事をするのはFだろうか。それとも肩の関節Sが腕の付け根から受ける上向きの力FSだろうか。
Fの作用点は動かないが、FSの作用点Sは上向きに動く。しかし、 FS が支えているのは全身の重さでなく、腕の重さを除く部分である。腕を除く部分に対して FS は外力になり、その仕事は FS と作用点Sの変位との積となり、 FS が仕事をすることに何も問題はない。しかし、 FS が引き上げているのは腕を除く部分である。
懸垂の場合、腕がエネルギーを供給する動力源となるので、その質量を無視することはできない。重心運動に仕事をするのは全体重を支えている鉄棒から受けるFでなければならない。
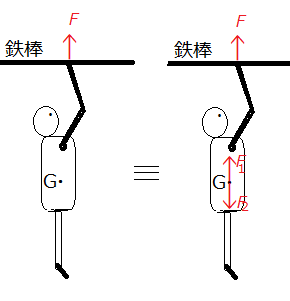
人全体の運動には、(3)で表される重心運動だけでなく、筋力による腕の変形運動が存在し、Fは二つの運動に関わっている。
抗力Fの役割を理解するには二つの運動の連立方程式を解かなければならないが、筋力による変形運動の方程式は力学の範疇ではないので、(3)の対となる変形運動の運動方程式は作れない。そこで、図5の右図のように 人の重心に大きさがFと等しいF1とF2を加えて考えてみよう。そのようにしても運動に影響しない。
ここで、FとF2を対として考えると、その一対の力は、筋力が腕を縮めようとするのを妨げる応力の役割をするが、重心運動には寄与しない。残る重心に働く力F1が重心運動に仕事をする。
重心運動と変形運動は抗力Fによって連動し、Fは腕の変形運動に負の仕事をするとともに、重心運動に対して正の仕事をして、重心を引き上げている。Fは人の全体運動においては抗力であり、その作用点は動かないが、転がり運動の(1)式のFも懸垂運動の(3)式のFも、重心運動を全体運動から分離した時点で、抗力ではなく重心に働く力に変化している考えるべきである。
長崎発「トンデモ説」と巷説「蜘蛛の糸」
腕を曲げるだけでなく、背中を丸め、腰や膝を曲げ、全身を縮めて懸垂をする場合もFは、全身の変形運動に負の仕事をして重心運動に正の仕事をする。ここで、これがもしかしたら、「蜘蛛の糸」の真相ではないかと、巷で囁かれている二つの説について考えてみよう。
①捏造説:お釈迦様は蜘蛛の巣の縦糸でなく、粘着性はあるが、切れやすい横糸のほうを垂らしため、カンダタは糸に絡まった。慈悲深いお釈迦様は身動きできなくなったカンダタを引き上げようとしたが、途中、蜘蛛の糸が切れてカンダタは元の地獄に堕ちた。
②悪人正機説:極楽から垂れ下がった蜘蛛の糸を自力で登ったカンダタは、途中、蜘蛛の糸が切れたにも関わらず、極楽に辿りついた。
二つの巷説の力学的な違いを説明しようとしたことが、長崎発「トンデモ説」の発端となったが、Fを蜘蛛の糸の張力とすれば、カンダタの重心運動の運動方程式は、いずれの場合も蜘蛛の糸が切れるまでは(3)式で表される。力学的エネルギーを供給したのは、①ではお釈迦様の筋力であり、②ではカンダタの筋力であるが、重心運動に仕事をしたのは、どちらも蜘蛛の糸の張力である。
また、①で、(お釈迦様+カンダタ)を一つの系とみなせば、エネルギーを供給したのは、お釈迦様の筋力だが、系の重心運動に仕事をしたのはお釈迦様の足に働く蓮池の淵からの抗力である。
作用点の動かない外力(抗力などの束縛力)が一切仕事をしないなら、蜘蛛の糸に絡まったカンダタと同じく身動きがとれなくなった高校の力学は極めて限定され、カンダタを質点として扱う①の場合だけにしか適用できなくなる。
しかし、抗力のする正と負の一対の仕事によって、重心運動とその他の運動とが連動した系においても、動力源が系外に存在していようと系内に存在していようと力学的エネルギーの移動が高校物理教科書の仕事の定義を変更することなく説明できる。

コメント