1.はじめに
力学において、速度や運動量など並進運動に関する物理量をベクトルで表すとき、そのベクトルの方向と向きは明らかであるが、角速度、角運動量など、回転運動に関する物理量では、そのベクトルの方向と向きを決めるのに左右の概念が用いられる。力学のみならず電磁気学まで含めて、一般にベクトルには極性ベクトルと軸性ベクトルとがあり、両者は空間反転に対してベクトルの向きが反転するか否かで、次のように定義されている。
極性ベクトルも軸性ベクトルも座標の回転に対しては同じ変換法則に従うが、空間反転に対して向きが反転するベクトルを極性ベクトル、向きが変わらないベクトルを軸性ベクトルまたは擬ベクトルという。
極性ベクトルと軸性ベクトルについて上記の定義をAとすると、これとは全く逆の記述をした論文 [安藤裕康:「軸性ベクトルについて」天球儀 第 112 巻 第 4 号 p.255(112-4_255.pdf (asj.or.jp)]もある。その論文の定義をBとすれば、定義Bでは、空間反転で向きが変わらないのが極性ベクトルであり、向きが反転するのが軸性ベクトルとある。なぜ、真逆の二つの定義が存在しうるのだろうか。
2.何を空間反転させるか
定義Aと定義Bとでは、空間反転する対象が異なっているようである。定義Aでは、現象を空間反転させるのに対し、定義Bでは、現象はそのままで、現象を見ている観測者を空間反転させている。つまり、定義Bでは観測者の左右の概念が反転するので極性ベクトルの向きは反転せず軸性ベクトルの向きのみが反転する。まず質点の直線運動と質点の円運動を例にして、二つの定義について考えてみよう。
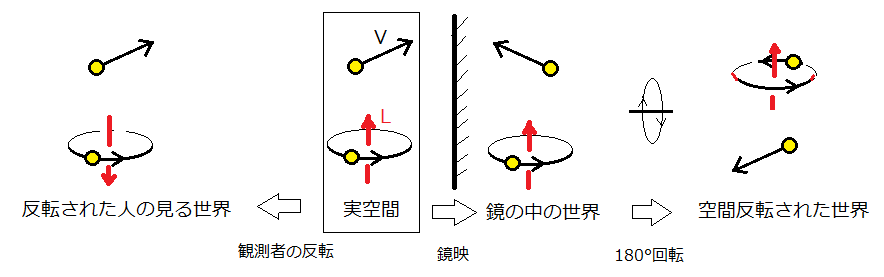
図1のように、実空間で、一つの質点は速度Vで直線運動し、もう一つの質点は角運動量Lで回転運動しているとしよう。実空間を鏡に映し、さらに鏡面に垂直な軸のまわりに180°回転させ、実空間を空間反転させると、質点の速度Vの向きは逆向きになり、質点の角速度や角運動量の向きは変化しない。よつて定義Aから、速度Vは極性ベクトルであり、角速度や角運動量は軸性ベクトルであることがわかる。
次に現象はそのままにして、観測者を空間反転させると、観測者の左右の概念が入れ替わり、観測者は自分の左手を右手と思い込み角運動量の向きを決める。その結果、速度の向きは変わらないが角運動量の向きが反転する。定義Bによって、向きが変わらない速度は極性ベクトルであり、向きの変わる角運動量は軸性ベクトルとなり、どちらの定義でも結果は一致する。
3.アンペールの法則
図1の質点を電荷と考えると、vが電流に相当し、Lは円電流のつくる磁界に相当する。電流Iと磁界Hに、定義Aと定義Bのどちらを適用しても、電流は極性ベクトル、磁界Hは軸性ベクトルになる。このことからアンペールの法則を空間反転させると電流の向きが反転し、磁界の向きは変化せず、図2のようになる。
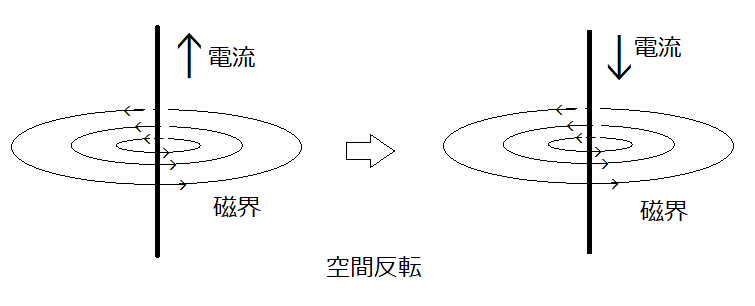
また、観測者の左右の概念を入れ替えると電流の向きは変わらず、磁界の向きが反転するので図3のようになる。
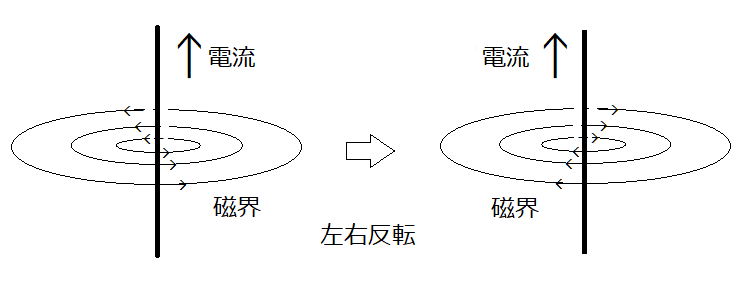
つまり、電磁気学でも二つの定義を用いた結果は一致する。
4.磁極の反転
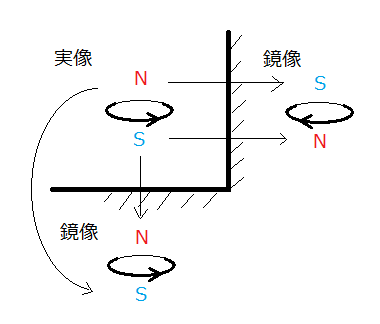
力学現象や電磁気現象を空間反転するには、鏡に映した鏡像を鏡に垂直な軸のまわりに180°の回転させればよいが、空間反転像は一義的に決まるのに対し、鏡像のその向きは、鏡をどう配置するかで異なる。
図4のように、円電流のつくる磁極を、配置の異なる二つの鏡に映すと、その鏡像の向きは二つの鏡で異なるが、N極の鏡像はS極になり、S極の鏡像はN極になることは鏡の配置に依存しない。これは鏡映や空間反転に対して、右手と左手が入れ替わるのと同じことである。
4.おわりに
力学と電磁気学における極性ベクトルと軸性ベクトルに関する定義Aと定義Bはどちらも正しく、どちらを採用するかは好みの問題である。しかし、空間反転させるのが現象なのか、それを観測している我々の左右の概念かを明確にしないと混乱してしまう。
アンペールの法則において電流と磁界の向きは、なぜ右ネジや右手を用いて決められるのだろうか。フレミングの左手の法則は、なぜ、右手だろうか。電磁気学現象において左右をすべて入れ替えれば、その法則は成り立たないだろうか? その答はコチラへ→自然界の対称性

コメント