江戸時代最後の元号を冠する有名私立大学の入試過去問であり、物体の運動に浮力の原理を組み合わせた次の問題は、疑問を持つことなく、その指示通りに考えていけば、正解とされる解答に辿りつくことは、さほど難しいことではない。しかし、解くには解けるが問題そのものに問題はないだろうか。

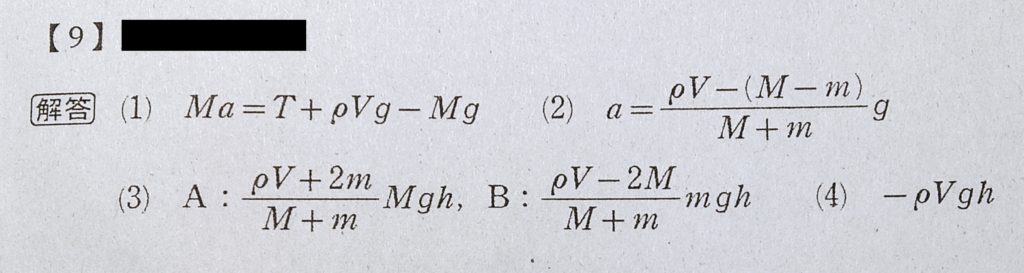
この問題には、次の二つの仮定がなされている。仮定①:液体がおもりAに及ぼす力としては浮力のみを考える。仮定②:液体の運動エネルギーは無視できるものとする。まず、仮定①のもとに、重りAとBの運動方程式をつくれば、それぞれ、次のように表させる。
Aの運動方程式:Mα=T+ρVg-Mg (1)の答 Bの運動方程式:mα=mg-T
あとは、数式の計算だけであり、二つの運動方程式から張力Tを消去すると、加速度αが求められ、それが(2)の答になっている。さらに計算を続ければ、(3)の答も次のようにして導き出せる。
おもりAが高さhだけ上昇し、その速度の大きさがvになった結果、重りAおよびBの力学的エネルギーが、それぞれ、ΔEAおよびΔEBだけ増加したとすると、それらは次のように表される。
ΔEA=(1/2)Mv2+Mgh ΔEB=(1/2)mv2-mgh
重りの速さが0からvになるまでの時間をtとして、重りはその間に、加速度αで等加速度運動をすると、 v =αt、h=(1/2)αt2となるから、両式から、tを消去すると、 v2=2αhとなる。これから、おもりA、Bの力学的エネルギーの変化は、ΔEA=Mh(α +g)、ΔEB=mh(α–g)となり、さらに(2)の答のαを代入すると、(3)の答が得られる。
液体の力学的エネルギーの変化を問う(4)では、仮定②より、液体については、その位置エネルギーの変化だけを考えればよいので、その答は簡単である。これで、この問題は完璧に解けたと思いたいが、一つの疑問が生じる。(3)で、重りAについては、運動エネルギーと位置エネルギーの両方を考慮しているのに、おもりAを囲んでいる液体については、運動エネルギーを無視してよいのだろうか。おもりAは液体を押しのけながら上方に等加速度で動くので、おもりAが動けば液体も動くはずである。
解答をみると、(3)の二つのおもりの力学的エネルギーの和に(4)の液体の力学的エネルギーの変化を加えると0になり、系全体の力学的エネルギーの保存則が成り立ち、一見、矛盾はないように思える。しかし、(4)では液体の運動エネルギーが無視されている。もし、運動エネルギーを無視しなければ、その分だけ、系全体のエネルギーが増加し、エネルギー保存則に反することになる。
問題作成の苦労は理解できるが、仮定①のもとに、液体の抵抗を入れずに、浮力だけを入れて、物体Aの運動方程式を(1)とすると、エネルギー保存則に矛盾するので、急遽、仮定②を設けて、液体の運動エネルギーを無視できると仮定するのは、適当に帳尻合わせをして粉飾決算をした放漫経営者の収支報告書のようなものではないだろうか。
球Aが液体中を有限な速さで動くなら、液体の運動も無視できない。液体の運動エネルギーが僅かだとしても、また、それが熱エネルギーに変わるとしても、系全体のエネルギーが増えることになり、熱力学第一法則に反する。エネルギー保存則に反するから液体の運動エネルギーを無視するというのは不自然である。不都合な結果を招いた原因は、仮定①のもとに物体Aの運動方程式をつくったためである。
①と②が仮定できるのは、液体の密度ρが限りなく0に近い極限であり、そのときは浮力も液体の抵抗も存在せず、真空中のアトウッドの装置になり、そのときの正解は、(1)Mα=T–Mg (2) α=-(M-m)g/(M+m) (3) A:2mMgh(M+m) B:‐2mMgh(M+m) (4) 0 となるが、もし、そのような解答をした受験生がいたとしたら、それも正解になるのだろうか。静力学や準静的な問題ではないのに、液体の及ぼす抵抗は無視するが、浮力は無視しないというのであれば受験生は混乱しよう。
受験生の中に、物理チャレンジ2019に応募した高校生はいなかっただろうか。そのときの第1チャレンジ実験課題は「水中を落下する物体の終端速度を求めてみよう」であった。何も考えず与えられた仮定①と②を疑うことなく受け入れれば、難なく解けるのに、問題の指示に疑問を持った物理チャレンジの高校生は、「正解」に到達できるだろうか。

コメント