図1のように、傾角θの斜面上に、球と円柱と円筒が静止した状態から、同時に滑ることなく、転がり始めると、どれが一番早く転がり落ちるだろうか。
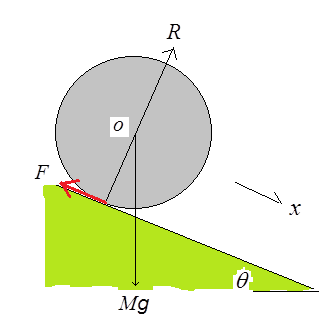
転がる回転体の質量をM、半径をr、慣性モーメントをI、斜面に平行で下向きにx軸を選び、物体が斜面から受ける抗力の、xの負の方向の成分をFとする。物体の並進運動および回転運動に対する運動方程式はそれぞれ、
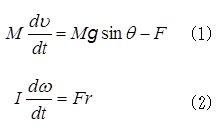
となる。ここで、vおよびωは、それぞれ、物体の並進運動の速度および物体の重心のまわりの回転の角速度であり、物体が滑らないためには次の条件、
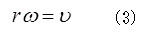
を満たさなければならない。vとωおよびFの三つを未知数とする(1)~(3)の連立方程式を解くと、転がり落ちる加速度および抗力Fはそれぞれ、
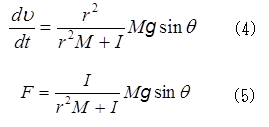
となることが分かる。ここで慣性モーメントをI=kMr2と表すと、
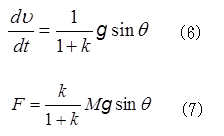
と表される。(6)式から、vはMやrに無関係であり、kが小さいほど、転がり落ちる加速度は大きくなる。kの値は、球では、2/5、円柱では、1/2、円筒では、1であるから、転がりレースの順位もその順になることが分かる。
抗力Fは転がり運動にどのような役割を果たしているだろうか。その役割を明らかにするために、もう一度(1)式と(2)式に戻って考えてみよう。重心が斜面に沿ってdxだけ変位したときの、物体の重心のまわりの回転角をdΘとすると、dΘ=dx/rとなる。(1)式の右辺は並進運動に働く外力だから、右辺とdxの積;(Mgsinθ-F)dxは、重力と抗力が並進運動にした仕事である。一方、(2)式の右辺;Frは重心のまわりの力のモーメントであるから、それとdΘの積;FrdΘはFdxに等しくなるが、それは抗力Fが回転運動にした仕事である。つまり、重力は並進運動に仕事Mgsinθdxをするが、回転運動には直接仕事をしない。それに対し、抗力Fは並進運動に負の仕事-Fdxをし、回転運動に正の仕事Fdxをしていることが分かる。
重力が並進運動にMgsinθdxの仕事をするにも関わらず、並進運動のエネルギーは、まるまるそれだけ増えることはない。抗力Fは作用点が動かないため、回転体の運動にエネルギーを供給できないが、並進運動と回転運動の両方に負の仕事と正の仕事をすることによって、重力の仕事によって回転体が得るエネルギーを並進運動と回転運動に再配分する役目をしている。もし、球、円柱、円筒の三者の質量が同じであれば、重力のする仕事はどれも等しいが、三者でkの値が異なるので、Fも異なり、並進運動に配分されるエネルギーも回転運動に配分されるエネルギーも三者で異なることになる。
この問題は運動方程式から始めなくてもエネルギー保存則からも説明できよう。つまり、「重力がした仕事=並進の運動エネルギー+回転の運動エネルギー」であり、落下距離が同じなら、左辺は同じであるので、回転の運動エネルギーに分配されるエネルギーが小さいほど、並進運動のエネルギーは大きくなる。しかし、エネルギーが二つの運動にどのような比で配分されるかは、並進運動のエネルギーは、なぜ、(1/2)Mv2なのか、回転運動のエネルギーは、なぜ、(1/2)Iω2かを知らなければならないが、それはエネルギー保存則からだけでは分からない。並進運動の運動方程式(1)および回転運動の運動方程式(2)を、それぞれ、重心座標xおよび回転角Θで積分して初めて分かることである。
円柱と円筒が斜面を転げ落ちる速さを競争させる実験は科学イベントでよく行われるが、両者の半径を同じものを用いると、円柱のほうが円筒より重いので速く転げ落ちるとの誤解与えかねない。異なる半径の円柱や円筒を準備して、半径や質量に関係なく、円柱のほうが速く転げ落ちることを示すことが大事であろう。

コメント