無色の正六面体の六つの面に、指定された異なる6色、例えば、黒、白、赤、紫、黄、緑を、それぞれ割り当てて塗るとき、異なる正六面体はいくつ、できるだろうか。一見、難しそうだが順序立てて考えればそれほどでもない。
まず、立方体の一つの面を黒色で塗ってみよう。どの面を黒く塗っても同じだから、立方体は1種類である。次に、黒い面に平行な反対側の面を白く塗っても立方体は1種類のままである。さらに、残る4面のうち、相対する二つの面を赤と紫に塗っても立方体は1種類のままである。
この時点で色が塗られていない面は相対する一組の2面だけとなったが、これに黄と緑に塗れば、作業は完了するが、どちらの面を黄で塗るかで、二種類の立方体ができる。それを確かめるために、黒、赤、黄の三つの面が見える側から立方体を見ると、黒、赤、黄が時計回りに配置する場合と反時計まわりの場合がある。他の三つの面は見えないが決まっているので、立方体の種類は二種類であることがわかる。
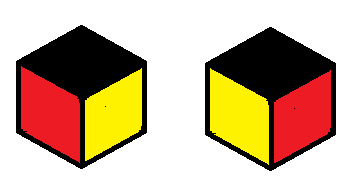
黒と白、赤と紫、黄と緑のように、三つのペアを固定して、ペアの2色を立方体の相対する面に、振り当てるという規則にしたがって色塗りすれば、2種類の立方体しかできない。
これと同類の問題がT大学の大学院の入試問題に出題されている。サイコロには立方体の各面に1から6までの数字が割り当てられているが、通常のサイコロは相対する二面の数字の和が7になるように、1と6、2と5、3と4とがそれぞれ相対する面になるように作られている。数字の向きを考えなければ、正六面体の色塗りの問題とまったく同じとなる。サイコロが規則通りに作られていればサイコロにも2種類しかない。
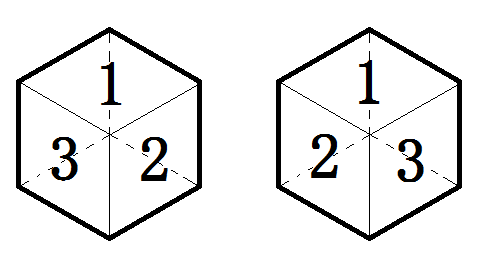
それでは、規則に縛られず、自由に六つの面に六つの色や、1から6までの数を振り分ける場合の数はどうなるだろうか。6色または、1~6までの6個の数を、三つのペアに分ける場合の数は15通りあり、それぞれに対して2通りの正6面体が存在するので、答は30通りとなる。色を塗り分けた場合も数を振り分けた場合も30通りの正6面体ができる。ただし、数を割り当てる場合、書かれている数の向きは問題にしないとする。
ここで、少々横道にそれるが、プラトンの正多面体について考えてみよう。五つの正多面体、すなわち、正4面体、正6面体、正8面体、正12面体、正20面体のうち、正6面体と正8面体、および正12面体と正20面体は双対の関係にある。双対の関係にある正多面体では、頂点の数と面の数を入れ替えると、相手の正多面体になる。正4面体は、相手が存在せず自己双対である。
正6面体の面を色分けするのは、それと双対の正8面体の6個の頂点を色分けするのと同じである。正6面体の六つの面の色をスケッチするのは難しいが、正八面体の六つの頂点の色を描くのは易しい。黒と白、赤と紫、黄と緑を三つのペアにして、それぞれのペアを、正8面体の中心に対して対称な二つの頂点に振り分けたとき、図3の右図になったとすれば、それを鏡に映した左図も条件を満たす図形である。
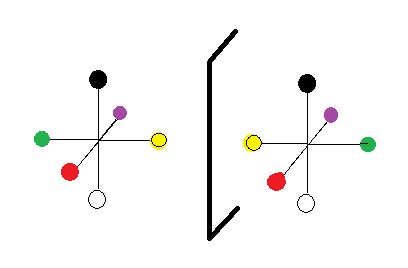
図3のようにもとの図形と鏡に映した図形がとが異なるとき、キラルな図形とよぶ。6色を3つのペアにして、それぞれのペアを正六面体の相対する2面に割り当てたとき、互いに鏡像関係な2種類の正6面体ができる。これは座標系に右手系と左手系とが存在するのと同じである。図1も図2も図3も実は皆同じことを意味している。
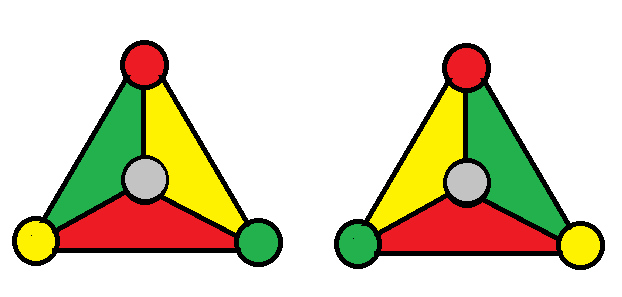
ついでに図4のように、正4面体の面を与えられた4色、赤、黄、緑、灰色で塗り分ける場合を考えてよう。正4面体は自己双対だから、4つの面を色分けすることは、それぞれの面に対応している4つの頂点を色分けするのと同じである。灰色に塗った面を下にして正4面体を台の上に置き、三つの側面を赤黄緑で塗る方法は、上から見て、赤黄緑の面、あるいは赤黄緑の頂点が、時計まわりに並ぶ右図と反時計まわりになる左図の二通りが存在する。つまり、正4面体を異なる4色で塗った場合、二種類の正4面体が存在する。
これは立体化学の問題でもあり、一個の炭素原子に付いている、四つの原子または原子団が異なるとき、その分子には光学的異性体が存在することを意味する。ただし、原子団にも炭素原子が含まれる場合には必ずしも光学的異性体が存在するとは限らない。
数学は面白い学問であるが、さらに、それを他の学問に応用するとさらに面白くなろう。
参考:自然界の対称性

コメント