高校の物理教科書には、仕事は次のように定義されている。
「物理では、物体に力を加えて、力の向きに物体を移動させたとき、力が仕事をしたという。物体に一定の大きさF[N]の力を加え、力の向きに距離s[m]移動させたとき、力が物体にした仕事Wは次のように定められる。W=Fs (仕事[J]=力の大きさ[N]×移動距離[m])」第一学習社「基礎物理」
他の出版社の高校の物理教科書、大学初年次の物理教科書、岩波書店の広辞苑も、さらにブルタニカ百科事典でも同様な定義である。
それに対し、岩波書店から出版されている理化学辞典は、仕事を次のように定義している。
「力学系に力 が作用し作用点がdsだけ変位するとき、スカラー積(F,ds)を、その力が力学系になした仕事という。」
高校の物理教科書での仕事の定義を定義A、理化学辞典の定義を定義Bと呼ぶことにしよう。床や道路から受ける抗力や固定点から垂らされた糸の張力などの作用点が動かない力も、定義Aでは、物体が動けば仕事をすることができるが、定義Bでは仕事をすることはできないことになる。
二つの定義は、どちらかが間違っているのだろうか。それについて、物理関係者の大多数の考えは、定義Bが、唯一、仕事の正しい定義であり、定義Aは、仕事の対象を質点に限定したときの定義だという。しかし、それなら、定義Aでの物体は、質点と書くべきである。質点という用語は高校教科書にもすでに使用されている。
概念を明確に区別するための定義が、物体と質点とを混同させているとすれば、しかも、それが物理学への入門としての高校の物理教科書のなかで放置されているとすれば、物理教育にとって由々しき事態であり、教科書の執筆者や、それを文部省時代から検定してきた文部科学省の歴代の多くの関係者は、チコちゃんに叱られる程度では済まされぬ。
古くから高校の物理教科書に採用されている定義Aは、仕事の対象を質点に限定したときの仕事の定義ではなく、仕事の対象を、物体一般の、しかし、その並進運動に限定したときの仕事の定義である。それを示すために、いくつかの例を示そう。まずは図1のような円柱のころがり運動を考える。
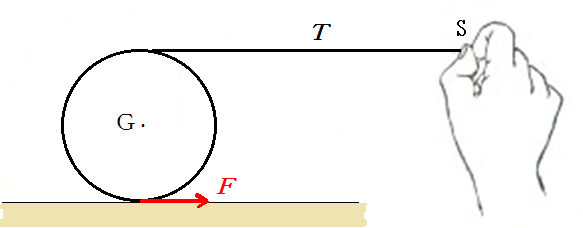
円柱に糸を巻き付け、水平な台上を滑らずに転がす場合、糸の張力をTとし、また円柱が台との接点において台から受ける水平抗力(静止摩擦力)をF とする。円柱の転がり運動において、重心がdx だけ変位すると、力T の作用点の変位は2dx であり、F の作用点の変位は0である。よつて、定義Bから、円柱の転がり運動になされた仕事は2Tdxとなり、仕事と円柱のエネルギーの関係式は
2Tdx =ころがり運動の力学的エネルギーの増分 (1)
となる。ここで、道路からの水平抗力Fは(1)式には現れないが、Fが仕事に果たしている役割を明らかにするために、図1の転がり運動を二つの運動に分離してみよう。
一般に、剛体の運動は並進運動と重心のまわりの回転運動の和として分離して考えることができる。図1の円柱の転がり運動も図2のように分離できる。
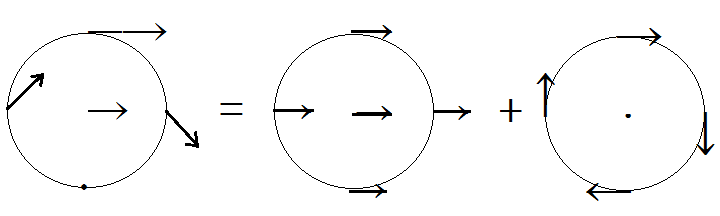
並進運動では、円柱のすべての点の速度は重心の速度に等しい。つまり、並進運動では、T の作用点もFの作用点も、その変位は重心の変位dx に等しいので、並進運動になされた仕事は、定義A、定義Bに関わらず、(T+F)dx である。よって、並進運動における仕事とエネルギーとの関係式は
(T+F)dx=並進運動のエネルギー増分 (2)
となる。アメリカで発表された論文Pseudowork and real work (Am.J.Phys.51(7),July1983) に頻繁に見られる は重心の変位であるとともに、全体運動から分離された並進運動に働いている力の作用点の変位でもある。
一方、全体運動から分離された回転運動では、重心の変位は変位せず、T の作用点の変位はdxであるが、Fの作用点の変位は-dxであるから、この場合も、定義Bから回転運動になされた仕事は(T-F)dxである。よつて、回転運動に対する仕事とエネルギーの関係式は
(T-F)dx=回転運動のエネルギーの増分 (3)
となる。Fの作用点は円柱の全体運動である転がり運動に対しては動かないが、運動を分離したとき、Fの作用点は並進運動に対しては、Fの向きにdxだけ動き、回転運動に対しては-dxだけ動いていることになる。よつて、(2)と(3)に示すように、Fは並進運動に正の仕事をし、同時に回転運動に負の仕事をしていることが分かる。(2)式と(3)式を加えると(1)式に等しくなる。
ここで(2)式の左辺は、抗力Fを含む外力の和と重心の変位との積であり、それが右辺の円柱の並進運動のエネルギー増分に等しいので、高校物理教科書の仕事の定義、つまり定義Aと一致する。教科書に記述されている定義Aが物体の並進運動に対する仕事であれば、定義Aは定義Bと矛盾しない。つまり、定義Aは、仕事の対象を質点に限定した場合の定義ではなく、物体一般に対する、しかし、その並進運動に限定した定義である。
図1の円柱の転がり運動では、動力源が系外に存在するが、その場合には、(1)式のみを仕事としても、(2)と(3)をそれぞれ分離した運動にする仕事としても、どちらで考えるかは好みの問題に過ぎないが、動力源が系のなかに含まれるときは、運動を分離して考える方が遥かに分かりやすい。動力源が系内に存在する場合も、力学的エネルギーは全て動力源が生み出しているが、定義Bにおける力は外力であり、定義Bは、系内に存在する動力源が系自身の運動にする仕事を想定していない。
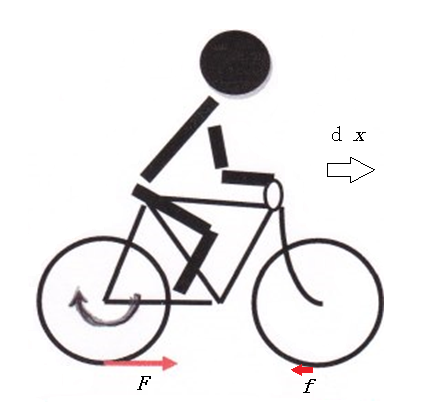
例えば、図3のように、人が自転車に乗って走る運動も、動力源の人と自転車からなる系の並進運動と系の変形運動に分離できる。この場合、重心の周りの回転運動は存在しない。人の足の筋力が後輪の回転運動に仕事をし、道路からの摩擦力Fは後輪の回転運動に負の仕事をし、同時に、系の並進運動に正の仕事をする。その結果、並進運動が生じると、前輪に摩擦力fが生じ、f は並進運動に負の仕事をすると同時に前輪の回転運動に正の仕事をする。これをすべて筋力のする仕事として片付けると、ドンブリ勘定になり、エネルギーの流れの詳細が分からない。運動を分離して考えるとき、定義Aによる仕事は必要不可欠となる。
円柱の転がり運動も自転車の運動も、水平抗力の作用点は全体運動に対しては変位しないが、全体運動を二つの運動に分離したとき、分離された二つの運動では、水平抗力の作用点は互いに逆向きに変位することを示している。これは垂直抗力が働く場合も同様である。
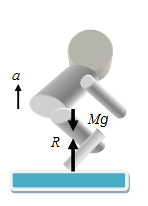
図4のように、人が床の上、床から垂直抗力Rを受けて立ち上がる場合を考えよう。人の立ち上がり運動も並進運動と変形運動とに分離できる。全体運動に対して動かない抗力Rの作用点も、分離された並進運動や変形運動では上向きに動くことになる。並進運動では床と接触している足の裏も重心とともに動くからである。その微小変位をdyとすると、抗力Rが人の並進運動にした仕事はRdyである。これは重力場のなかで質量Mの剛体をdyだけ持ち上げる場合の仕事と同じであるから、Rdyは、人を剛体と考えたときの、運動エネルギーと位置エネルギーの和の増し分に等しい。一方、変形運動では、人の重心は動かず、抗力の作用点は、並進運動とは逆に-dy変位するので、抗力Rは変形運動に-Rdyの仕事をする。内部の動力源である筋力が変形運動にする仕事をdWとすれば、変形運動になにされる仕事はdW-Rdyである。筋力は系の変形運動に仕事をするが、抗力Rは筋力の仕事によって生じた変形運動に負の仕事をし、重力場のなかの並進運動に正の仕事をしている。図4における垂直抗力の役目も図1や図3における水平抗力の役目と全く同じである。
図4の運動で人を上半身と下半身に分けると、上半身は下半身から受ける力によって持ち上げられるので、下半身の筋力が上半身の重心運動に仕事をしていることになるが、下半身も質量が存在するので、下半身の筋力は人全体の重心を持ち上げることにはならない。
無重力空間では、最初静止していた宇宙飛行士が、他に触れることなく、いくら手足を動かしても宇宙飛行士に並進運動は生じない。その場合、変形運動のエネルギーは飛行士の体内で熱エネルギーとして散逸するだけである。しかし、飛行士が宇宙船の壁などに触れ、そこから抗力を受ければ、抗力は飛行士の変形運動に負の仕事をし、同時に飛行士の並進運動に正の仕事をするため、並進運動にエネルギーが生じる。
アメリカで提唱され、それ以後、40年近くに亘って、物体一般の並進運動にする仕事は、力の作用点が動かないので?仕事に似て仕事ではなく、偽物の仕事だとしてきたpseudowork仮説に引導を渡すときがきたようである。全体運動に対しては作用点の動かない力として働く抗力も、全体運動から分離された並進運動では、抗力の作用点も重心と同じ速度で動いていることを忘れてはならない。

コメント