学歴ロンダリングとの蔭口も聞くが、目標を目指すのに途中のルートは関係なかろう。35年間の大学教員生活のなかで、新しい研究分野を求めて他大学の大学院受験を希望する学生はいつもいた。しかし、地方大学から中央の大学の大学院を受験するのは、かなりのハンディがある。それでも敢えて、他大学の大学院を希望する学生と一緒に物理と数学の過去問を解いたものである。ずいぶん時間が経ち、かなり忘れてしまったが、その頃を思い出しながら、退職後の脳活のため、昔のプリントを探しだし、シリーズで紹介しよう。
問 下図の五角形ABCDEは正五角形である。五角形FGHIJおよび三角形AIHの面積は、それぞれ、正五角形ABCDEの面積の何倍かを求めよ。(T大学大学院過去問)
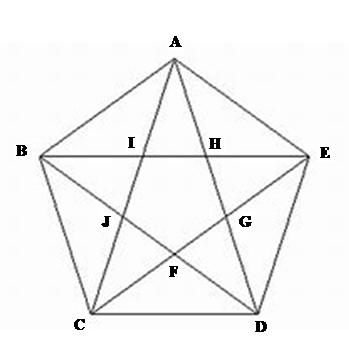
解説 三つの二等辺三角形、⊿ACD、⊿CDG、⊿DGFは相似である。CD、およびACの長さを、それぞれ1およびkとすれば、DGの長さは1/k、GFの長さは1/ である。また、⊿GAC も二等辺三角形であるからAGの長さは1である。k=AD=AG+GD=1+1/kとなる。よって、
-k-1=0となり、kは黄金比であることが分かる。内部の正五角形の辺の長さは、正五角形ABCDEの辺の長さの 1/
倍であるから、面積は 1/
倍 となる。
=(
-k-1)(
+k+2)+3k+2=3k+2。よつて、内部の正五角形の面積は、外部の正五角形の面積の1/(3k+2)倍。
正五角形ABCDEの面積=正五角形FGHIJの面積+5個の⊿ABJの面積に等しい。ABCDEの面積を1、二等辺三角形AIHの面積をsとすると、⊿ABJの面積は、s であるから、1=1/(3k+2) +5
s から、sを黄金比kで表すことができる。
この問題は正五角形のなかに黄金比が隠れていることに気づけばたやすく解けよう。他大学の学生には難しくても、長崎の学生なら、この問題、簡単に解かんば! 長崎市の市章は五芒星なんだから。


コメント