一般常識と力学の常識
生徒 「先生!質問があります。自転車に乗って水平な道路上を加速しながら走るとき、仕事をするのは、車輪が道路から受ける摩擦力、つまり、水平抗力だと考えてようでしょうか。」
教師 「いやいや、それは違うな。仕事をするのは自転車に乗ってペダルを踏んでいる人の筋力だよ。」
生徒 「でも、自転車に働いている外力は、車輪が道路から受ける水平抗力しかありません。」
教師 「垂直抗力であれ、水平抗力であれ、抗力は、その作用点が動かないので仕事をすることはできないよ。」
生徒 「しかし、筋力は自転車と人からなる系にとって、内力ですから系の並進運動には仕事をすることはできないと思いますが。」
教師 「抗力が仕事をしてくれるなら、人は疲れないじゃないか。日常経験に照らしても抗力が仕事をしないのは明らかではないか。」
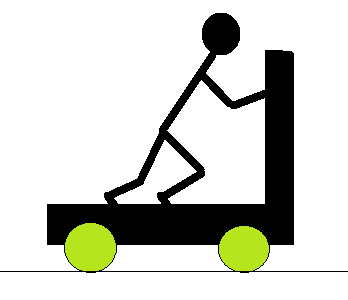
生徒 「しかし、内力が並進運動に仕事をしないのも日常経験から明らかだと思います。左図のように、台車の上で台車を押しても、人と台車からなる系の重心は動きません。」
教師 「台車では、人の筋力は台車の車輪の回転運動には伝わらないが、自転車では筋力がペダルとチェーンを通して後輪を回転させているではないか。」
生徒 「自転車では、後輪の回転に対して、確かに人の筋力が仕事をしていますが、道路からの抗力がなければ、台車の場合と同じく、系の重心は動きません。
教師 「自転車のエネルギー源は人の筋力以外ないではないか。
生徒 「エネルギー源は筋力ですが、道路からの抗力がないと、ペダルをいくら踏んでも後輪が回転するだけで、系の並進運動にはエネルギーが補給されません。
教師 「抗力がなければ、筋力派後輪の回転運動のみに仕事をするが、抗力があれば、筋力は後輪の回転運動と並進運動の両方に仕事をすることができるではないか。」
生徒 「抗力があるとき、後輪の回転運動のエネルギーが並進運動に伝わるためには、抗力のする仕事を考えなければならないと思います。
教師 「それは、抗力があれば、筋力は後輪の回転運動と並進運動の両方に仕事をすることができるということと同じではないか。」
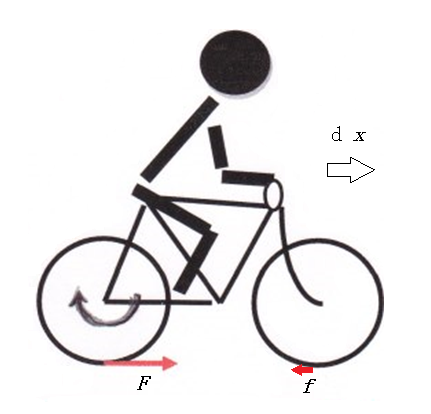
生徒 「筋力によって後輪に補給されたエネルギーが、抗力によってどのようにして伝わるかが重要だと思います。そこに触れずに、後輪の回転運動にも並進運動にも、筋力が仕事をすると考えてはドンブリ勘定となり、抗力の役目が分からなくなります。筋力が後輪の回転運動に仕事をして後輪が回転すると、後輪には道路からの前向きの抗力Fが働きますが、それは後輪に、回転とは逆回りのトルクとして作用します。つまり、抗力Fは後輪に負の仕事をすることになりますが、同時にFは並進運動に正の仕事をします。さらに並進運動が生じれば、今度は前輪に後ろ向きの抗力fが働き、fは並進運動に負の仕事をし、前輪の回転運動に正の仕事をします。仕事を段階的に考えることによって、筋力から後輪の回転運動へ、そして並進運動へさらに前輪の回転運動へと、エネルギーの流れが明確になるのではないでしょうか。
仕事の定義
教師 「確かにそれはいい考えだが、抗力派もともと仕事とは無縁の静力学において、力のつり合いを説明するために導入された概念だから、抗力が仕事をするという考えは、一般に受け入れられるのは難しいと思うけどな。
生徒 「抗力は静力学だけでなく動力学でも重要だとおもいます。道路からの水平抗力がなければ、自転車だけでなく人も歩けません。」
教師 「歩く人も自転車も、抗力のする仕事によってエネルギーを得るのではなく、抗力の力積から運動量を得て動くと考えるべきだ。仕事をするのは筋力ではないか。」
生徒 「力学の基本は運動方程式です。並進運動の運動量もエネルギーも、並進運動の運動方程式から導かれるべきです。運動量は抗力の力積で、エネルギーは運動方程式に現れない筋力というのでは、「木に竹を接ぐ」ことにならないでしょうか。」
教師 「作用点の動かない抗力が仕事をすることになると、ニュートン以来の仕事の定義を変更しなければならないことになる。」
生徒 「いえ、そのような大げさなことではないと思います。仕事の定義を変更する必要はありません。高校の物理の教科書には、仕事は、物体に働く力と、力が働いた結果、物体が移動した距離との内積と書かれています。抗力が仕事をしても、いかなる力学の法則にも反しないし、現行の教科書の仕事の定義にも反しません。」
教師 「高校の教科書は、物体が質点の場合、あるいは質点とみなせる場合に限定していると考えるべきだ。物体や系一般に対する仕事の定義は理化学辞典に記載されているように、力と、力が作用している作用点の移動距離との内積だ。しかし、理化学辞典の定義は初心者には難しいので、教科書では易しく書いているのだ」
生徒 「もし、そうだとすると、質点とみなせない物体、例えば回転を伴う剛体の力学を学ぶには、高校生は教科書だけでは不十分で、理化学辞典を読まなければならないことになります。理化学辞典の記述が高校生にとって難しすぎるとは思えません。それに難しく記述しようと、易しく記述しようと、言葉を定義する意義は、他と明確に区別することによって、無用な混乱を避けるためです。定義文のなかの「物体」を、物体一般でなく、質点に限定しているとか、「物体の移動距離」を、本当は「作用点の移動距離」の意味だというのでは議論は成り立ちません。これは力学以前の問題ではないでしょうか。高校の教科書は分かり易くかかれていますが、いい加減には書かれていないと思います。」
教師 「それでは教科書の仕事の定義が正しく、理化学辞典が間違いだというのか。
力学と熱力学

生徒 「いえ、教科書も理化学辞典も正しいと思います。例えば左図のような円柱の転がり運動を考えてみます。運動方程式は、並進運動(重心運動)と重心の周りの回転運動の方程式に分解して考えることができます。どちらの運動方程式にも作用点の移動距離なる量は現れません。この場合の円柱の状態変数は重心の座標と回転角であり、その状態変数を変化を引き起こす作用は、力と力のモーメントです。重心運動にする仕事は力と重心の移動距離との積であり、回転運動にする仕事は力のモーメントと回転角の変化との積です。どちらも作用の強さと、作用を受けた結果、状態変数の変化量との積です。系になされたすべての仕事を合計した結果は、外力と作用点の移動距離との積になりますが、力学ではそれぞれの運動に足しての仕事が定義されているので理化学辞典の定義は必ずしも必要ではありません。
教師 「高校の物理でもバネにする仕事は力と作用点の移動距離の積ではないか。」
教師 「理化学辞典の仕事が必要なのはどんな場合だ。」
生徒 「運動を分解して考えることのできない複雑な系では系全体にする仕事として理化学辞典の仕事が必要になるでしょう。それと、エネルギー保存則を基本原理とする熱力学では理化学辞典で定義された仕事が必要不可欠となります。高校の教科書でも、熱と温度の章では、仕事は圧力と体積変化との積として定義されています。熱力学では圧力は系が外部から受ける作用であり、その作用に応答する状態変数が系の体積です。しかし、力学も熱力学も、仕事とは、外部からの力や力のモーメント、そして圧力などの作用と、それに応答する、重心位置や回転角、体積などの状態変数の変化量の積という点では同じではないでしょうか。
教師 「従来の仕事の定義を変更する必要はないということか。
生徒 「そうです。しかし、抗力が仕事をしないという先入観は捨てて頂かなければなりません。抗力は正味の仕事はしませんが、仕事をする場合は、常に、正と負の仕事を同時にすることになります。
教師 「そうか、君の考えは理解できたよ。君の粘り強さには脱帽だ。しかし、抗力説を広めるには相当な抵抗があるだろうな。頑張りたまえ。
生徒 「本当は主体性もなく、いつも長いものに巻かれている小心者ですが、2300年の時を超えて出会った孟先生の言葉に後押しされ、ない勇気を無理矢理絞り出し、日頃、疑問に思っていたことを質問させて頂きました。有難うございました。
― 自らかえりみてなおくんば、千万人と雖も吾往かん ― 孟子

コメント