大学院入試過去問より
1モルの理想気体を作業物質とする系を考える。内部エネルギーUは温度Tのみの関数であり、また、状態方程式は圧力P、体積V、および温度Tを用いてPV=RTと表わされる。ただし、Rは気体定数である。なお、系に流入する熱量をδQ、系が外部に対して行う仕事をδWとすると、熱力学第一法則はdU=δQ-δWと表わされる。この時の系のエントロピー変化をdSとすると、熱力学第二法則はδQ/≦dSと表わされ、可逆過程では等号が成り立つ。これらを前提として、以下の問に答えよ。
A.図1のように、1モルの理想気体を入れたピストンを温度Tの熱浴に浸して温度を一定に保つ。ピストンを準静的に動かして気体の体積をV1からV2に変化させる過程(等温過程)を考える。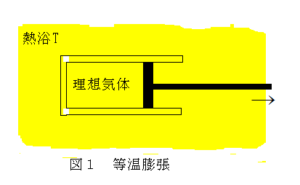
問A-1.この過程で系に流入する熱量を求めよ。
解:理想気体の内部エネルギーは温度のみの関数であるから等温過程ではdU=0だから、熱力学第一法則より、dQ=dW=∫1→2PdV=RT∫1→2(1/V)dV=RTlog(V2/V1)
問A-2.問A-1の結果を用いて、この過程に伴うエントロピーSの変化を求めよ。
解:準静的変化であるから、エントロピーの生成はなく、系のエントロピーの増加は熱浴から流入した分のみであるから、dS=δQ/T=Rlog(V2/V1)
B.図2aのように、断熱壁で囲まれた体積一定の容器に仕切りを入れ、体積V1の領域に温度T、圧力Pの理想気体1モルを入れ、体積V2の領域を真空にする。この状態から仕切りを取り去り、V1+V2の領域に気体を自由膨張させる過程を考える。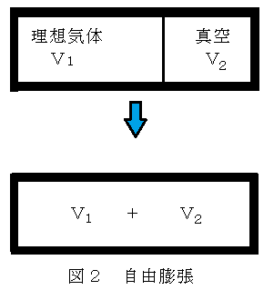
問B-1.この過程では気体の温度が変わらない。その理由を50字程度で答えよ。
解;断熱変化であるから、δQ=0、系は仕事をしていないのでδW=0、よつてdU=0である。UはTのみの関数であるうえに一定であるから、Tは一定となる。
問B-2.この過程に伴う気体のエントロピー変化を求めよ。
解:エントロピーは状態量であるから、始状態と終状態のエントロピーの差は、S(T,V1+V2)-S(T,V1)=Rlog((V1+V2)/V1)
問B-3.この過程は可逆過程か、不可逆過程か、理由を含めて50字程度で答えよ。
解:δQ=0にも関わらず、dS>0である。系の中でエントロピーが発生しているので、不可逆過程である。
AとBのどちらも気体のエントロピーは増えるが、Aでの増し分は、熱浴からの熱の流入に伴うエントロピーであり、熱浴とピストンの気体を一つの系と考えると、系全体ではエントロピーの増減はない。一方Bでの増し分は自由膨張によって発生したエントロピーである。熱力学の基本的な問題だが、最初の前文のなかに、ほとんどヒントが書かれているので、仕事が計算でき、エントロピーが状態量であることを理解していれば、確実に解ける問題であろう。
等温膨張と自由膨張のエントロピー
 大学院入試過去問
大学院入試過去問
コメント