 このページは旧版です。数式が見にくいので改定しました。改訂版にお移りください→コチラです。
このページは旧版です。数式が見にくいので改定しました。改訂版にお移りください→コチラです。
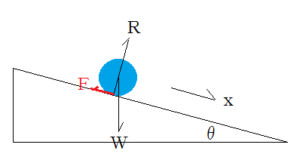
図のような傾斜角θの斜面を、球と円柱と円筒が、静止状態から同時に滑ることなく転がる場合、三つの物体のどれが一番早く転がるかを考えよう。斜面に平行に右向きに重心の座標xを選び、物体の右回りの回転角をφとしよう。物体には図のように、鉛直下向きに物体の重さW、斜面と垂直に抗力R、斜面と平行で進行方向と逆向きに摩擦力Fが働く。この場合、物体は斜面上を滑らないので、Fは動摩擦力でなく静止摩擦力である。物体の質量をM、半径をa、慣性モーメントをIとすると、重心のx方向の運動方程式、y方向の運動方程式、回転の運動方程式、および滑らないという束縛条件は次の(1)、(2)、(3)、(4)のように表わすことができる。
Mxtt=Mgsinθ-F (1)
0 =R-Mgcosθ (2)
Iφtt=aF (3)
aφ=x (4)
(2)式から垂直抗力Rが求められ、(1)、(3)、(4)を解くと、重心運動の加速度xtt、回転運動の角加速度φttおよび摩擦力Fは
xtt=gsinθ/(1+k) (5)
φtt=gsinθ/[a(1+k)] (6)
F=[k/(1+k)]Mgsinθ (7)
のように求められ、どれも、それぞれ一定値となる。ただし、I=ka2Mとしている。kは、物体が、球、円柱、および円筒の場合によって、それぞれ、2/5、1/2および1となる。よつて、(5)式から、転がる加速度は、球では、(5/7)gsinθとなり、円柱では、(2/3)gsinθ、そして円筒では(1/2)gsinθとなる。球、円柱、円筒を斜面の同じ高さから同時に転がせば、kの小さい順、つまり、球、円柱、円筒の順に床に達することが分かる。kが大ききほど遅くなるのは、kが大きいほど多くのエネルギーが回転運動に費やされなければならないからである。もし、斜面が完全に滑らかで摩擦がなければ、物体は回転せずに斜面滑るので、その場合の加速度はgsinθとなり、転がる場合よりも大きくなる。
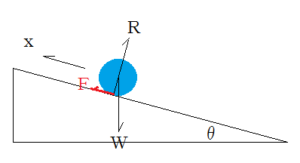
また、左図のように、物体が斜面を転がりながら登る場合、転がりの初速が同じなら、物体が登り得る高さは、kが大きいほど高くなる。
最後に、蛇足ながら、円柱と円筒が斜面を転げ落ちる速さを競争させる実験は科学イベントでよく行われるが、両者の半径を同じにしておくと、円柱のほうが円筒より重いので速く転げ落ちるとの誤解与えかねない。異なる半径の円柱や円筒を準備して、半径や質量に関係なく、円柱のほうが速く転げ落ちることを示すべきであろう。

コメント