中学の理科の授業で、レンズによる結像など、初めて幾何光学を習ったとき、球面凹面鏡の焦点距離は球面半径の半分であると教えられたが、その理由は教えてもらえなかったような気がする。そこで、凹面鏡の焦点距離について考えてみた。
球面凹面鏡
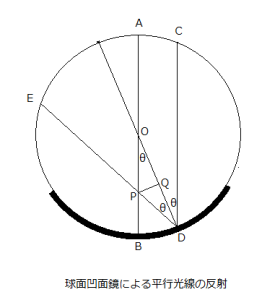
まずは、中学時代に分からなかった球面凹面鏡の焦点距離を平面幾何学によって導いてみよう。左の図のように、半径rの球面の中心Oを通る光線ABと、ABと平行な光線CDの反射光DEとの交点をPとし、さらに、PからDOに下した垂線の足をQとしよう。図から三角形PODは二等辺三角形であるから、OQの長さはr/2となり、BP=r-r/(2cosθ)となる。これから、θ→0の極限では、BP=r/2となる。つまり、近軸光線に対して、球面凹面鏡の焦点距離BPの長さは確かに球面半径の半分であることが分かる。しかし、平行光線が光軸から離れていくと、PはBに近づき、θ=π/3になると、PはBに重なる。これで中学時代の疑問は解けたが、近軸光線から外れても焦点が変わらない凹面鏡はあるだろうか。
放物凹面鏡
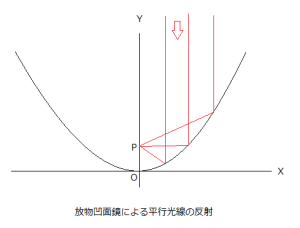
今度は高校数学の微分の知識が必要だが、球面の代わりに、左図のように光線が放物面鏡の光軸に平行に二入射した場合を考えよう。放物線の式をy=x2/4p、入射光線をx=aとすると、光線は放物線上の点(a,a2/4p)において反射の法則にしたがって反射される。この点における放物線の接線の傾き角をθとすると、反射光線の傾き角は(2θ-π/2)となる。よつて反射光線の式は
y-a2/4p=tan(2θ-π/2)(x-a)
となる。tanθ=a/(2p)だから接線の式は
y-a2/4p=(a2-4p2)(x-a)/(4ap)となり、これは、y=(a2-4p2)x+pとなる。この直線はaの値に関わらず、y軸上の点(0,p)を通る。つまり、放物凹面鏡では光軸に平行に入射した光は反射されると、すべて点(0,p)に集まる。衛星放送の受信アンテナは放物凹面鏡になっていて、光軸を静止衛星の方向に向けて取り付ける。
円と放物線
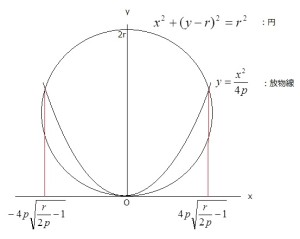
これも高校程度の数学だが、左図の円と放物線の二式からyを消去すると、xの4次方程式が得られる。図から明らかなように、r>2pのときは、この方程式の解は、正の解と負の解と、x=0(二重解)を持ち、r=2pになると、解x=0は4重解となり、r<2pでは実数解は、二重解のx=0のみとなり、他の二つの解は複素解となる。これは、r=2pの場合には、x=0の近傍では、放物線は円で近似でき、逆に、円は放物線で近似できることを意味している。
一般の平面曲線に対しても、狭い領域であれば、曲線の一部を円周として近似できる。今度は大学程度の数学となるが、それを次に示そう。
曲率と曲率半径
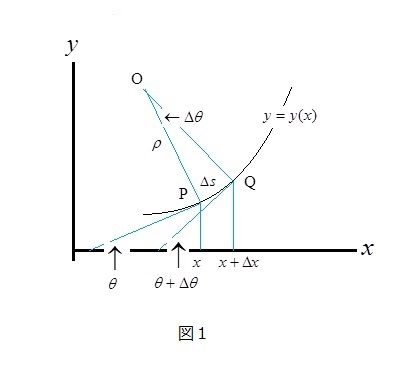



よつて、焦点距離がpの放物線、つまり、4py=x2の頂点における曲率半径を求めれば、その値は2pとなることが分かる。逆に半径rで中心の座標が(0,r)の円を放物線4py=x2で近似すれば、p=r/2となる。これで、中学時代の凹面鏡の焦点距離についての疑問は完全に解けた!
球面凹面鏡の焦点距離
 未分類
未分類
コメント