1. ヨーヨーの転がり運動
理工系の学生なら、大学の初年次に習うが、図1のような初等力学の演習問題を考えてみよう。水平な台上で、ヨーヨーの軸に巻きつけた糸を引っ張り、ヨーヨーを台上で滑ることなく転がす問題である。
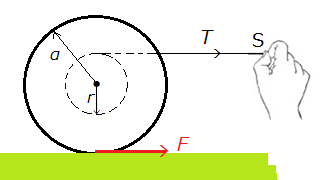
ヨーヨーの質量をM、中心軸のまわりの慣性モーメントをI、半径をα
、糸を巻き付けるヨーヨー内部の軸の半径をrとする。最初、静止していたヨーヨーの糸を引っ張ると、ヨーヨーは台上を滑ることなく転がり始めた。この問題をニュートン力学が導くままに数学を用いて解いてみよう。
2. ヨーヨーの運動方程式
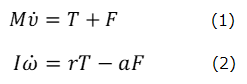
糸の張力をT、ヨーヨーが水平台から受ける水平抗力をF、ヨーヨーの重心速度の大きさをv、回転の角速度をωとする。ただし、水平抗力Fの向きは右向きを正とし、水平抗力が左向きに働く場合は、Fの値を負とする。ヨーヨーの運動方程式は、(1)式と(2)式からなる連立方程式になる。(1)は並進運動、(2)は回転運動の運動方程式であるが、Tが与えられると、未知数は、v
とω
、それにFの、三つになるが、ヨーヨーが滑らないためには、αω=v が成り立つので、未知数はv (またはω)とFの2つになり、(1)と(2)からなる二元連立方程式を解くことができる。
3. 運動量とエネルギー
ニュートン力学では運動に関する物理量は、運動方程式から導かれるので、暗記する必要は一切ない。並進運動は、運動量と並進運動のエネルギーを持ち、回転運動にも角運動量と回転のエネルギーが存在するが、それらがどのように表されるかも、すべて運動方程式から数学的に導かれる。
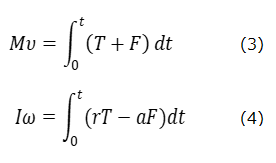
運動方程式(1)および(2)を時間tで積分すると、ヨーヨーの運動量および角運動量はそれぞれ、(3)式および(4)式になる。並進と回転の二つの運動は、さらに運動のエネルギーを持つが、それも、それぞれの運動方程式から導かれる。エネルギーを求めるには、今度は(1)式および(2)式の両辺に、それぞれ、vおよびωをかけたあと、時間で積分すれば、並進運動のエネルギー、回転運動のエネルギーは、それぞれ、次の(5)式および(6)式になる。
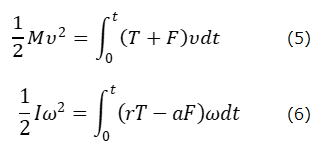
4. 力とその作用点の変位
(1)と(2)の運動方程式に現れる外力は、TとF
の二つだが、ヨーヨーが滑らなければ、水平抗力Fは台から受ける静止摩擦力であるから、その作用点は動かない。一方、Tの作用点は図1のS点であるから、dt時間での、その変位は(v+rωdtである。しかし、ニュートン力学は、力をその作用点の変位の有無によって区別していない。並進運動に対する(5)式は、dt時間内に、Tは仕事Tvdtをし、作用点の動かない水平抗力FもFvdtの仕事をしていることを示している。vdtは作用点の変位ではなく、ヨーヨーの重心の変位である。抗力Fは作用点が動かないのになぜ仕事をすることができるのだろうか。当然の疑問ではあるが、(6)式を見ればその理由が分かる。 ヨーヨーが滑らない条件、αω=vから、(6)式は、
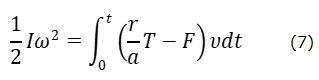
となる。つまり、抗力Fは並進運動に仕事をすると同時に、それと逆符号の仕事を回転運動にしている。(5)式と(7)式を加えると、Fのする仕事は消え
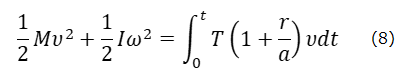
となる。(8)の右辺の積分のなかの(1+r/α)vは糸の張力の作用点Sの速度であり、(8)式は、ヨーヨーの全体運動、つまり転がり運動に対して、Tがする仕事は、Tとその作用点の変位との内積であり、エネルギー保存則が成り立っていることを示している。全体運動に対して仕事をするのは、作用点が動くTだけであるが、並進運動に対しては、TもFも仕事をし、そのときの仕事は、どちらも力とヨーヨーの重心の変位との内積である。
5. おわりに
抗力はその作用点が動かないので、一切仕事をしないと考えたい気持ちは理解できるが、それでは、ニュートン力学から導かれる(5)式や(6)式と矛盾する。約40年前にアメリカで発表されたpseudoworkの考えは、力学の仕事を熱力学や物性論の仕事と取り違えている。それ以後、今日までの40年間、力学における仕事についての議論が、時代錯誤の宗教裁判に変わってしまったようである。力学の仕事に対する混乱した議論が、ニュートン力学に基づいた正常な科学的な議論に一日も早く戻ることを期待して、この小文をブログに公開したい。

コメント