抗力は作用点が動かないので、外部から力学的エネルギーを系に供給することはできないが、系の二つの運動形態に正と負の仕事を同時にすることができるという趣旨の論文を日本物理教育学会の会誌に、再三再四に亘って投稿してきたが、今だ掲載してもらえない。抗力のする仕事を、辛抱強くホームページなどで主張し続ける他なさそうである。ニュートン力学を素直に受け入れれば、揉めるにも揉めようがないと思えるが、会誌編集委員会と筆者のどちらかが、抜き差しならぬドツボにはまっていることだけは確かなようである。
動力源が系の外部に存在する場合
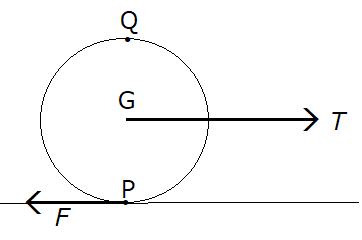
半径r、慣性モーメントIの円柱の重心に、図1のように、水平方向の力Tを加えて水平面上を右方向に転がすとき、円柱の接点Pが水平面から左方向に受ける水平抗力(静止摩擦力)をFとすると、円柱の運動方程式は、並進運動と回転運動の連立方程式として次のように表される。
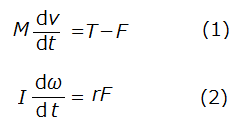
ここで、vは並進運動の速度、ωは回転運動の角速度である。円柱が滑らずに転がるには、v=rωでなければならない。円柱の転がり運動に関する情報、つまり、①円柱の運動量、②円柱の角運動量、③円柱の並進運動のエネルギー、④円柱の回転運動のエネルギー、⑤円柱の力学的エネルギーは、すべて、(1)と(2)の連立方程式から数学的に導かれなければならない。
①および②を求めるには(1)式および(2)式を時間tで積分すれば、それぞれ、Mv=(T-F)の力積、および、Iω=Fの力積のモーメント、となる。③および④は(1)式および(2)式に、それぞれ、vおよびωを乗じたあと、tで積分すれば、それぞれ、Mv2/2=(T-F)のした仕事、および、Iω2/2=Fのした仕事、となる。そして、③と④とを加え合わせれば⑤が求められる。以上は初等力学の常識だと思っていたが、そうでもないらしい。
日本物理教育学会の会誌編集委員会によれば、①と②を運動方程式から求めることは問題ないが、仕事をすることができる力はTだけであり、抗力Fはその作用点が動かず、仕事をすることができないので、③と④を仕事から導くのは誤りだという。それなら 円柱の並進運動や回転運動のエネルギーをどのようにして導くかを示すべきである。
編集委員会は「運動量や角運動量を運動方程式から導くのは問題ないので、並進運動のエネルギー=運動量の2乗÷質量の2倍であり、回転運動のエネルギー=角運動量の2乗÷慣性モーメントの2倍であるから、その公式を丸暗記しておいて、並進と回転の運動量から、それぞれのエネルギーを求めよ」と宣うのだろうか。
編集委員会が仕事によって得られる唯一のエネルギーと称する⑤円柱の力学的エネルギーを、③、④の和として求めなくても、運動方程式(1)と(2)式から先に抗力Fを消去して求めることもできよう。つまり、(1)式と(2)式から、先に抗力Fを消去すると、
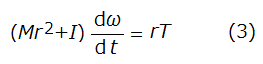
となる。(3)式にωを乗じてtで積分すれば、抗力Fのする仕事を考えなくても、Tのする仕事だけで⑤を導くことができる。図1の円柱の転がり運動では、円柱は重心のまわりに回転しているのではなく、地面との接点Pのまわりに回転しながらPが動くと見なすのである。それは、一見、抗力のする仕事を回避した素晴らしい考えのように思えるが、(1)と(2)からなる連立方程式と(3)式とは等価ではない。(3)式は抗力Fを消去した結果、もはや図1に対する運動方程式ではなく、次の図2のような固定された鉛直軸のまわりの回転運動にすり替わっている。
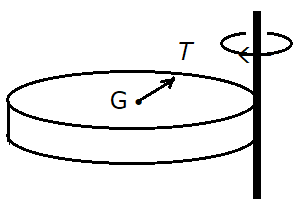
図1の転がり運動に対してP点は動かないが、転がり運動を並進運動と回転運動の和と考えたとき、P点は並進運動に対しては右方向に速さvで動き、回転運動に対しては左方向に同じ速さで動いている。しかし、図2の回転運動では、円柱は回転軸から抗力を受けるが、その抗力は運動方程式(3)には現れず仕事もしない。(1)と(2)の連立方程式で表される図1の転がり運動は二つの運動が重なった運動であり、単一の運動方程式で表される図2の回転運動とは明らかに異なる運動であり、両者を混同させてはならない。
編集委員会は、運動方程式など必要ない、数学も必要ないと考えているのだろうか。運動方程式に頼らずに説明することは重要だが、運動方程式に反した説明は本末転倒である。抗力は、その作用点が動かないので、外部から系にエネルギーを供給することはできないが、抗力が同時にする正と負の仕事によって力学的エネルギーが系内の運動形態に正しく配分されることは、(1)(2)式から、数学的に極めて自然に導かれることである。
図1の円柱の転がり運動は大学初年次レベルの問題であり、ニュートン力学が正しい限り、そこに疑義を挟む余地はない。高校物理教科書や大学初年次の物理教科書に記述されている仕事の定義を、仕事の対象を質点に限定した「初心者向けの仕事の定義」だとして、抗力が仕事をすることに頑迷に反対し続ける編集委員会は、ニュートン力学を否定したいのだろうか。定義する意義は物事を他と明確に区別するためにある。初心者向けの曖昧な定義など、定義の意味をなさない。編集委員会は、その主張が最初から破綻していることに気づくべきである。
言いたいことは、まだまだ山ほどあるが、血圧が高くなりそうなので、今回はこのへんで。次回、抗力のする正負同時一対の仕事Ⅱでは、動力源が系内に存在する場合について述べる。

コメント