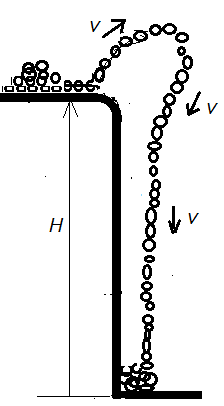
鎖の噴水のページの図4のように机の端のコーナーを滑り落ちるとき、鎖に遠心力が働き、鎖の流れが上に膨らむ。このとき、鎖の任意の「一粒」に働く力は、その粒に働く重力、先行する粒から受ける力、後続の粒子から受ける力である。任意の一粒に働く、それら全ての力の合力をFTとする。もし、途中に静止している障害物があれば、その障害物から受ける抗力もFTに含めるとする。机の上の鎖の塊から引き出された鎖の速さvと段差Hの間には、v2=gH…‥(3)が成り立ち、鎖の速さは段差Hで決まる。
鎖の速度ベクトルvとすると、(3)式は、v・v=gH、これを時間で微分することにより、v・dv/dt=0、鎖に沿った距離をsとすると、dv/dt=(ds/dt)(dθ/ds)(dv/dθ)。ここで、図5のようにθは、軌道曲線の接線を、基準線から測った角度、eを接線方向の単位ベクトル、nを内向き法線方向の単位ベクトル、rを曲線の曲率半径とすと、ベクトル解析から、de/dθ=n、dn/dθ=-eである。v=ve、であるから、加速度は法線方向のみとなり、dv/dt=(v2/r)nとなる。
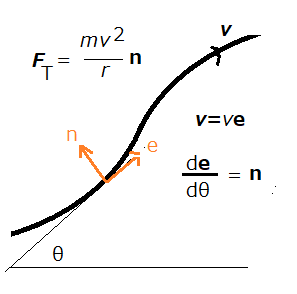
鎖の粒の質量をmとすると、運動方程式は、FT =(mv2/r)n…‥(4)となる。(4)式は鎖の粒の運動方程式でであるが、向心力FTと遠心力mv2/rのつりあいと考えることもできる。最初、図3(「鎖の噴水」のページ)のように机の面に沿って落下する場合、曲がり角で、遠心力が向心力より大きく、鎖は立ち上がり、両者が釣り合うと図4のような定常状態が実現される。
FTは、鎖の粒にその運動方向と常に垂直で、軌道曲線の内向き法線方向に働く。鎖の直線部分では、FT=0である。数珠つなぎされた鎖の粒は、先行する粒によって決められた「見えないレール」から内向き法線方向の抗力FTを受けながら運動するかのよう振る舞う。つまり、FTは「レール」に沿って等速曲線運動をする鎖の粒にいつも向心力として働く。 塊から、鎖の粒が引き出されるときと、鎖が床に衝突するときに生じる非弾性衝突によって鎖の粒の運動の速さが一定になるようにコントロールされているため、定常的な鎖の流れが実現され、粒子が均一であれば、どの粒子も先行する粒子の運動方程式と運動とを踏襲し、さらに後続に受け継がれていく。鎖の各粒は等速曲線運動をするが同じ曲線に沿って動くので、その形状は保たれる。
この問題をまともに、多粒子からなる系の運動方程式をつくって解こうとすると極めて難解となろう。しかし、その困難を迂回することによって初等力学で理解できよう。この問題を考えるにあたり、夏目雄平氏とのオンラインでの議論、村里英明氏のニュートンビーズに関するyoutubeの多くの実験が大変参考になった。改めてfacebook友達の両氏に深く感謝したい。
虫は窓から逃げようとして、何度もくりかえしくりかえしガラスにぶつかり、自分がもと入ってきた開いている隣の窓からでようとはしない。人間はもっと賢明に行動しうるか、あるいは少なくとも賢明に行動できるはずである。人間がすぐれているのは直接にはこえ難い障害物を迂回することを知っているということである。 ポリア(柿内賢信訳:≪いかにして問題をとくか≫
大学に入学して最初に受けた物理学講義の教科書、柿内賢信著、物理学(1959年丸善)の序文に引用されていたが、学生時代に一番印象に残った言葉である。
話は異なるが、抗力と仕事の問題も固定観念に囚われ、抗力は作用点が動かないので、一切仕事をしないと考えたら、車が道路を走るというありふれた現象さえも永遠に説明できないのではないだろうか。
ニュートンビーズの立ち上がる仕組み
上記の説明を一部訂正します。実際に実験をすると、図4において、鎖が立ち上がるのは机の端ではなく、鎖が一塊になっているところから立ち上がります。鎖の塊を机の端から離して実験をしてみました。初期条件として、鎖が静止した状態(鎖の噴水:図3)から実験を始めれば、机の上では水平運動しか考えられないのに、なぜ、立ち上がって鎖が位置エネルギーを持つのかよくわかりません。
これは、歳差運動をしている独楽が床から摩擦力を受け、摩擦力のジャイロ効果で独楽の軸が立ち上がり、回転の運動エネルギーが位置エネルギーになって独楽が眠り独楽の状態になるのと、似ていますが、鎖の場合も水平方向の運動エネルギーが位置エネルギーになる仕組みが存在しているかも知れません。

コメント
図4のように机の上に置かれた鎖では机より上には上がらないでしょう。図は間違いではないでしょうか。コップに入れた鎖は上向きに引っ張られますから慣性で図のようになりますが。
落差Hが充分大きければ、水平方向から下方に向きを変える時の遠心力で立ち上がると思います。スピードスケートの選手がコーナーを曲がるとき遠心力を受けるのと一緒です。ただし、鎖が台の上に一列に並んでいる場合は段差があっても立ち上がらず速さを増しながら落下するだけだと思います。台の上で鎖が一塊になっていることが重要です。立ち上がって定常状態ができると、空中の鎖の形も保存されます。鎖の塊から鎖の粒が引き出されるときの非弾性衝突によって鎖の速度が時間的にも空間的にも一定になることで起きる現象だと思います。私も動画しか見たことはありませんが、フェイスブックの友達がいろんな条件でニュートンビーズの実験をしていますので、その動画をご覧になることをお勧めします。
原 宣一 様
その後、実験をしましたら、机の上に置いた場合も立ち上がりました。ただし、立ち上がる場所は机の端ではなく、鎖が一塊になっている箇所から立ち上がりました。最初静止した状態から鎖を落とし始めても上向きの運動が生じるのが極めて不思議です。